3.2. Щокові дробарки

Щокову дробарку вперше запропону­вав американський інженер Дж. Блек у 1858 р. її кінематика істотно не зміни­лася до цього часу. Основними робочи­ми елементами дробарки є дві плити — щоки, одна з яких, як правило, нерухома (рис. 3.3). Матеріал подрібнюється зав­дяки періодичному зближенню дробиль­них щік. Вивантажується матеріал із дро­барки під дією гравітаційних сил при від­даленні щік.

Щокова дробарка має такі основні роз­міри: ширину вхідного отвору В; довжи­ну камери подрібнення L; висоту робочої камери нерухомої щоки Н; мінімальний розмір камери подрібнення в нижній ча­стині l ; хід щоки S.

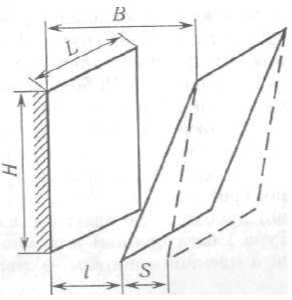
Типорозмір дробарки визначається шириною В, за якою оцінюють максималь­но можливу крупність кусків, що подріб­нюються. Максимальний діаметр беруть

D_max = 0,85 В. Існують такі залежності між висотою H , ходом S і шириною В:

Н= (2,0...2,5)B; S= (0,03...0,04)B (3.11).

Ці залежності можна використати при проектуванні дробарок. Індексація дробарок має літерну (вид дробарки) та циф­рову (розміри вхідного отвору) частини. Наприклад, дробарка ЩКП 900 х 1200 означає: щокова (Щ) крупного (К) по­дрібнення (П) з розмірами вхідного отво­ру 900 (В) па 1200 (І) мм. Найпоши­реніші дев'ять типорозмірів дробарок. Вагомою ознакою дробарок є їхня класи­фікація за характером хитання рухомої щоки. За цією ознакою щокові дробарки поділяють на дробарки з простим і склад­ним хитанням щоки.

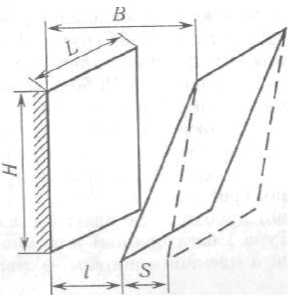
Рис. 3.3. Геометричні розміри дробарки

Рис. 3.4. Щокова дробарка з простим хитанням щоки:

а - конструкція; б - схема; в - схема розміщення плит

Дробарка з простим хитанням щоки (рис. 3.4, а, 6) складається із звар­ного корпусу 1, в якому на підшийниках установлений ексцентриковий вал 7 з підвищеним на ньому шатуном 8. Нижній кінець шатуна має спеціальні гнізда, в які вільно вставлені кінці розпірних плит 12 і 13. Протилежний кінець розпірної пли­ти 13 встановлений у гніздо рухомої щоки яку підвішено на осі 5. Кінець плити 12 впирається в клиновий упор регульо­ваного пристрою 9. Тяга 11 і пружина 10 забезпечують зворотний рух рухомої щоки і утримують від випадання розпірні плити. До нерухомої 2 і рухомої 3 щік прикріплюють дробильні плити 4 з верти­кальним рифленням. Робочі поверхні дробильних плит і бокові стінки корпусу дробарки утворюють камеру подрібнення.

Дробильні плити встановлюють так, щоб виступи однієї були навпроти запа­дин іншої (рис. 3.4, в).

Привід дробарки складається з елек­тродвигуна і багаторядної клинопасової передачі з масивним шківом — махови­ком 6.

Працює дробарка так. При обертанні ексцентрикового вала шатун здійснює зворотно-поступальні рухи у вертикальній площині, а рухома щока приводиться в хиткий, подібно до маятника, рух, тобто траєкторія руху точок рухомої щоки є частиною дуги кола. За один оберт екс­центрикового вала рухома щока, набли­жаючись до нерухомої, здійснює робочий хід подрібнення матеріалу, а при відда­ленні від нерухомої — холостий хід, під час якого подрібнений матеріал випадає крізь вихідну щілину.

Для забезпечення пуску дробарок, а та­кож пуску під завалом у нових конструк­ціях застосовують допоміжний привід (рис. 3.5). Він складається з електродви­гуна малої потужності 4, зубчастого ре­дуктора 3 з великим передаточним числом, обгінної муфти 2, з'єднаної з валом голов­ного двигуна 1. Пуск дробарки здійсню­ється допоміжним приводом. Після цьо­го вмикається головний двигун, а допо­міжний — автоматично вимикається.

Режим роботи дробарки змінюється регулюванням вихідної щілини за допомо­гою клинового чи іншого за конструкцією регулювального пристрою. Вихідну щіли­ну вимірюють між вершиною та запади­ною дробильних плит у момент найбільшого віддалення рухомої щоки. Ширина вихідної щілини для дробарок середньо­го подрібнення становить 40... 120 мм і для дробарок крупного — 100...250 мм. Як зазначалося (див. табл. 3.1), для щоко­вих дробарок з простим хитанням щоки найхарактернішим видом руйнування є роздавлювання і розколювання. Тому їх застосовують для крупного та середньо­го подрібнення твердих порід па пер­винній стадії подрібнення.

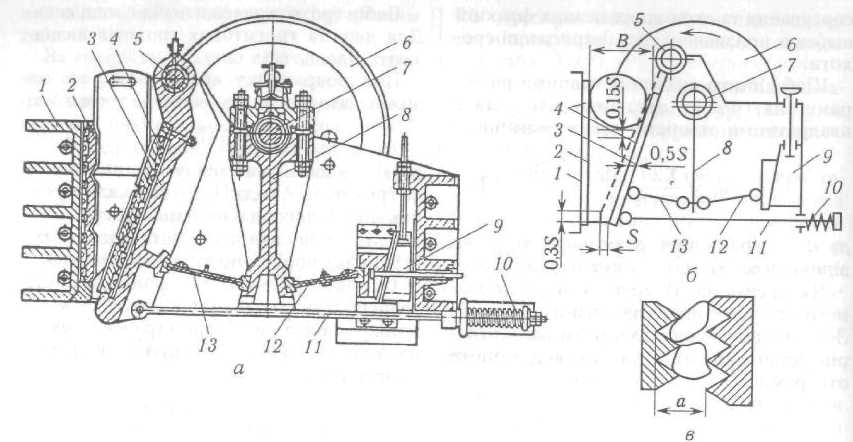
Дробарка зі складним хитанням щоки (рис. 3.6, а, б) за конструкцією простіша від дробарки з простим хитан­ням і має меншу масу.

У дробарці немає шатуна, а рухома щока 1 прикріплена безпосередньо до ексцентричної частини привідного вала 2. У нижній частині щока з'єднана розпір­ною плитою 5 з маточиною машини через клиновий регулювальний механізм 4. Дробарка має також замикальний при­стрій 3.

У такій дробарці траєкторія хитання рухомої щоки — замкнена еліптична кри­ва, з мінімальною різницею осей еліпса у верхній частині щоки і максимальною — у нижній. Зміна характеру хитання ру­хомої щоки змінює схему навантажень на матеріал, який руйнується під дією стис­кальних і зсувних сил. Одночасна дія зсувних сил інтенсифікує робочий про­цес. Окрім того, наявність дотичних сил, які діють на подрібнюваний матеріал, сприяє його вивантаженню.

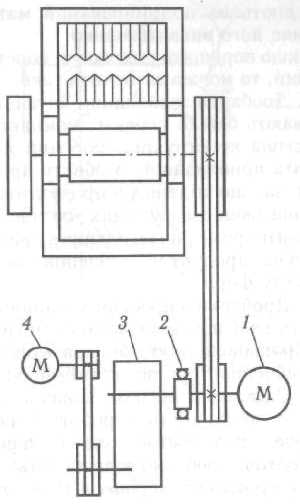
Рис. 3.5. Схема допоміжного приводу

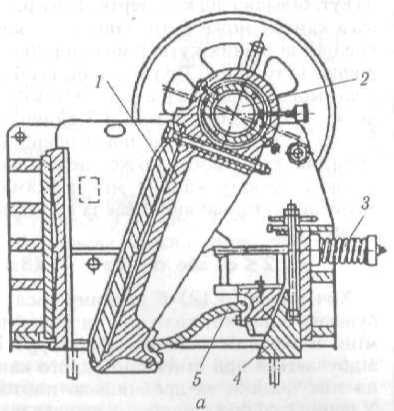
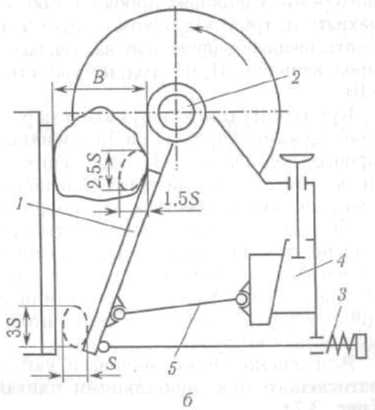
Рис. 3.6. Щокова дробарка зі складним хитанням щоки:

а — конструкція; б — схема

Якщо порівняти розглянуті конструкції машин, то можна зазначити таке.

Дробарки зі складним хитанням що­ки мають багато переваг: компактніша і простіша конструкція; робочий хід ста­новить приблизно 4/5 оберту привідно­го вала, що підвищує продуктивність і зрівноваженість рухомих частин; менші габаритні розміри і потужність привідного двигуна; продукт подрібнення має більш округлу форму.

2. Дробарки з простим хитанням щоки мають свої переваги: менше спрацюван­ня броньових плит, більша можливість подрібнення крупних кусків породи.

3. Загальний недолік щокових дроба­рок — циклічність у роботі (наявність робочого та холостого ходів). Окрім цьо­го, щокові дробарки відрізняються знач­ною енергоємністю процесу. При мінімаль­ній ширині вихідної щілини питома по­тужність дробарок із простим хитанням щоки становить 1,2.. .4,б кВт/ (м³ * год) і зі складним — 0,9...4,6 кВт/(м³ * год), в 2 — 4 рази перевищує енергоємність дро­барок інших типів.

Розрахунок основних параметрів щокових дробарок. Параметри механіч­ного режиму щокових дробарок такі: кут захвату а, град; хід рухомої щоки 5 мм; кутова швидкість привідного і продуктивність П, м³/год; потужність Р, кВт.

Кут захвату а між нерухомою та рухо­мою щоками впливає па інтенсивність процесу подрібнення. За підвищених зна­чень кута захвату матеріал, що подріб­нюється, виштовхується із камери по­дрібнення, за малих — зменшується сту­пінь подрібнення матеріалу і збільшуєть­ся висота дробарки. Отже, існує раціо­нальне значення кута, за якого камінь на­дійно утримуватиметься і не виштовху­ватиметься вгору.

Розглянемо умову рівноваги каменя, затисненого між дробильними плитами (рис. 3.7).

Вважатимемо, що камінь має форму кулі. У точках А і В дотику каменя дробильними

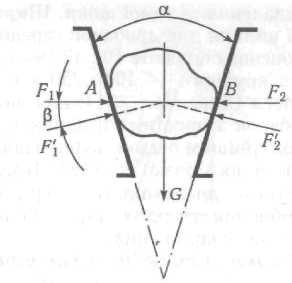
Рис. 3.7. Схема для визначення кута захвату

плитами на нього діють нор­мальні сили реакції і сили тертя. Позна­чимо F₁ — рівнодійну сил, прикладених до каменя в точці А, і F₂ — рівнодійну сил, прикладених у точці В. Оскільки на камінь більше ніякі сили не діють (ва­гою каменя G через її малість порівняно із силами F₁ і F₂ нехтуємо), рівновага каменя може бути лише тоді, коли сили

F₁ і F₂ однакові за значенням й напрям­лені назустріч одна одній по лінії АВ, що

перпендикулярна до бісектриси кута а з іншого боку, рівнодійна сил нормаль­ної реакції і тертя не може відхилятися кут, більший від кута тертя. Тому рівно­вага каменя може бути лише тоді, коли кожний із рівних кутів Р менший або до­рівнює куту тертя. Таким чином, необхід­ною умовою рівноваги є залежність  < , де  — кут тертя. З рис. 3.7 видно, що Р = /2 як кут із взаємно перпендику­лярними сторонами. Отже, необхідною умовою захвату каменя між щоками є значення кута, що випливає із співвідно­шення

/2 <  або < 2. (3.12)

Хоч умова (3.12) й витримується, та бувають випадки, коли той чи інший ка­мінь може виштовхнутися нагору. Це відбувається при стисканні одного каме­ня між іншими та дробильною плитою. У цьому разі фактичний кут захвату може виявитися значно більшим від кута між дробильними плитами. Розрахункові значення кута 20...25°, а зважаючи па мож­ливі реальні умови подрібнення, кут змен­шують до 18... 20°.

Хід рухомої щоки S тобто значення ходу стискання матеріалу в камері под­рібнення для забезпечення руйнування каменя, визначають із умови

S > еD, (3.13)

де e = _ст /Е — відносний стиск (_ст - напруження на стиск; Е — модуль пруж­ності); D — розмір куска. Однак через те, що подрібнені куски мають невизначену форму й контактують з дробильни­ми плитами не площинами, а точками, хід має бути більшим, ніж за умовою (3.13). Тому на практиці застосовують емпіричні формули, отримані експериментально. Для дробарок з простим хитанням рухо­мої щоки

S_B = (0,01. ..0,03)В;

(3.14)

S_H = 8 + 0,26 b,

Звідси для дробарок зі складним рухом

S_B = (0,06. ..0,03)В;

(3.15)

S_H = 7 + 0,10 b,

де S_B, S_H — хід відповідно у верхній і нижній точках рухомої щоки _; b - макси­мальний розмір вихідної щілини, мм.

Кутову швидкість ексцентрикового ва­ла визначають із умови, що за чаc відхи­лення t_від рухомої щоки на відстань S під дією власної ваги за час t_вип випада­ють куски подрібненого матеріалу, що мають висоту h (рис. 3.8).

Цю умову можна записати у такому вигляді:

t_від  t_вип (3.16)

При кутовій швидкості , рад/с, час відхилення рухомої щоки t_від = /. Якщо камера подрібнення глибока, то можна припустити, що щока відходить від початкового положення у нове положення S_H паралельно початковому положенню. Тоді з вихідного отвору дро­барки випадає призма подрібненого ма­теріалу заввишки h = S_H / tg .

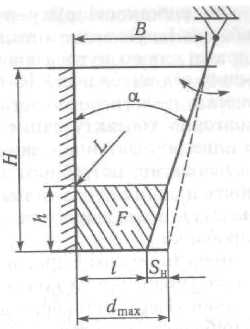
Ряс. 3,8. Схема для позначення кутової швидкості Ексцентрикового вала та продуктив­ності дробарки

Шлях, який пройшла призма за час t_вип можна знайти з відомого закону вільного падіння

h = . Звідси t_вип =

Використавши умову (3.16) , матимемо

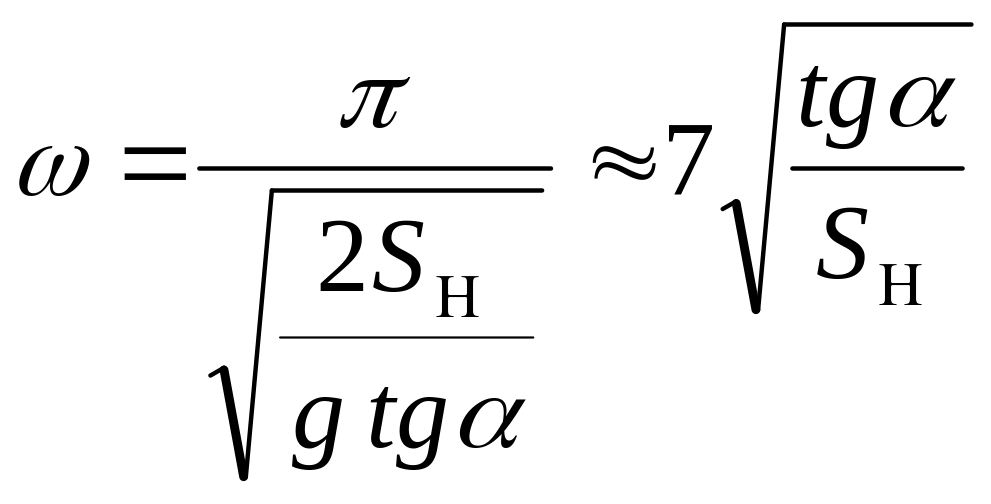(3.17)

При раціональному значенні кута  = 20° оптимальна кутова швидкість при­відного вала

(3.18)

Ураховуючи зниження швидкості ви­падання матеріалу із камери подрібнен­ня за рахунок тертя по дробильній щоці (у межах 5... 10 ^%), формула (3.18) набе­ре вигляду, рад/с,

(3.19)

Отже, для швидкості руху рухомої щоки дробарки існує певне оптимальне число. Справді, якщо кутова швидкість буде більшою від залежності (3.19), то кусок матеріалу не встигне випасти з дро­барки і повторно контактуватиме з дро­бильними плитами. За умови, що кутова швидкість менша від потрібного значен­ня, швидкість падіння куска гальмувати­меться плитами і, отже, знизиться продук­тивність дробарки.

Продуктивність щокової дробарки ви­значається за умови, що за кожен вихід щоки або один оберт головного вала із камери подрібнення вивантажується гото­вий продукт у вигляді призми трапецоїд­ного перерізу, об'єм якої V = FL (F — площа перерізу призми, що випадає з дробарки, м²; l довжина камери подрібнення дробарки, м).

Визначаючи площу, беремо такі самі вихідні дані, що і в попередньому випад­ку (див. рис. 3.8): щока віддаляється паралельно своєму початковому положен­ню, а висота призми h = S/tga.

Отже, площа перерізу призми

F=

де e—ширина вихідної щілини. Об'єм призми матеріалу, що випадає:

V =FL =

У разі n повних хитань рухомої щоки за 1 с продуктивність дробарки, м³/год:

П = 360ОnVk_р = (3.20)

де k_р — коефіцієнт розпушення маси ма­теріалу, який випав із вихідної щілини.

Якщо взяти rf_max = e + S, d_min = e , а середній розмір продукту подрібнення

d = d_ср = (3.21)

Слід пам'ятати, що продуктивність дро­барок, визначена за формулами (3.20) і (3.21), може значно відрізнятися від фак­тичних даних, оскільки вони не врахову­ють вилив інтенсивності й рівномірності живлення машини, форми та розмірів дробильних плит та їх спрацювання. Крім того, певну невизначеність вносить кое­фіцієнт k який змінюється в широких межах (k_p =0,30...0,65).

Потужність електродвигуна щокової дробарки можна встановити, використо­вуючи загальний підхід до визначення енергії, що відповідає об'ємній теорії по­дрібнення. Згідно з виразом роботи

А = V потрібно знати різницю об'ємів вхідного матеріалу V₁, та готового продукту

V₂ , тобто V = V₁-V₂ .

За об'єм матеріалу, що надходить у дробарку, пропонується брати кілька кусків, що мають форму кулі діаметром D який відповідає ширині В вхідного отвору. При довжині щілини L загальний об'єм кусків, що подрібнюватимуться,

V =

За об'єм готового продукту також бе­руть кілька кусків, що мають форму кулі діаметром d :

V₂ =

Тоді різниця об'ємів

V=V₁-V₂=

а робота, витрачена на подрібнення

А= =

Отже, потужність електродвигуна, яка потрібна для подрібнення матеріалу при врахуванні виразу роботи.

Р_др = (3.22)

Потужність, визначена за формулою (3.22), матиме завищене значення, що по­яснюється ідеалізованою схемою живлен­ня, а також урахуванням при руйнуванні матеріалу лише напруження від роздав­лювання. Справді, розраховуючи об'єми, вважають, що у вхідний отвір дробарки потраплятиме суцільний ряд кусків мак­симально можливого розміру, чого не бу­ває в реальних умовах. Окрім цього, при подрібненні, як уже зазначалося, поряд з роздавлюванням відбуваються деформації згину, розколювання тощо.

Потужність можна визначити й іншим способом. Так, на основі опрацювання статистичних даних щодо вимірювання енергії пропонуються такі емпіричні фор­мули:

• для дробарок крупного подрібнення

Р = (3.23)

• для дробарок середнього подрібнення

Р = (0,007...0,01)В; (3.24)

• для дробарок дрібного подрібнення

Р = (3.25)

У цих формулах ширину і довжину вхідного отвору наведено в сантиметрах.

Потужність, кВт, можна визначити, ви­користовуючи значення середньої рівнодійної сили подрібнення F_др :

Р = (3.26)

де S_f — хід щоки у точці прикладення сили F_др.

Практичне використання формули по­требує знання сили F_дp і S_f.

Щоб визначити зусилля в елементах дробарок, насамперед знаходять рівнодійну сил подрібнення та місце її прикладення. Під час робочого ходу рухо­мої щоки зусилля подрібнення досягає максимального значення при найбільшо­му зближенні щік. Експерименти засвід­чують, що при подрібненні граніту з гра­ницею міцності до 300 МПа максимальне навантаження на дробильну щоку q = 2,7 МПа. Це навантаження розподі­ляється рівномірно на всю площину пли­ти. Отже, максимальне зусилля

F_max = qLH=2.7 10⁵ LH (3.27)

Ураховуючи умови тертя на поверхні рухомої щоки, силу F_max наближено мож­на взяти за напрямлену перпендикуляр­но до нерухомої щоки і прикладену на половині висоти камери подрібнення (рис. 3.9, а).

Процес подрібнення є дуже нестабіль­ним. Тому для розрахунків елементів дробарки на міцність розрахункове зусил­ля F беруть на 50 % більшим від F_max :

F = 1.5F_max (3.28)

Напрямлення сили F таке саме, як і сили F_max. За розрахованим зусиллям F можна аналітичним або графічним спо­собом знайти зусилля в усіх робочих еле­ментах дробарки і розрахувати їх на міцність. Для дробарки з простим хитан­ням рухомої щоки(рис. 3.9, а) розрахун­ки виконують у такій послідовності.

1. Знаходять кут 5 як 8 = 90 -  ( —кут між розпірною плитою і шатуном, 80°<<90°).

2. Визначають кут у між силою в роз­пірній плиті та її проекцією на рухому щоку:

 =- , де  - кут між щоками (задається за умовою задачі).

3. Складають рівняння моментів відносно осі підвісу рухомої щоки О:

Звідси

T₁ =

4. Знаходять зусилля в розпірній плиті:

T = .

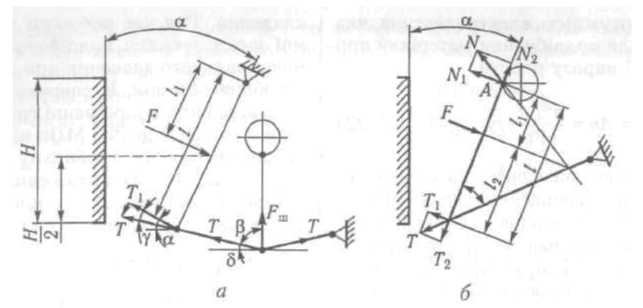
Рис. 3.9. Схема сил в елементах конструкції щокової дробарки :

а - із простим хитанням щоки; 6 — зі складним хитанням щоки

5. Визначають зусилля в шатуні:

F_щ = 2Т cоs. (3.29)

Із (3.29) випливає, що T = .

При = 90° Т—> 0. Тому кут  беруть у межах 80°<<90°.

6. Розраховують силу, що діє на не ру­хому щоку:

F_H = F cos 

У дробарках зі складним хитанням щоки (рис. 3.9, б) крім зусилля F на ру­хому щоку діють сили N — у точці А підвісу щоки па привідному валу і Т — у точці В з'єднання щоки з розпірною пли­тою. Ці сили розкладаються на складові N₁ і T₁, нормальні до поверхні щоки, та N₂ i T₂ , що діють по довжині щоки. Зна­чення А і В визначають з умов рівноваги сил системи, що діють на щоку відносно точок А і В, М_А = 0; Т₁l = Т₁l₁ звідки T₁= ; ; N₁l = Fl₂; N₁= ;

де l₁ і l₂ — відстань від точки прикла­дення сили F до точок А і В відповідно. Складова T₂ чисельно дорівнює N₂ і визначається за формулою

T₂ = T₁tg  = F ,

де  — кут між рухомою щокою і розпір­ною плитою, град.

Зусилля, що діє у розпірній плиті,

T = .

Зусилля, що діє на привідний вал і його підшийники,

N = .

Для розрахунку елементів дробарок па міцність використовують загальноприй­няті методи з урахуванням особливостей їх навантаження. Так, ексцентриковий вал розраховують на згин та кручення і пере­віряють на міцність до втоми.

Розпірну плиту розраховують на збіль­шене допустиме навантаження на стиск чи згин залежно від конструкції плити.

Рухому щоку розраховують на розтяг, згин і стиск.

Зварну чи литу станину щокової дро­барки розраховують як прямокутну раму, в якій па поперечні стінки зсередини діє рівномірно розподілене навантаження.

Шатун розраховують па стиск і розтяг.

Розрахунок маховика зводиться до визначення його геометричних розмірів і маси. В основу розрахунків покладено ро­боту, яку викопують двигун і маховик.

Розглянемо роботу дробарки, викорис­товуючи для цього закон зміни зусилля подрібнення за один оберт ексцентрико­вого вала (рис. 3.10, а).

Зусилля виникає при повороті ексцен­трикового вала S на  = 30.. .45°, що пояс­нюється перекомпонуванням каменя в камері (рис. 3.10, б). Далі зусилля швид­ко збільшується, досягаючи максимально­го значення при куті повороту  = 180° (точка А). Зміна знака сил тертя при подальшому повороті виражається орди­натою АВ, потім зусилля падає до нуля приблизно на половині холостого ходу. Якщо при робочому ходу зусилля F на­прямлене проти руху щоки, то при хо­лостому — в бік руху щоки. Завдя­ки відновленню пружних деформацій при холостому ходу частина енергії, витраче­ної при робочому ходу, повертається. Тоб­то при холостому ходу енергія акуму­люється і віддається при робочому, що дає змогу зменшити потужність двигуна. Загальна енергія па подрібнення вира­жається площею діаграми. Якщо припус­тити, що робота подрібнення, Дж, дорів­нює площі трикутника OAD, то

А_др=

де S₁ — хід рухомої щоки в точці прикла­дення сили F_max .

Припустімо також, що робота махови­ка, Дж, дорівнює роботі двигуна, тобто

А_мах = А_дв =

З другого боку, роботу маховика мож­на знайти за виразом

А=(mv²_max/2)-(mv²_min/2), (3.30)

де m — маса маховика; v — лінійна швид­кість маховика: v = R (_max - кутова швидкість, яка в робочому режимі зміню­ється від _mах до _min ; R - маховика). Тоді вираз (3.30) набере ви­гляду

A_max = mR^{2 =} I ^, (3.31)

де момент інерції I = mR² . Якщо подати квадрати швидкостей як

²_max-²_min = (_max-_min)(_max+_min)

і врахувати, що коливання кутової швид­кості залежить від ступеня нерівномір­ності обертання маховика

,

де

,

Рис. 3.10. Діаграма зміни зусилля подрібнення

за один оберт ексцентрикового вала

то

A_max = I_cp (3.32)

Для дробарок беруть  = 0,015...0,035.

З другого боку, А_мах = А_дв = . Із рівняння (3.31) момент інерції

І = ,

де  =0,65...0,85 - ККД дробарки.

Оскільки швидкість у реальних конст­рукціях дробарок v = nD_n = 20...30 м/с, кінцеві розрахунки маховика зводять до такого:

1. Визначають діаметр маховика

.

2. Із залежності (3.32) визначають момент інерції маховика

3. Ураховуючи, що І = 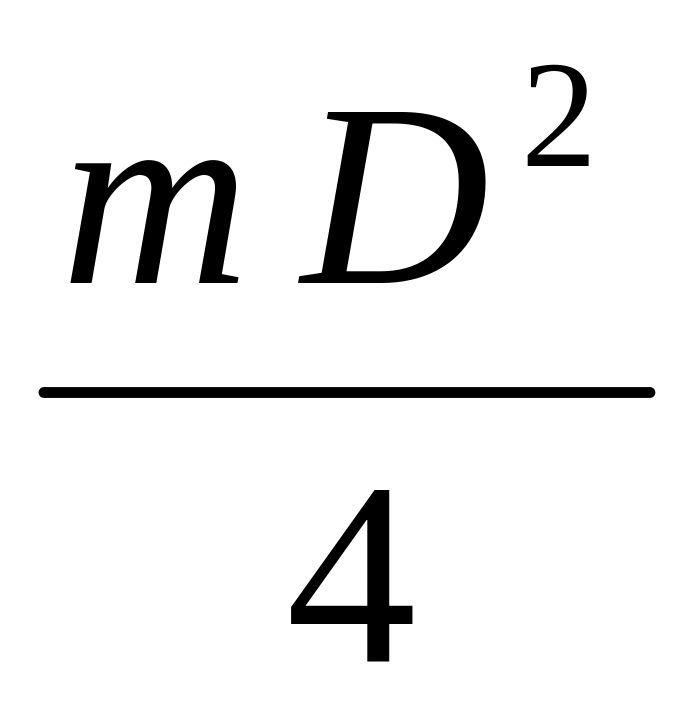, встанов­люють масу маховика:

(3.33)

Отже, використання маховика дає змо­гу забезпечити плавність ходу і зрівнова­ження інерційних сил, що виникають, а та­кож певного зменшення потужності під час виконання роботи подрібнення породи.