Синтез аналогових активних і пасивних фільтрів в micro-cap 8
Програма Micro-Cap 8 фірми Spectrum Software дуже зручна для первинного освоєння моделювання схемотехніки електронних схем. Найбільшого поширення вона може набути при навчанні студентів. Але і для інженерно-технічних працівників, що займаються проектуванням радіоелектронної апаратури, багато з можливостей цієї програми мають велике практичне значення. У цій статті піде мова про функцію синтезу схеми фільтрів.
Програма Micro-Cap 8 (надалі - MC8) має функцію Filter Design, яка дозволяє синтезувати схеми фільтрів. По командах меню Design синтезуються аналогові активні і пасивні фільтри. Завдання на синтез передбачає вибір типу фільтру, введення характерних частот і коефіцієнта посилення фільтру. В результаті синтезу розраховується порядок фільтру при апроксимації його передавальної функції поліномами різного типу і таблиця нулів і полюсів окремих ланок фільтру. На закінчення розраховуються стандартні реалізації схем цих ланок, які записуються в окремі файли для подальшого використання.
Доступні два типи проекту фільтру - проект активного фільтру і проект пасивного фільтру. Обидві доступні з меню Design. Меню Design містить дві команди Active Filters і Passive Filters для синтезу активних і пасивних аналогових фільтрів. Обидві ці команди мають однотипні діалогові вікна.
Можна синтезувати наступні типи фільтрів :
Low pass - фільтр нижніх частот (ФНЧ);
High pass - фільтр верхніх частот (ФВЧ);
Bandpass - смуговий фільтр (ПФ);
Notch - режекторний фільтр (РФ);
Delay - фільтр, що забезпечує затримку.
Перші чотири типи фільтру характеризуються графіками Боде (АЧХ - амплітудно-частотна характеристика, ФЧХ - фазочастотна характеристика і залежність групового часу запізнювання від частоти) і можуть бути реалізовані у вигляді активних або пасивних фільтрів. Фільтри Delay характеризуються часом затримки і можуть бути реалізовані тільки у вигляді активного фільтру.
Залежно від типу апроксимуючого полінома передавальної функції доступні наступні типи фільтру:
Butterworth - фільтри Баттерворта;
Chebyshev - фільтри Чебишева;
Bessel - фільтри Бесселя;
Elliptic - еліптичні фільтри;
Inverse - Chebyshev - інверсні фільтри Чебишева.
Не усі ці апроксимуючі поліноми доступні для кожного типу фільтру. Апроксимуючий поліном Бесселя, наприклад, доступний тільки для фільтру Delay.
Схемні реалізації для активних фільтрів можуть бути різні для кожної ланки і включають:
Sallen - Key;
MFB;
Tow - Thomas;
Fleischer - Tow;
KHN;
Acker - Mossberg;
Tow - Thomas 2;
DABP (Dual Amplifier Band Pass).
Синтез активних фільтрів
Вибір команди Active Filters в меню Design відкриває діалогове вікно, показане на Рис. 1.
Діалогове вікно синтезу активних фільтрів(Рис. 1
)
Рис. 1. Діалогове вікно синтезу активних фільтрів (вкладка Design)
Це діалогове вікно має три основні вкладки:
Вкладка Design містить групи:
Type (тип) - дозволяє вибирати один з п'яти основних типів фільтрів :
o Low pass;
o High pass;
o Bandpass;
o Notch;
o Delay.
Response (частотна характеристика) - дозволяє вибирати математичну апроксимацію ідеального фільтру :
o Butterworth;
o Chebyshev;
o Bessel;
o Elliptic;
o Inverse - Chebyshev.
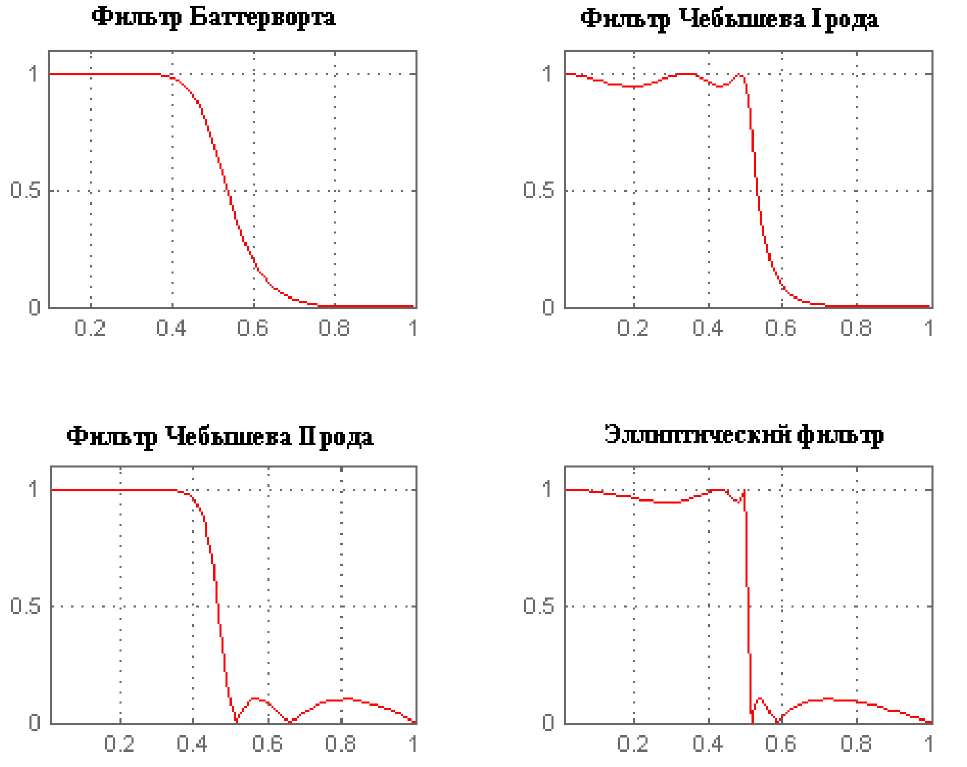
Різні частотні характеристики забезпечують різні компромісні співвідношення проекту. Фільтри Баттерворта вимагають збільшення числа ланок для отримання заданих технічних вимог, але мають постійну часову затримку в межах смуги пропускання. Фільтри Чебишева і інверсні фільтри Чебишева вимагають меншої кількості ланок, але мають більш яскраво виражену зміну часової затримки. Еліптичні фільтри вимагають найменшої кількості числа ланок, але мають найбільшу зміну затримки. Фільтри Бесселя є фільтрами нижніх частот з постійною затримкою і використовуються як елемент затримки. Число ланок для реалізації поточного проекту показується в полі Response праворуч від типу апроксимуючого полінома.
Specifications (технічні вимоги) - сюди вводять технічні вимоги до фільтру. Є два способи визначити фільтр: Mode 1 (режим 1) і Mode 2 (режим 2). У Mode 1 визначаються функціональні характеристики фільтру, подібні Passband Gain, Passband (Fc), Stopband (Fs) і Stopband Atten. (A). Тут визначається те, що необхідно, і програма обчислює число ланок, потрібних для досягнення цього, використовуючи вказану апроксимацію частотної характеристики. Режим Mode 2 дозволяє безпосередньо визначити основні значення параметрів проекту і число ланок фільтру.
Вікно Poles and Zeros (полюси і нулі) - показує числові значення полюсів, нулів і Qs поліноміальної частотної характеристики. Тут, по суті, показується математичний проект фільтру. Коли виконуються зміни в полях Type, Response або Specifications, програма перепроектує поліноміальні коефіцієнти і модифікує числа в цьому вікні. Якщо кнопки Bode, Step або Impulse були натиснуті, програма також перемальовує графіки. Які графіки Боде будуть показані, можна вибрати на панелі Options.
Графіки ідеалізуються, тому що вони засновані на стандартній поліноміальній формулі для вибраної частотної характеристики і обчислених або відредагованих значеннях F0, Q0 і QN. Такі характеристики можуть бути досягнуті тільки з ідеальними компонентами. Реальний фільтр, зроблений з реальних компонентів, поводитиметься дещо по -іншому. У реальності схема може бути створена на основі будь -якого операційного підсилювача (ідеального або реального) і з резисторів і конденсаторів, які точно рівні розрахунковим або вибрані із списку стандартних значень. Реальний операційний підсилювач і приблизні значення компонента можуть чинити сильний вплив на графіки частотних характеристик.
Зверніть увагу, що при редагуванні будь -якого параметра в полях Type, Response або Specifications програма повторно обчислює значення у вікні Poles and Zeros, змінюючи відредаговані значення.
Точна форма апроксимуючих поліномів для кожної ланки фільтру має вигляд:
Фільтри нижніх частот і затримки (Low Pass і Delay) :
. Butterworth F(U) = 1/(U2+U/Q0+1);
. Chebyshev F(U) = 1/(U2+UxW0/Q0+W02);
. Elliptic F(U2+UxW0/Q0+W02);
. Inv. Chebyshev F (U2+Ux W0I/Q0+W0I2).
Фільтр верхніх частот (High Pass) :
. Butterworth F(U) = U2/(U2+U/Q0+1);
. Chebyshev F(U) = U2/(U2+U/(W0xQ0)+ 1/W02);
. Elliptic F(U2+U/(W0xQ0)+ 1/W02);
. Inv. Chebyshev F(U2+U/(W0IxQ0)+1/W0I2).
Смуговий фільтр (Bandpass) :
. Butterworth F(U) = U/(U2+U/(W0xQ0)+1/W02);
. Chebyshev F(U) = U/(U2+U/(W0xQ0)+ 1/W02);
. Elliptic F(U2+U/(W0xQ0)+ 1/W02);
. Inv. Chebyshev F(U2+U/(W0IxQ0)+1/W0I2).
Режекторний фільтр (Notch) :
. Butterworth F(U2+U/(W0xQ0)+1/W02);
. Chebyshev F(U2+U/(W0xQ0)+1/W02);
. Elliptic F(U2+U/(W0xQ0)+ 1/W02);
. Inv. Chebyshev F(U2+U/(W0IxQ0)+1/W0I2) Тут: F - змінна частота; S = JW2WPIWF - комплексна частота; U = S/(2WPIWFC) = JWF/FC - нормалізована комплексна частота; F0 - місце розташування полюса в Гц; Q0 - значення добротності; FN - місце розташування нуля в Гц (тільки для еліптичних і фільтрів Чебишева); FC - частота Stopband для фільтрів нижніх частот, частота Passband для фільтрів верхніх частот або середня (центральна) частота для смугового і режекторного фільтрів (вказана середня частота може бути змінена небагато для створення симетричної смуги пропускання/режекції, наприклад, смуговий фільтр Баттерворта, використовуючи задану за умовчанням середню частоту 1000 і смугу пропускання 100, насправді буде спроектований з середньою частотою 998,75 Гц); FCI - частота Passband для фільтрів нижніх частот, частота Stopband для фільтрів верхніх частот; для смугового і режекторного фільтрів FCI = FC; W0 = F0/FC - нормалізована частота полюса; W0I = F0/FCI - нормалізована частота полюса для фільтру Inverse Chebyshev; WN = FN/FC - нормалізована частота нуля; WN = FN/FCI - нормалізована частота нуля для фільтру Inverse Chebyshev.
Вкладка Implementation (реалізація) дозволяє вирішувати, як здійснити проект фільтру (Рис. 2). Вона має декілька полів і вікон. Діалогове вікно синтезу активних фільтрів(Рис. 2)