8. Трехфазная цепь, соединенная треугольником при несимметричной нагрузке.
В случае несимметричной нагрузки
и симметрия векторных систем токов нарушается. Но в
любом случае система векторов фазных напряжений остается жесткой, а также всегда выполняется соотношение между линейными токами:
В случае обрыва линейного провода А-а при соединении треугольником фазы нагрузки ca и ab оказываются соединенными последовательно, их можно рассматривать как одно общее сопротивление
которое, как и сопротивление фазы bc, находится под напряжением Ubc.
Согласно второму закону Кирхгофа
но поскольку
то
Напряжения на фазах ca и ab:
Рассматривая abc как контур, получим соотношение:
Линейные токи определяются из уравнений первого закона Кирхгофа для узлов с и b, но теперь
При построении векторной диаграммы может оказаться полезным анализ отношения напряжений. Например, при симметричной нагрузке
и
т.е.
векторы
и
совпадают по фазе и по величине.
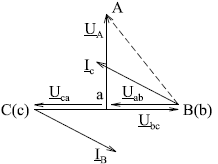
Напряжение в месте обрыва определяется следующим образом:
При несимметричной нагрузке отношение
является комплексным числом, значит, точка а находится вне отрезка bc. В случае обрыва фазы ab нагрузки для анализа электрического состояния цепи можно использовать полученные ранее соотношения между токами и напряжениями, учитывая, что
при
этом режимы работы остальных фаз не
нарушаются, изменяются лишь линейные
токи
и
Соотношения между токами с учетом
имеют вид:
Напряжение в месте
обрыва равно линейному напряжению
