4. Расчет трехфазных цепей

Расчет трехфазной цепи, соединенной звездой

Трехфазную цепь, соединенную звездой, удобнее всего рассчитать методом двух узлов. Вспомним, в чем состоит этот метод (он является частным случаем метода узловых потенциалов). Прежде всего, отметим, что этот метод применяется для цепей, состоящих из параллельно соединенных ветвей. Ток в каждой из ветвей может быть определен как отношение разности действующих в этой ветви ЭДС и межузлового напряжения к сопротивлению цепи. В свою очередь, межузловое напряжение определяется как эквивалентное напряжение, созданное источниками всех ветвей.

На рис. 7.5 изображена трехфазная цепь при соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы (Z_A ≠ Z_B ≠ Z_C )

Рис.7.5

Нейтральный провод имеет конечное сопротивление Z_N .

В схеме между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали.

Это напряжение определяется на основе следующих соображений. В соответствии с законом Ома для каждой ветви запишем

Преобразуя полученное соотношение, приходим к выражению для межузлового напряжения цепи в виде формулы (7.2)

(7.2)

Фазные токи определяются по формулам (в соответствии с законом Ома для активной ветви):

(7.3)

Ток в нейтральном проводе

(7.4)

Частные случаи.

1. Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению Z_A = Z_B = Z_C = R.

Узловое напряжение

,

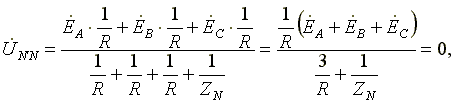потому что трехфазная система ЭДС симметрична:

.

Напряжения фаз нагрузки и генератора одинаковы:

Фазные токи одинаковы по величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует

Таким образом, в трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.

На рис. 7.6  изображена векторная диаграмма трехфазной цепи для симметричной нагрузки.

рис. 7.6

2. Нагрузка несимметричная,   R_A< R_B = R_C, но сопротивление нейтрального провода равно нулю:  Z_N = 0. Напряжение смещения нейтрали

Фазные напряжения нагрузки и генератора одинаковы

Фазные токи определяются по формулам

Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов. На  рис.  7.7  приведена векторная  диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления

Рис. 7.7

3. Нагрузка несимметричная, R_A< R_B = R_C, нейтральный провод отсутствует, т.е.

В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:

Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.

Из-за напряжения  смещения нейтрали фазные  напряжения нагрузки становятся неодинаковыми.

Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.

На рис. 7.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом.

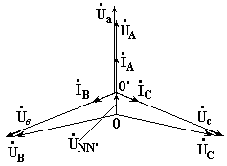
Рис. 7.8

Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми.

Трехфазная цепь, соединенная треугольником.

Соединение обмоток генератора или фаз приемника, при котором начало одной фазы соединяется с концом другой, образуя замкнутый контур, называется соединением треугольником (D). Таким образом, нагрузка включается между линейными проводами.

Начало фазы А источника питания соединяют с концом фазы В и точку соединения обозначают А. Далее соединяют точки В и Z (точка В) и точки С и X (точка С). Направления ЭДС приняты как и при рассмотрении схемы соединения звездой.

Подобным образом соединяют треугольником и фазы приемника, сопротивления которых обозначены двумя индексами, соответствующими началу и концу фазы.

По фазам приемника протекают фазные токи I_ab, I_bc, I_ca. Условно положительное направление фазных токов приемника принято от точки первого индекса к точке второго индекса. Условно положительное направление фазных напряжений U_ab, U_bc, U_ca совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов I_A, I_B , I_C принято от источника питания к приемнику.

Поскольку каждая фаза нагрузки включена между линейными проводами, т о линейное напряжение равно фазному напряжению: .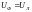

Комплексные токи в фазах нагрузки могут быть определены по закону Ома:

где

Комплексные токи в линейных проводах связаны с фазными токами первым законом Кирхгофа:

Итак, линейные токи при соединении треугольником равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.

Отсюда следует, что векторная сумма линейных токов равна нулю:

Система линейных-фазных напряжений при соединении треугольником образует такой же замкнутый треугольник, как и при соединении звездой.

Если нагрузка симметрична, то

и из полученных соотношений следует, что фазные токи нагрузки и линейные токи одинаковы:

а их векторы образуют симметричные системы.

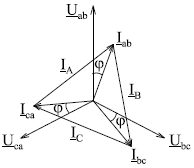
Из векторной диаграммы следует, что при симметричной нагрузке величины линейных и фазных токов связаны соотношением:

Расчет трехфазной цепи, соединенной треугольником

Для расчета трехфазной цепи, соединенной треугольником можно проводить на основе следующих подходов. Во-первых, можно использовать методы расчета, предназначенные специально для таких цепей. Во-вторых, можно преобразовать «треугольную» цепь в звезду и воспользоваться рассмотренным выше методом расчета «звездных» цепей