- •Однофазные электрические цепи переменного тока
- •2.1. Способы представления синусоидальных токов, напряжений, эдс
- •1. Аналитический способ
- •2. Временная диаграмма
- •3. Графоаналитический способ
- •4. Аналитический метод с использованием комплексных чисел
- •2.2. Действующее значение переменного тока и напряжения
- •2.4. Основные свойства простейших цепей переменного тока
- •1. Участок цепи, содержащий активноесопротивле-ние (рис. 2.6).
- •2. Участок цепи, содержащий идеальную индуктивность (рис 2.9)
- •3. Участок цепи, содержащий ёмкость (рис. 2.12)
- •2.5. Сопротивления в цепи переменного тока
- •2.6. Мощности в цепях переменного тока
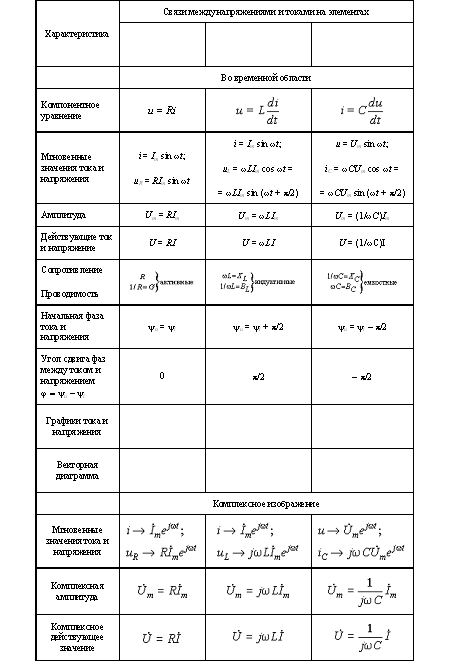
- •Элемент r (резистор)
- •2. Элемент l (индуктивность)
- •3. Элемент с (ёмкость)
- •2.7. Цепь с последовательным соединением элементов
- •2.8. Цепь с параллельным соединением элементов
- •3.5 Комплексные проводимости
- •3.6 Пассивный двухполюсник в цепи синусоидального тока
- •3.7. Мощности в цепях переменного тока
- •3.7.1 .Условие передачи максимальной мощности от источника энергии к приёмнику
- •2.9. Повышение коэффициента мощности в электрической цепи
- •2.10. Комплексный (символический) метод расчета цепей синусоидального тока
- •3.8 Комплексные частотные характеристики электрических цепей
3.8 Комплексные частотные характеристики электрических цепей
К ним относятся входные и передаточные функции, записанные в комплексной форме.
Входная комплексная функция цепи - это зависимость от частоты комплексного сопротивления:
![]() (3.43)
(3.43)
или комплексной проводимости:
![]() (3.44)
(3.44)
относительно двух выделенных выводов.
Пример 1.

Рисунок 3.12 - Электрическая схема для примера 1
Для данной схемы найдем комплексное входное сопротивление, его модуль и аргумент:
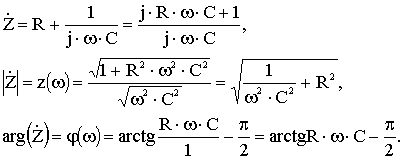 (3.45)
(3.45)
По полученным зависимостям строим соответствующие графики:


а) б)
а - модуль входной функции;
б - аргумент входной функции
Рисунок 3.13 - Частотные характеристики схемы примера 1
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.
Различают четыре вида передаточных функций:
1) передаточная функция по напряжению:
![]() ,
(3.46)
,
(3.46)
2) передаточная функция по току:
![]() ,
(3.47)
,
(3.47)
3) передаточное сопротивление:
![]() ,
(3.48)
,
(3.48)
4) передаточная проводимость:
![]() .
(3.49)
.
(3.49)
В общем виде передаточная функция:
![]() (3.50)
(3.50)
представляется в виде АЧХ - К(ω) и ФЧХ - φ(ω).
Пример 2.

Рисунок 3.14 - Электрическая схема для примера 2
Для данной схемы найдем передаточную функцию по напряжению, выразив её через отношение выходного комплексного напряжения к входному:
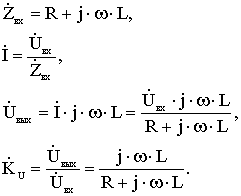 (3.51)
(3.51)
Находим АЧХ:
 .
(3.52)
.
(3.52)
Находим ФЧХ:
![]() .
(3.53)
.
(3.53)
По полученным функциональным зависимостям строим графики АЧХ и ФЧХ:


а) б)
а - модуль передаточной функции;
б - аргумент передаточной функции
Рисунок 3.15 - Частотные характеристики схемы примера 2
Связи между синусоидальными напряжениями и токами на элементах R, L, C