3.7.1 .Условие передачи максимальной мощности от источника энергии к приёмнику

Комплексные сопротивления внутреннего и внешнего участка цепи находятся следующим образом:

(3.39)

Мощность приёмника:

(3.40)

Отсюда при любом r_н мощность достигает наибольшего значения при x_н = - x_вн. В этом случае:

. (3.41)

Взяв от полученного выражения производную по r_н и приравняв её нулю найдем, что P имеет наибольшее значение при r_н = r_вн.

Таким образом, приёмник получает от источника наибольшую активную мощность, если его комплексное сопротивление является сопряжённым с комплексным внутренним сопротивлением источника:

, (3.42)

при этом η=0,5.

2.9. Повышение коэффициента мощности в электрической цепи

Активная мощность потребителя определена формулой

P = U I cos φ.

Величину cos φ здесь называют коэффициентом мощности. Ток в линии питающей потребителя с заданной мощностью Р равен

I = P / (Ucos). (2.51)

и будет тем больше, чем меньше cos . При этом возрастают потери в питающей линии. Для их снижения желательно увеличивать cos . Большинство потребителей имеет активно-индуктивную нагрузку. Увеличение cos  возможно путем компенсации индуктивной составляющей тока путем подключения параллельно нагрузке конденсатора (рис. 2.24).

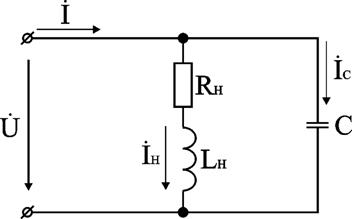
Рис. 2.24

Расчет емкости дополнительного конденсатора для обеспечения заданного cos φ проводится следующим образом. Пусть известны параметры нагрузки P_н, U и I_н . Можно определить cos_н

сos_н = P/(UI_н).

Из п. 2.8.3 следует, что подключение емкости не изменяет активную составляющую нагрузки

I_на = I_н cos_н = P_н/U (2.52)

Реактивная составляющая нагрузки I_нр может быть выражена через tg _н

I_нр = I_на tg _н.

При подключении емкости величина I_нр уменьшается на величину I_C.

Если задано, что коэффициент мощности в питающей линии должен быть равен cos , то можно определить величину реактивной составляющей тока в линии

I_р = I_а tg .

Уменьшение реактивной составляющей нагрузки с I_нр до I_р определяет величину тока компенсирующей емкости

I_C = I_нр - I_р = I_а (tg _н - tg ). (2.53)

Подставляя в уравнение (2.53), значение I_на из (2.52) и учитывая, что I_C = U / X_C = U ωC, получим U ωC = P_н / U · (tg φ_н - tg φ), откуда для емкости конденсатора имеем

C = P_н / ωU² · (tg _н - tg ).

Для больших значений P_н величина емкости C может оказаться слишком большой, что технически трудно реализовать. В этом случае используют синхронные компенсирующие машины.

2.10. Комплексный (символический) метод расчета цепей синусоидального тока

Все параметры цепи представляются в комплексной форме.

 – комплексное мгновенное значение;  – комплексное действующее значение силы тока;  – комплексное действующее значение напряжения.

Пример.

Законы Ома и Кирхгофа в комплексной форме

Достоинство комплексного метода: при его применении в анализе цепей переменного тока можно применять все известные методы анализа постоянного тока.

Закон Ома

Под законом Ома в комплексной форме понимают:

Í = Ú / Z

Комплексное сопротивление участка цепи представляет собой комплексное число, вещественная часть которого соответствует величине активного сопротивления, а коэффициент при мнимой части – реактивному сопротивлению.

По виду записи комплексного сопротивления можно судить о характере участка цепи:

R + j X — активно-индуктивное сопротивление;

R – j X — активно-емкостное.

Примеры.

Первый закон Кирхгофа в комплексной форме

Алгебраическая сумма комплексных действующих значений токов в узле равна нулю.

Второй закон Кирхгофа в комплексной форме

В замкнутом контуре электрической цепи алгебраическая сумма комплексных действующих значений ЭДС равна алгебраической сумме комплексных падений напряжений в нём.

.

При использовании символического метода можно пользоваться понятиями мощностей. Но в комплексной форме можно записать только полную мощность:

где Ï — комплексно-сопряженный ток

S cos  ± j Ssin  = P ± jQ.

Полная мощность в комплексной форме представляет собой комплексное число, вещественная часть которого соответствует активной мощности рассматриваемого участка, а коэффициент при мнимой части – реактивной мощности участка. Значение знака перед мнимой частью: “+” означает, что напряжение опережает ток, нагрузка – активно-индуктивная; “–” означает, что нагрузка - активно-емкостная.