2.6. Мощности в цепях переменного тока

По аналогии с мощностью в цепях постоянного тока P = U I, в цепях переменного тока рассматривают мгновенную мощность p = u i. Для упрощения рассмотрим мгновенную мощность в каждом из элементов R, L и С отдельно.

1. Элемент r (резистор)

Зададим напряжение и ток в виде соотношений

u(t) = U_m sin(ωt + ψ_u),

i(t) = I_m sin(ωt + ψ_i).

Известно, что для резистора ψ_u = ψ_i, тогда для р получим

p(t) = u(t) i(t) = U_m I_m sin²(ωt + ψ_i). (2.32)

Из уравнения (2.32) видно, что мгновенная мощность всегда больше нуля и изменяется во времени. В таких случаях принять рассматривать среднюю за период Т мощность

. (2.33)

Если записать U_m и I_m через действующие значения U и I: 

,  ,

то получим

P = U I. (2.34)

По форме уравнение (2.34) совпадает с мощностью на постоянном токе. Величину Р равную произведению действующих значений тока и напряжения называют действующей мощностью. Единицей ее измерения является Ватт (Вт).

2. Элемент l (индуктивность)

Известно, что в индуктивности соотношение фаз ψ_u = ψ_i + 90°. Для мгновенной мощности имеет

. (2.35)

Усредняя уравнение (2.35) по времени за период Т получим

.

Для количественной оценки мощности в индуктивности используют величину Q_L равную максимальному значению р_L

Q_L = (U_m I_m)/2 (2.36)

и называют ее реактивной (индуктивной) мощностью. Единицей ее измерения выбрали ВАр (вольт-ампер реактивный). Уравнение (2.36) можно записать через действующие значения U и I и используя формулу U_L = I X_L получим

Q_L = I² X_L. (2.37)

3. Элемент с (ёмкость)

Известно, что в емкости соотношение фаз ψ_u = ψ_i - 90°. Для мгновенной мощности получаем

p_C(t) = u(t) I(t) = (U_m I_m) / 2 · sin(2ωt).

Среднее значение за период здесь также равно нулю. По аналогии с уравнением (2.36) вводят величину Q_C = I² X_C, которую называют реактивной (емкостной) мощностью. Единицей ее измерения также является ВАр.

Если в цепи присутствуют элементы R, L иС, то активная и реактивная мощности определяются уравнениями

P = U Icos, (2.37)

Q = Q_L - Q_C, (2.38)

Q = UIsin, (2.39)

где – угол сдвига фаз.

Вводят понятие полной мощности цепи

. (2.40)

С учетом уравнений (2.37) и (2.39), (2.40) можно записать в виде

S = U I. (2.41)

Единицей измерения полной мощности является ВА – вольт-ампер.

2.7. Цепь с последовательным соединением элементов

Проведем анализ работы электрической цепи с последовательным соединением элементов R, L, С.

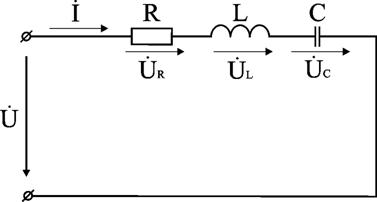
Положим, что в этой задаче заданы величины R, L, С, частота f, напряжение U. Требуется определить ток в цепи и напряжение на элементах цепи. Из свойства последовательного соединения следует, что ток во всех элементах цепи одинаковый. Задача разбивается на ряд этапов.

1. Определение сопротивлений.

Реактивные сопротивления элементов L и С находим по формулам

X_L = ωL, X_C = 1 / ωC, ω = 2πf.

Полное сопротивление цепи равно

,

угол сдвига фаз равен

 = arctg((X_L ̶ X_C) / R), (2.42)

2. Нахождение тока. Ток в цепи находится по закону Ома

I = U / Z, ψ_i = ψ_u + .

Фазы тока и напряжения отличаются на угол φ.

3. Расчет напряжений на элементах. Напряжения на элементах определяются по формулам

U_R = I R, ψ_uR = ψ_i ;

U_L = I X_L, ψ_uL = ψ_i + 90° ;

U_C = I X_C, ψ_uC = ψ_i - 90°.

Для напряжений выполняется второй закон Кирхгофа в векторной форме.

Ú = Ú_R + Ú_L + Ú_C.

4. Анализ расчетных данных. В зависимости от величин L и С в формуле (2.42) возможны следующие варианты:

X_L > X_C; X_L < X_C; X_L = X_C.

Для варианта X_L > X_C угол φ > 0, U_L > U_C. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид (рис. 2.16).

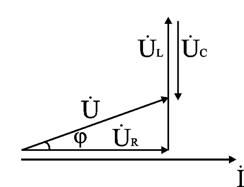
Рис. 2.16

Для варианта X_L < X_C угол φ < 0, U_L < U_C. Ток опережает напряжение на угол . Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид (рис. 2.17).

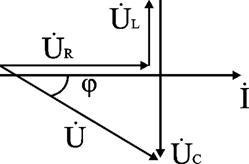
Рис. 2.17

Для варианта X_L = X_C угол  = 0, U_L = U_C. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление z=R наименьшее из всех возможных значений X_L и X_C. Векторная диаграмма напряжений имеет вид (рис. 2.18).

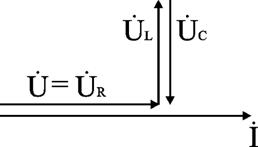
Рис. 2.18

Этот режим называется резонанс напряжений (U_L = U_C). Напряжения на элементах U_L и U_C могут значительно превышать входное напряжение.

Пример.

U = 220 B, f = 50 Гц, R = 22 Ом, L =  350 мГн, С =  28,9 мкФ.

X_L = ωL = 2πf L = 2 3,14 50 0,35 = 110 Ом;

X_C = 1 / ωC = 1 / (2πf C) = 110 Ом;

Z = R = 22 Ом,=0, I = U / R = 220 / 22 = 10 А, ψ_u = ψ_i;

U_L = U_C = I X_L = 10 · 110 = 1100 В.

В приведенном примере U_L и U_С превышают входное напряжение в 5 раз.