Сума, яку одержить власник боргового зобов`язання:

P=S-D=S (1-d ,

- кількість днів, що залишилась до кінця терміну облікування.

Задача 2

Тратта (перевідний вексель) виданий на суму 100 000 грн. з виплатою 17 листопада. Власник документу облікував його в банку 23 вересня (достроково) по обліковій ставці 8 %. Яку суму отримав власник при обліку векселя в банку?

n =7+31+17 =55 днів – кількість днів, що залишилась до кінця терміну облікування

P=S (1 –d n) =100000 (1 - 0, 08 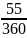) =98778,4 грн.

Визначення терміну позики і величини % ставки.

При розробці умов контракту та їх аналізі виникає необхідність у вирішенні вторинних задач, зокрема, визначенні терміну позики і розміру % ставки.

1.) Термін позики

А) в роках:

- для математичного обліку ;

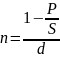- для банківського обліку.

Б) в днях:

, t - кількість днів, k - часова база

t= - для математичного обліку

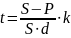- для банківського обліку

2.) Величина процентної ставки

i = - математичний облік

- банківський облік

Задача 3

Яким повинен бути термін позики в днях , щоб борг в 1млн. грн. виріс до 1,2 млн. грн. при умові , що нараховуютьсяі прості % за ставкою 25% річних. (К=365 днів).

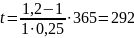дні.

Задача 4

В контракті передбачається погашення боргу в 110 млн. грн. через 120 днів. Першопочаткова сума боргу – 90 млн. грн. Визначити дохідність кредитної операції для кредитора у вигляді річної ставки процента та облікової ставки(К=360 дн.)

%.

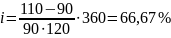
2. Дисконтування за складними фінансовими ставками Математичне дисконтування

P=

Нарощення і дисконтування за складною обліковою ставкою (банківський облік)

S=P , P=S

Банківське дисконтування може проводитись m раз в році, тоді застосовують номінальну облікову ставку f, в кожному періоді дисконтування здійснюється за за ставкою f/m, а дисконтування проводять за формулою:

P= S (1-

Задача 5

Яка сума дисконту при продажу фінансового інструменту на 5 тис. грн., якщо термін до його погашення 2,5 роки, а покупець застосував складну річну облікову ставку 8%. Порахувати те ж при умові, що дисконтування проводиться 4 рази в році.

P=5000 грн.

D=5000-4059,19=940,81 грн.

Дисконтування проводиться 4 рази в році (m=4)

P=5000(1-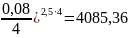 грн.

D=5000-4085, 36=914, 64 грн.

Фінансові ренти (ануїтети).

У більшості комерційних, банківських і фінансових операціях передбачаються не окремі разові платежі, а деяка їх послідовність протягом певного періоду часу (наприклад, доходи і витрати підприємства, погашення заборгованостей, сплата податків, страхові внески, внески для створення цільових фондів тощо).

Потік платежів, всі члени якого однонаправлені (або лише надходження, або лише виплати), а часові інтервали однакові, називають фінансовою рентою (рентою) або ануїтетом (з англ. annuity). Це серія рівновеликих платежів (внесків) протягом визначеної кількості періодів.

Рента характеризується такими параметрами:

член ренти – це розмір окремого платежу;

період ренти -часовий інтервал між двома послідовними платежами;

строк ренти - час від початку першого періоду ренти до кінця останнього періоду.

За моментом здійснення платежів в межах періоду ренти розрізняють:

1.) звичайні ренти (постнумерандо), якщо платежі здійснюються в кінці відповідного періоду;

2.) вексельні ренти (пренумерандо), якщо платежі здійснюються на початку відповідного періоду (перший платіж здійснюється на момент початку відліку часу).

У більшості випадків аналіз потоку платежів передбачає розрахунок однієї з двох узагальнюючих характеристик:

нарощеної суми ()– сума всіх членів потоку платежів з нарахованими на них до кінця строку ренти процентами;

теперішньої вартості – сума всіх його членів, дисконтавана на початок строку ренти (на о-ий рік) або якийсь інший випереджуючий час (цю величину ще називають зведеною або капіталізованою ціною ренти).

Теперішня вартість показує, яку суму слід було б мати початково, щоб, розбивши її на рівні внески, на які нараховані встановлені % протягом терміну ренти, можна було б забезпечити отримання нарощеної суми.

0

Кінець 1 року І початок 2 року

Кінець 2 року

Кінець 3 року

Кінець 4 року

Кінець 5 року

Кінець 6 року

Вісь часу

платіж

платіж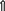

платіж

платіж

платіж

платіж

Рис. 1. Схема звичайного ануїтету (постнумерандо)

0

Кінець 1 року І початок 2 року

Кінець 2 року

Кінець 3 року

Кінець 4 року

Кінець 5 року

Кінець 6 року

Вісь часу

платіж платіж

платіж

платіж

платіж

платіж

Рис. 2. Схема авансового ануїтету (пренумерандо)