Дисконтування за простими і складними ставками.
Дисконтування є фінансово-математичною моделлю визначення поточної (теперішньої) вартості грошових потоків, надходження яких, як очікується, матиме місце у майбутньому протягом певного планового періоду. Теперішня вартість майбутніх грошових потоків визначається шляхом приведення – дисконтування на величину процента, який міг би бути заробленим у випадку, коли б грошові кошти були доступні для їх використання на момент оцінювання. Необхідність дисконтування, зокрема, виникає при покупці банком чи іншими фінансовими установами короткострокових платежів, зобов`язань (векселі, тратти), розрахунок по яких проводиться в майбутньому.
Дисконтування за простими фінансовими ставками
У фінансовій практиці часто стикаються з ситуацією, що обернена нарощенню: за даною сумою S, яку необхідно сплатити за час n, необхідно визначити початкову величину Р.
Розраховувати Р за значенням S необхідний тоді, коли % з суми стягуються наперед безпосередньо при видачі позики. В цих випадках говорять,що сума S дисконтується, а сам процес нарахування % та їх стягнення називається обліком або дисконтуванням. Утримані % називають дисконтом. Величину Р, знайдену за допомогою дисконту, називають теперішньою величиною суми S або теперішньою (капіталізованою, поточною) вартістю.
В залежності від цілей дисконтування і видів % ставок використовують 2 методи дисконтування:
1)математичний (використовується ставка нарощення i);
2)банківський (комерційний) облік (використовується облікова ставка d).
Математичне дисконтування – визначення теперішньої величини нарощеної суми. Задача в цьому випадку формулюється так:
яку початкову суму необхідно надати в борг, щоб отримати в кінці строку суму S за умови, що на борг нараховуються % і.
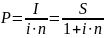
І – проценти за весь час позики;
-
дисконтний множник, що показує, яку
частку складає величина боргу в кінцевій
його сумі;
n – термін позики (або кількість інтервалів у плановому періоді).
Задача 1
Через 180 днів після підписання договору боржник заплатить 310 тис. грн. Кредит надано під 16% річних (простих). Якою була сума боргу, якщо часова база 365 днів, і яку суму дисконту сплачено боржником?
P=
грн., D
= S-P
= 310000-287328=22672 грн.
Банківський облік (дисконтування за обліковою ставкою)– це процес нарахування і утримання відсотків наперед. Це визначення початкової або теперішньої суми боргу Р, коли відома кінцева сума S ,термін користування грошима n, облікова ставка d.
Механізм банківського обліку такий: банк чи інша фінансова установа до настання строку платежу за борговим зобов`язанням купує його у власника за ціною меншою від суми, вказаної на борговому зобов`язанні, тобто обліковує його з дисконтом (знижкою). Одержавши при настанні строку платежу гроші, банк реалізує (отримує) дисконт.
Розмір дисконту, який реалізується (отримується) банком:
D=S
,.
n=t/k , t – кількість днів, k – часова база.
При простій обліковій ставці береться точне число днів t, а часова база k, як правило, 360 днів.