
- •Нарощення (компаундування) за простими і складними процентами
- •1.Нарощена сума при простій постійній ставці.
- •2.Нарощена сума при складній ставці.
- •Дисконтування за простими і складними ставками.
- •Дисконтування за простими фінансовими ставками
- •Розмір дисконту, який реалізується (отримується) банком:
- •Сума, яку одержить власник боргового зобов`язання:
- •1.) Термін позики
- •2.) Величина процентної ставки
- •Дисконтування за складними фінансовими ставками Математичне дисконтування
- •Нарощення і дисконтування за складною обліковою ставкою (банківський облік)
- •Фінансові ренти (ануїтети).
- •Нарощена сума звичайної ренти (ануїтету постнумерандо).
- •Нарощена сума звичайної (постнумерандо) ренти
- •Теперішня вартість звичайної (постнумерандо) ренти
- •Нарощена сума і теперішня вартість вексельної (пренумерандо) ренти
- •Оцінка інфляції
- •Формування фінансової структури капіталу та оцінка його вартості
- •Управління інвестиціями Управління фінансовими інвестиціями Оцінка вартості окремих фінансових інструментів інвестування (фінансових активів)
Методичний інструментарій оцінювання вартості грошей у часі.
Визначення кількісної оцінки зміни вартості грошей у часі є основою більшості фінансових розрахунків та математико-статистичних моделей, які використовуються у фінансовому менеджменті. Оцінка вартості грошей у часі використовується при управління сукупністю фінансових процесів, які виникають у період функціонування суб`єкта господарювання – управлінні інвестиціями, грошовими розрахунками, дебіторською і кредиторською заборгованістю, ціновою політикою підприємства та ін. Розміщуючи капітал в один з обраних проектів, фінансовий менеджер планує не тільки з часом повернути вкладені гроші, але й отримати бажаний економічний ефект.
Зміну вартості грошей зумовлює сукупність чинників, які визначають рівень їх корисності для власника у конкретний момент часу.
Основними причинами зміни вартості грошей в часі є:
інфляційні (або дефляційні) процеси в економіці (ризик зміни купівельної спроможності грошей). Інфляція пов`язана із загальним підвищенням цін в країні: коли зростають ціни, зменшується вартість грошової одиниці. Отже купівельна спроможність грошової одиниці сьогодні вища, ніж буде завтра. У випадку дефляційних процесів, навпаки, купівельна спроможність (корисність) грошових коштів у наступному періоді зростає, що позитивно впливає на їх вартість у часі, і, як наслідок, розпоряджатися тією ж самою сумою грошей вигідніше не у поточному періоді, а в наступному.
комерційна надійність (ненадійність) комерційних партнерів (наявність ризику невиконання зобов'язань). Через невпевненість у надійностфі партнерів ризик з часом зростає. Більшість підприємців хоче уникнути ризику, тому вище цінує гроші, які є сьогодні, ніж ті, що мають бути в майбутньому. Ті суб`єкти підприємницької діяльності, які погоджуються віддавати наявні гроші сьогодні в обмін на їх більшу кількість у майбутньому, очікують вищої компенсації у вигляді певної винагороди за цей ризик.
віддання переваги підприємцями наявним грошам. Підприємці надають перевагу наявним грощам перед очікуваними у майбутньому, тобто «цінують» високу ліквідність, втіленням якої і є наявні гроші. При інвестування підприємець міняє «живі» гроші на ризикованіші доходи у майбутньому. Такий обмін можливий, коли майбутні доходи будуть достатньо високими. Це є «виправданням» ризику інвестора, оскільки він сподівається на високу винагороду як компенсацію за втрату ліквідності.
Часова вартість грошей як результат викладених вище чинників може розглядатися з позицій:
теперішньої вартості майбутніх грошових потоків;
майбутньої вартості грошей, які є у розпорядженні на поточний момент часу.
Основним об`єктом кількісної оцінки вартості грошей у часі є грошові потоки як результат проведення фінансових операцій або реалізації фінансових відносин. Проте, положення концепції часової вартості грошей, її принципи та математичні моделі можуть використовуватися при визначенні вартості активів, відмінних від грошових коштів, зокрема, інструментів фінансового ринку (цінних паперів, деривативів).
Зв`язок між вартістю грошей у теперішній і майбутній час можна зобразити схематично (рис.1).
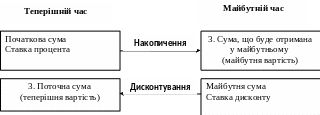
Рис.1. Структурно-логічна схема зв`язку між вартістю грошей
у теперішній і мабутній час.
Процес за якого гроші рухаються від поточного часу до майбутнього (за заданої початкової суми та ставки процента) є накопиченням (компаундуванням, compounding). Процес за якого гроші рухаються від майбутнього до теперішнього часу (за заданої майбутньої суми і дисконтної ставки), називається дисконтуванням (discounting).
Різноманітність завданнь щодо визначення зміни вартості грошей у часі можна звести у такі групи:
накопичення (компаундування, compounding) – визначення майбутньої вартості грошей (FV, future value). Компаундування передбачає отримання адекватної величини вартості наявних грошових ресурсів, зіставленої з фінансовими показниками для проведення фінансового планування операцій (діяльності) майбутніх періодів.
дисконтування (discounting) – визначення поточної (теперішньої) вартості грошей (PV, present value). Спрямоване на отримання адекватної величини вартості майбутніх грошових потоків, зіставленої з фінансовими показниками для проведення аналізу употочному періоді.
Завдання щодо визначення вартості грошей
Компаундування Дисконтування
Просте Ануїтетів (ренти) Просте Ануїтетів (ренти)
звичайної авансової звичайної авансової
Під простим нарощенням розуміють майбутню вартість грошей вкладену одноразово на певний термін під певний процент. Рента – це серія рівновеликих платежів.
Нарощення (компаундування) за простими і складними процентами
1.Нарощена сума при простій постійній ставці.
S=P
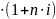 ,
,
де і- ставка %;
S (FV)- нарощена сума на кінець терміну позики;
P (PV) – початкова сума позики;
n – тривалість позики в роках;
n=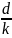 – k-тривалість
року в днях, d-кількість
днів позики.
– k-тривалість
року в днях, d-кількість
днів позики.
I=P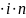 - проценти за весь час позики.
- проценти за весь час позики.
S=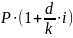
Якщо k=365 (366) днів, то визначаємо точні проценти (день видачі і день погашення вважається за 1 день), якщо k=360 днів – звичайні або комерційні проценти (приймається, що тривалість будь-якого місяця 30 днів).
Якщо d визначається точно, то обраховується фактичне число днів позики. Якщо d визначається приблизно,то приймають його d= 30днів і це є наближене число днів позики.
Застосовують такі прості процентні ставки:
точні проценти з фактичним числом днів позики з фактичним числом днів позики (k=365 (366) днів; за півріччя термін позики 182 дні). Цей варіант дає найточніші результати, його застосовують центральні банки багатьох країн, а в деяких країнах (Англія) і комерційні банки. Позначають 365/365 або act/act і ще наз. англійськими.
звичайні % з точним числом днів позики (ще їх називають банківськими або французькими). Цей метод поширений в позичкових операціях комерційних банків (напр., Франції). 3Позначають 365/360 або act/360.
звичайні % з наближеним числом днів позики. Застосовуються тоді, коли не вимагається великої точності (КБ уНімеччині). Познач. 360/360.
Задача 1
Визначити % і нарощену суму боргу, якщо початкова сума боргу 700 тис.грн., термін позики 4 роки, % - прості,ставка боргу 20%
І=700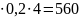 грн.
грн.
S=700+560=1260 грн.
Задача 2
Позика в розмірі 100 тис. грн. видана 20 січня до 5 жовтня включно під 8% річних, рік невисокосний. Знайти розмір погашувального платежу (нарощену суму) за трьома варіантами простих процентів..
а) d=11+28+31+30+31+30+31+30+5=258дн. – точне число днів позики
б)
d=10+30 дн.-наближене
число
днів позики
дн.-наближене
число
днів позики
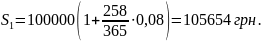 -
точні % з фактичним числом днів позики;
-
точні % з фактичним числом днів позики;
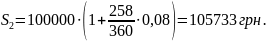 -
звичайні % з фактичним числом днів
позики;
-
звичайні % з фактичним числом днів
позики;
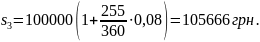 -
звичайні
% з наближеним числом днів позики.
-
звичайні
% з наближеним числом днів позики.
Вкладати гроші найвигідніше під звичайні % з фактичним (точним) числом днів позики, а брати кредити – під точні % з фактичним числом днів позики.
Інколи в кредитних умовах передбачаються змінні в часі процентні ставки, тоді нарощена сума на кінець періоду визначається формулою:
S=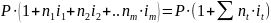 ,
де
,
де
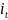 -
ставка простих процентів в періоді t;
-
ставка простих процентів в періоді t;
t = 1,2,…,m;
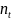 -
тривалість періоду; n=
-
тривалість періоду; n=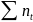
Задача 3
Контракт передбачає такий порядок нарахувань: перший рік 16%, а в кожному наступному півріччі ставки процента підвищується на 0,5%. Визначити множник нарощення і нарощену суму за 2,5 роки при величині вкладу 100 тис.грн.
1+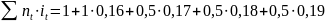 =1,43
=1,43
S=100000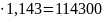 грн.
грн.
2.Нарощена сума при складній ставці.
В середньо- і довгострокових фінансово-кредитних операціях, якщо % не виплачуються зразу після їх нарахування, а приєднуються до суми боргу, то для визначення нарощеної суми застосовують складні відсотки.
База для нарахування змінюється (збільшується) з кожним кроком в часі. Приєднання нарахованих % до суми, що послужила базовою, називають капіталізацією відсотків.
При складній ставці % нарощена сума розраховується так:
FV=S=P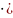
Коли n не є ціле число,множник нарощення має вигляд
А)
простий метод

Б)
змішаний метод
(1+i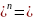 ,
де
,
де
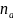 -
ціле число років;
-
ціле число років;
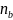 - дробова частина року.
- дробова частина року.
Задача 1
Яким стане борг в 10 тис. грн. через 5 років при рості за складною ставкою 5,5% річних.
S=10 000 грн.
Задача 2
Кредит в розмірі 30000 грн. виданий на 3 роки і 160 днів. Якою буде сума боргу на кінець періоду, якщо передбачена в контракті ставка складних відсотків рівна 6,5% річних і передбачений змішаний метод нарахування % :
S=30000 37271 грн.
Якщо по умовах контракту передбачається зміна рівня % ставки в часі,то для нарахування процентів застосовують таку формулу для обчислення нарощеної суми:
1)перемінна ставка
S= P , де
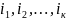 -
значення ставок процентів в часі;
-
значення ставок процентів в часі;
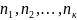 – періоди,
протягом яких застосовуються відповідні
ставки.
– періоди,
протягом яких застосовуються відповідні
ставки.
Задача 3
Ставка по позиці встановлена на рівні 8,5% річних + маржа 0,5% перші 2 роки і 0.75% наступних 3 роки. Визначити множник нарощення.
.
Нарахування складних % m раз в році
Якщо
нарахування % здійснюється не 1 раз, а m
раз в році, то в цьому випадку в контракті
обговорюється
номінальна
ставка процентів
(j),
виходячи
з якої
визначається величина
ставки,
яка
застосовується
в кожному періоді
нарахування
. Якщо % нараховані m
раз в році,
то
в кожному періоді застосовується
ставка
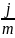 .
.
S=P ,
N – кількість періодів нарахування.
Якщо j=12% і відбувається поквартальне нарахування% протягом 5 років, то
=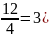 ;
N=n
;
N=n
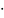 m=5
років
4 квартали
=
20
періодів нарахувань.
m=5
років
4 квартали
=
20
періодів нарахувань.
Задача 4
Початкова сума позики 10 тис. грн., термін 5 років, проценти нараховуються в кінці кожного кварталу, номінальна річна ставка 5%. Визначити нарощену суму позики.
N=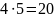 періодів; S=
10000
періодів; S=
10000 =12820
грн.
=12820
грн.
