2.4 Решение линейных неоднородных уравнений порядка n
Прежде чем учиться решать уравнения с постоянными коэффициентами, познакомимся с некоторыми теоретическими проблемами для более общего случая, то есть для уравнений с переменными коэффициентами
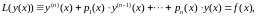(2.11)
где
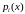и
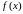– функции, непрерывные на
;
– дифференциальный оператор.
Пусть
дана некоторая функция
,
являющаяся частным решением (2.11). Если
- решение, то
.
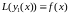Возьмём функцию и выясним, при каких условиях может быть решением (2.11).
Подставим в это уравнение:
.
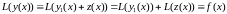Так
как
,
то последнее равенство выполняется при
условии, что
.
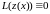Это возможно, если общее решение соответствующего однородного уравнения, полученного из (2.11) заменой на нуль.
Тогда
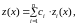
где:
–
константы;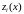
–
ФСР соответствующего однородного
уравнения.
Отсюда
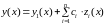
есть общее решение уравнения (2.11), состоящее из частного решения (2.11) и общего решения соответствующего однородного уравнения.
Пусть правая часть задана суперпозицией функций
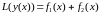
Тогда, если и – частные решения и при этом
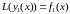и
,
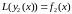то
– частное решение исходного уравнения.
Теперь познакомимся с методами построения общего решения неоднородных уравнений.
2.5 Метод вариации произвольных постоянных(метод Лагранжа)
Будем считать, что для соответствующего однородного уравнения из (2.11) известна ФСР . Заметим, что для частного случая, когда – константы, её легко построить.
Запишем
общее решение соответствующего
однородного уравнения, но
у нас будут не константы, а некоторые
непрерывные и дифференцируемые функции
,
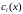причём такие, что полученное решение
удовлетворяет заданному неоднородному
уравнению (2.11):
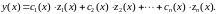(2.12)
Для
нахождения
продифференцируем
раз, причём подчиним
дополнительным (произвольным)
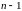условиям. Вычисляя
,
,…,
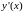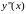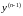от
(2.12), сгруппируем члены содержащие
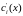и приравняем эти выражения к нулю:
(2.13)
Для
производной
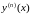в (2.13) не применяется дополнительное
условие равенства нулю части выражения,
содержащее
.
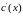Подставим
,
,…,
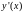в уравнение (2.11). Для этого (2.13) умножим
на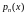
,
,…,
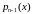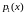,1
соответственно и сложим.
Тогда получим
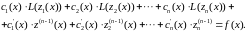
Так
как
– ФСР, то
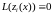и
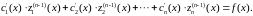(2.14)
Используя (n-1) произвольных условий из (2.13) и (2.14), запишем систему уравнений для нахождения :
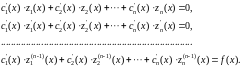(2.15)
Если
в (2.15) представим
как компоненты вектора
,
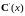то определитель матрицы, составленный
из
и (n-1) их производных – вронскиан и не
равен нулю. То есть (2.15) имеет единственное
решение, которым (как известно из линейной
алгебры) будет
,
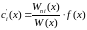где:
–
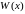вронскиан;
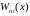– алгебраическое дополнение n-ой строки
и
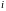столбца;
–
правая часть (2.11).
Тогда
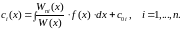
Подставим вычисленные в (2.12) и получим общее решение уравнения (2.11):
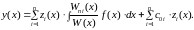(2.16)
В (2.16) первое слагаемое – частное решение неоднородного уравнения, а второе – общее решение соответствующего однородного уравнения.
Для
уравнения с постоянными коэффициентами
(
–
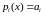константы)
легко найти, и используя полученные
выражения (2.15) и (2.16), построить общее
решение неоднородного уравнения.
Пример. Построим общее решение не однородного ДУ
.
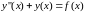Соответствующим однородным уравнением и его ФСР будут:
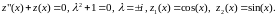
Запишем систему уравнений для нахождения по (2.15):
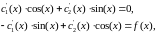
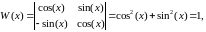
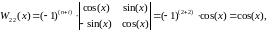
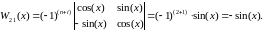
Тогда:
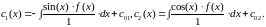
И общее решение будет
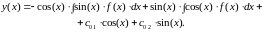
Для разных правых частей (разных ) будем получать разные частные решения неоднородного уравнения. При этом общее решение соответствующего однородного уравнения будет неизменным.