
- •Предисловие
- •Глава 2 содержит материалы по изучению методов аналитического решения линейных уравнений порядка n как однородных так и не однородных, построение их общего решения и задачи Коши.
- •Глава 1 дифференциальные уравнения первого порядка
- •1.1 Основные понятия и определения
- •1.2 Геометрическое истолкование решений Поле направлений. Интегральные кривые. Задача Коши
- •1.3 Уравнений с разделяющимися переменными
- •Особые решения
- •1.4 Линейные неоднородные уравнения
- •Свойства решений однородного линейного уравнения
- •1.5 Уравнения в полных дифференциалах
- •Признак уравнения в полных дифференциалах Построение общего интеграла.
- •Задача Коши.
- •Интегрирующий множитель
- •Краткий итог рассмотренных уравнений
- •1.6 Уравнение Бернулли
- •1.7 Теорема существования и единственности решения задачи Коши
- •Особые решения
- •Глава 2 дифференциальные уравнения порядка n
- •2.1 Основные понятия и определения
- •2.2 Фундаментальная система решений. Общее решение однородного лду. Задача Коши
- •2.3 Решение однородных лду порядка n с постоянными коэффициентами
- •2.4 Решение линейных неоднородных уравнений порядка n
- •2.5 Метод вариации произвольных постоянных(метод Лагранжа)
- •2.6 Метод неопределённых коэффициентов
- •2.7 Метод Коши
- •Контрольные вопросы
- •Глава 3 системы дифференциальные уравнения порядка n
- •3.1 Основные понятия и определения
- •Некоторые свойства решений однородной системы
- •3.2 Решение не однородной системы
- •3.3 Однородные системы уравнений с постоянной матрицей
- •3.4 Матричный метод решения сду
- •Характеристические числа действительные, разные
- •Характеристические числа комплексные
- •3.5 Автономные системы и их фазовые портреты
- •Глава 4 не линейные системы дифференциальных уравнений
- •4.1 Исследование качественной структуры
- •Фазового пространства в окрестности особых точек
- •4.2 Возможный характер простых состояний равновесия
- •1. . Корни действительные и одинаковых знаков: ;
- •Направления, в которых траектории стремятся к простым состояниям равновесия
- •Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия
- •4.3 Нелинейные консервативные системы
- •4.4 Уравнение Вольтера
- •4.5 Уравнения Гамильтона
- •Теорема Лиувиля
- •4.6 Предельные циклы и автоколебания
- •4.7 Уравнение Ван – Дер – Поля
- •4.8 Приближённый метод исследования предельных циклов
- •4.9 Некоторые признаки существования и отсутствия предельных циклов
- •Критерий Бендиксона отсутствия предельных циклов
- •4.10 Использование точечных отображений для изучения фазовых портретов
- •Список литературы
2.2 Фундаментальная система решений. Общее решение однородного лду. Задача Коши
Определение «фундаментальная система решений» является основополагающим при построении решения ЛДУ порядка n. Легко заметить, что это понятие базируется на вышеизложенных определениях и критериях о линейной зависимости (или независимости) функций.
Совокупность решений ЛДУ, определённых и линейно независимых в интервале , называется фундаментальной системой решений (ФСР) в этом интервале. Для того чтобы система из решений была фундаментальной, необходимо и достаточно, чтобы вронскиан этих решений был отличен от нуля хотя бы в одной точке интервала непрерывности коэффициентов уравнения (2.2), т.к. если вронскиан отличен от нуля хотя бы в одной точке интервала , то он отличен от нуля на всём интервале. Все решения ненулевые.
Теперь, используя третье свойство решений ЛДУ, мы можем записать общее решение однородного дифференциального уравнения.
Если – фундаментальная система решений уравнения , то
 (2.4)
(2.4)
есть
общее решение
однородного
ЛДУ порядка
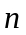 в области:
в области:
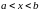 ,
,
 ,
,
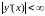 ,…
,…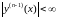 ,
,
( – произвольные постоянные числа).
– произвольные постоянные числа).
Продифференцируем
(2.4)
 раз:
раз:
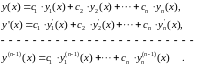 (2.5)
(2.5)
Если
мы зададим числовые значения
, ,
…,
,
…,
 ,
то сможем разрешить линейную систему
уравнений (2.5) по отношению к
,
причём единственным образом, так как
определитель этой системы (вронскиан)
не равен нулю. В выражении (2.4) содержатся
все решения уравнения
.
,
то сможем разрешить линейную систему
уравнений (2.5) по отношению к
,
причём единственным образом, так как
определитель этой системы (вронскиан)
не равен нулю. В выражении (2.4) содержатся
все решения уравнения
.
Подставив
найденные коэффициенты в (2.4), получим
решение задачи Коши для однородного
уравнения порядка
с начальными условиями
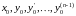 .
.
2.3 Решение однородных лду порядка n с постоянными коэффициентами
Однородные ЛДУ порядка с постоянными коэффициентами записываются следующим образом:
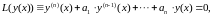 (2.6)
(2.6)
где
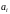 – вещественные константы.
– вещественные константы.
Задача построения общего решения (2.6) будет решена, если будет найдена фундаментальная система решений.
1. Случай действительных различных корней характеристического уравнения
Для уравнения первого порядка
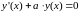 ,
,
решение запишется в виде
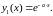
Эйлер
предложил и решение уравнения (2.6) искать
в таком же виде, т.е.
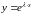 .
Если данная функция
решение (2.6), то она должна обращать это
уравнение в тождество:
.
Если данная функция
решение (2.6), то она должна обращать это
уравнение в тождество:

где
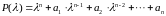
–
характеристический
полином, который легко получить из
однородного ЛДУ, заменив производные
от
на
в соответствующей степени. При коэффициенте
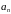 0=1.
Ясно, что
0=1.
Ясно, что
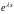
решение для тех ,
которые обращают
решение для тех ,
которые обращают
 в нуль.
в нуль.
Тогда
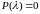 – характеристическое уравнение. Его
корни
– характеристическое уравнение. Его
корни
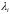 – характеристические числа однородного
уравнения.
– характеристические числа однородного
уравнения.
Пусть
все
- различные и вещественные числа.
Подставив
в функцию
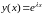 ,
найдём
вещественных частных решений (2.6):
,
найдём
вещественных частных решений (2.6):

Эти решения линейно независимые (их вронскиан не равен нулю для всех ), т.е. составляют фундаментальную систему решений (ФСР).
Тогда согласно (2.4)

есть общее решение линейного однородного уравнения порядка с постоянными коэффициентами (2.6), где:
– характеристические числа;
– произвольные коэффициенты;
– порядок уравнения (порядок старшей производной);
 – фундаментальная
система решений.
– фундаментальная
система решений.
Задача Коши для заданных числовых значений приводит к решению системы алгебраических уравнений (2.5) относительно .
Пример. Дано дифференциальное уравнение
 .
.
Характеристический полином запишется в виде
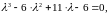
а
характеристические числа (корни данного
полинома) будут
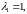
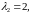

Тогда
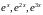 ФСР,
а общим решением будет функция
ФСР,
а общим решением будет функция
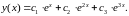
Решим задачу Коши для начальных условий:
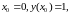


Запишем по (2.5) систему уравнений для заданных начальных условий:

После подстановки численных значений начальных условий получим систему алгебраических уравнений по отношению :
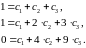
Решив
последнюю систему, получим:
 =0.5,
=0.5,
 =1,
=1,
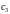 =
-0.5, и решение в форме Коши будет иметь
вид
=
-0.5, и решение в форме Коши будет иметь
вид

2. Случай различных комплексных корней характеристического уравнения
Пусть среди корней характеристического полинома есть некоторый комплексный корень:
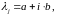
где
 и
–
числа,
.
и
–
числа,
.
Так как все коэффициенты полинома вещественные, тогда есть и сопряжённый ему корень
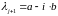 .
.
Таким
образом, решение для корня
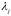 будет комплексным.
будет комплексным.
Ранее
было показано, что каждая комплексная
функция, являющаяся решением ЛДУ,
порождает два вещественных решения,
причём линейно независимых
 ,
т.е. входящих в фундаментальную систему
решений:
,
т.е. входящих в фундаментальную систему
решений:

Для сопряжённого корня решениями будут:
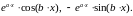
При этом первые решения совпадают, а вторые линейно зависимы. Таким образом, сопряжённый корень не порождает новых вещественных, линейно независимых решений, и соответствующие ему функции не включаются в ФСР.
Всего получим решений вида:

образующих фундаментальную систему решений, а общее решение запишется в следующей форме
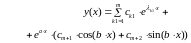 .
.
Если число комплексных корней больше двух, то в этом случае общее решение запишется в виде
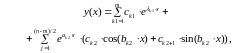 (2.7)
(2.7)
где
 – число корней действительных разных;
– число корней действительных разных;
– порядок дифференциального уравнения;
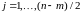 ;
;
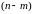 – число
комплексных и сопряжённых корней;
– число
комплексных и сопряжённых корней;
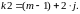
Пример. Построим общее решение уравнения
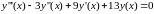 .
.
Найдем характеристическое уравнение и его корни:

Фундаментальной
системой решений, для данных
 ,
будут функции:
,
будут функции:

Тогда общим решением заданного однородного уравнения с постоянными коэффициентами будет функция
 .
.
3. Случай кратных корней.
Для
пояснения термина «кратные корни»
рассмотрим полином второго порядка
 .
.
Тогда:
 ,
,
 .
.
В
примере полином имеет два кратных корня.
В общем случае число кратных корней
может быть
 (
),
где
порядок дифференциального уравнения
(порядок полинома).
(
),
где
порядок дифференциального уравнения
(порядок полинома).
Теперь изучим, как наличие кратных корней связано с построением ФСР для уравнений с постоянными коэффициентами.
Пусть
1
–
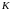 кратный
корень характеристического уравнения.
Тогда
кратный
корень характеристического уравнения.
Тогда
 (2.8)
(2.8)
То
есть производные от
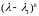 по
по
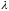 при
при
 до
до
 порядка равны нулю. Продифференцируем
раз по
тождество
порядка равны нулю. Продифференцируем
раз по
тождество
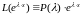
и получим
 (2.9)
(2.9)
Напомним, что дифференциальный оператор, определяющий конкретный вид уравнения.
В
(2.9)
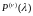 производная порядка
производная порядка
 от характеристического полинома по
переменной
от характеристического полинома по
переменной
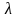 .
Тогда на основании (2.8):
.
Тогда на основании (2.8):
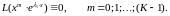 (2.10)
(2.10)
Отсюда
функции:
 являются решениями уравнения (2.6). Они
линейно независимы (их вронскиан не
равен нулю ни в одной точке интервала
по
)
и составляют фундаментальную систему
из K решений.
являются решениями уравнения (2.6). Они
линейно независимы (их вронскиан не
равен нулю ни в одной точке интервала
по
)
и составляют фундаментальную систему
из K решений.
Пример 1. Построим общее решение уравнения
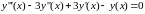 .
.
Характеристическое уравнение и его корни равны:
 ,
,
 ,
,
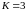 .
.
Тогда
ФСР запишется следующим образом:
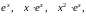
а
общее решение:
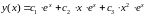 .
.
Пример 2. Построим общее решение уравнения
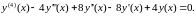
Запишем характеристическое уравнение и найдем его корни:
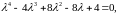
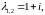

B
данном примере мы имеем корни комплексные
сопряжённые, кратные. Для построения
ФСР воспользуемся общими правилами, с
которыми уже знакомы: сопряжённые корни
( )
не порождают новых, линейно независимых
решений, а для
)
не порождают новых, линейно независимых
решений, а для
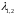
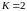 .
.
Тогда ФСР будет
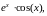
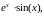


а общее решение

В заключение этого раздела укажем последовательность действий при решении однородных уравнений порядка с постоянными коэффициентами.
Записываем характеристический полином
 .
.Находим характеристических корней этого полинома.
Записываем ФСР согласно виду характеристических чисел (корни действительные разные; комплексные; кратные).
Записываем общее решение.
Решаем задачу Коши (если заданы начальные условия):
а) вычисляем (n-1) производных от общего решения;
б)
в полученную систему уравнений подставляем
численные значения:

в) решаем полученную систему алгебраических уравнений по отношению к произвольным коэффициентам ;
г) записываем общее решение в форме Коши с найденными числовыми значениями .
