Краткий итог рассмотренных уравнений

Рассмотренные уравнения в общем случае имеют вид . При этом:

1. для уравнения с разделёнными переменными:

;

2. для уравнения с разделяющимися переменными:

;

3. для линейного уравнения:

;

4. для уравнения в полных дифференциалах:

.

1.6 Уравнение Бернулли

На этом примере мы познакомимся с методом замены переменных для решения уравнений, у которых в исходном виде решение записать нельзя.

Это уравнение имеет вид:

(1.35)

Полная характеристика уравнения будет следующая:

1. Порядок уравнения – 1.

2. Коэффициенты переменные – (p(x)).

3. Не линейное. Неизвестная функция y(x) в степени отличной от нуля и единицы.

Данное уравнение приводится к линейному с помощью подстановки (замены переменных), следующим образом:

. (1.36)

Разделим левую и правую часть (1.35) на .

(1.37)

Про дифференцируем по x выражение (1.36). Производную от y(x) вычислим как производную от сложной функции.

(1.38)

Используя выражения (1.36) и (1.38) из (1.37) получим:

(1.39)

Последнее выражение – это линейное не однородное уравнение

первого порядка. Общее решение такого уравнения (из (1.18)) будет:

Решение исходного уравнения найдём из условия (1.36).

Примеры.1. ; n=2; .

Разделим на и вычислим производные:

, .

В итоге получим линейное уравнение для переменной z(x).

.

Его решение будет:

. (1.40)

Решение для y(x) по (1.36) будет:

.

2.

По выражению (1.39) запишем уравнение для z(x):

По формуле решения линейного не однородного уравнения первого порядка запишем для z(x):

Общий интеграл для исходного уравнения по условию (1.36) будет:

1.7 Теорема существования и единственности решения задачи Коши

Т.к. не всегда можно получить решение для уравнения в явном виде, развились и активно используются (особенно с появлением ЭВМ) численные методы решения таких уравнений. Это приближённые методы и гарантия получения правильного результата может быть только в случае существования и единственности решения задачи Коши, т.к. численно решается именно эта задача.

Познакомимся с методом Эйлера для интегрирования уравнений указанного вида

. (1.41)

Его идея заключается в том, что точная интегральная кривая заменяется ломаной, кусочно – линейной функцией, каждый отрезок которой касается одной из интегральных кривых на одном из своих концов. Отрезок делится на n частей.

; - шаг дискретной сетки; - узел сетки. Для равномерной сетки . n-число шагов. - н.у. (заданы). На каждом шаге ломаной, производная остаётся постоянной. Последовательно вычислим значение во всех узлах сетки.

_…

……;

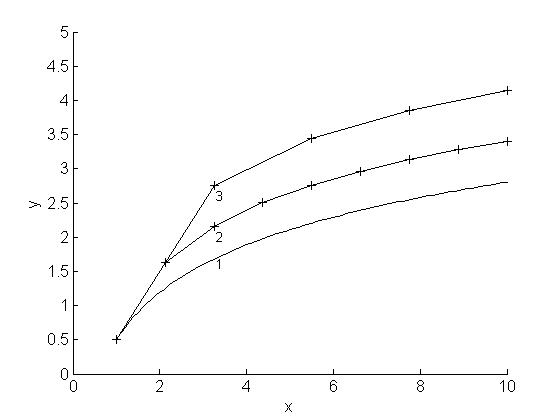
Рис.5. Ломаные Эйлера и точное решение

1 - точное решение; 2 – n=8; 3 – n=4

При , ломаная Эйлера приближается к искомой интегральной кривой и даёт всё более точное решение в точке . Доказательство этого факта приведёт нас к фундаментальной теореме о существовании и единственности решения уравнения в форме Коши, при и достаточно общих условиях, наложенных на .

ТЕОРЕМА. Дано:

непрерывна в ;

и удовлетворяет условию Липшица: N-const., (т.е. производная ограничена), то существует единственное решение в области уравнения (1.41)

которое удовлетворяет Н.У. , где

; в D.

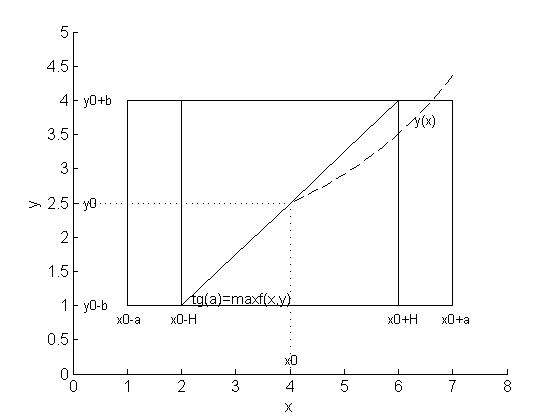
Рис.6. Область D и решение уравнения y(x)

Функция y(x) может выйти из области D через . Интегральная кривая не выйдет из области D при условии

,

где H наименьшее из чисел (a,b/M).

ДОКАЗАТЕЛЬСТВО.

Заменим уравнение (1.41) с Н.У. эквивалентным интегральным уравнением

(1.42)

Если (точное решение) обращает (при подстановке) (1.41) в тождество и удовлетворяет Н.У., то обращает в тождество и (1.42) и наоборот. Построим ломаную Эйлера , исходящую из с шагом , коэффициент наклона каждого звена < .

Проведём доказательство в три этапа.

1. Последовательность равномерно сходится к (точному решению).

2. Функция является решением интегрального уравнения (1.42).

3. Решение - единственное.

Доказательство 1. По определению при

k=0,…,n-1.

(1.43)

Т.к. f(x,y) непрерывна в D , получаем:

(1.43а)

при

; ; ;

Интегрируя (1.43) по x и учитывая, что получим:

(1.44а)

n – целое положительное число. При целом m>0

(1.44)

Вычитая из (1.44) (1.44а) получим

Учитывая (1.43а) и условие Липшица получим:

.

Тогда

Отсюда

Критерий Коши. верхний предел в интеграле.

Для >0, при достаточно больших , последовательность непрерывных функций непрерывно сходится при . .

Доказательство 2. Перейдём в (1.44а) к пределу при .

.

(1.45)

Т.к. равномерно сходится к непрерывна в D, последовательность

.

,

если .

Но это условие выполняется, если для всех x из

.

Так как , равномерно сходится к в (1.45) возможен переход к пределу под интегралом. Принимая, что

, а ,

получим, что и удовлетворяет интегральному уравнению.

Доказательство 3. Допустим, что есть два не совпадающих решения:

Вычитая тождества:

.

.

С учётом условия Липшица, получим:

.

Полученное неравенство противоречиво, если , т.к. по условию теоремы Противоречие снимается при , т.е. решение единственное. Интегральная кривая становится не продолжаемой, если нарушаются условия теоремы.

Пример 1.

Решение не продолжаемо, т.к. правая часть уравнения f(1,0) разрывная.

Пример 2.

Интегральная кривая продолжается до асимптоты

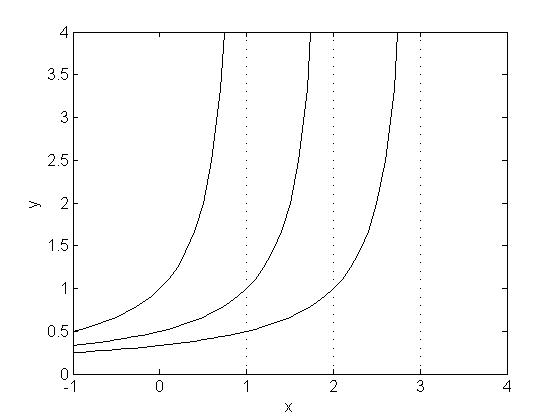
Рис.7. Решения примера 2 для разных НУ

При оценке существования и единственности решения задачи Коши, можно использовать (вместо условия Липшица) более грубую оценку: , т.е. частная производная ограничена.