Особые решения
При
делении на
мы можем потерять решения, определяемые
уравнениям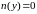и
и
.
Если
- корень
,
то при
для всех
имеем тождество
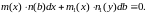
То
есть
–
решение исходного уравнения, т. к.
полностью отвечает этому определению
(
непрерывна для всех заданных
и обращает в тождество исходное уравнение,
т. к.
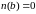и
– дифференциал константы). Если эти
решения не получаются из (1.12) при частных
числовых
,
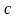то это особые решения. (Аналогично
при
).
Из решения
исключаем точку
,
т.к. при
и
одновременно в (1.11) не определён наклон
поля в точке
.
Других особых решений нет.
Пример. Дано дифференциальное уравнение
Выделить интегральную кривую, проходящую через точку (0,1), и найти особые решения.
Преобразуем исходное уравнение и проинтегрируем его:
.
Подставим
в общее решение
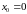и
и 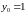получим решение в форме Коши (рис. 4):
Особые решения.
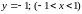
– исключаем
;
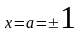– исключаем
.
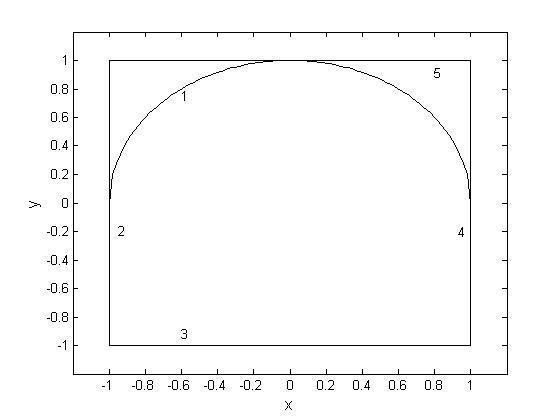
Рис. 4. Графики особых решений и задачи Коши
1-задача Коши; 2-5 особые решения
1.4 Линейные неоднородные уравнения
Это уравнения вида
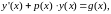(1.13)
где
и
зависят только от
и непрерывны в интервале
;
и
только в первой степени;
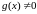-неоднородное
уравнение;
– однородное
уравнение.
Сначала построим общее решение линейного однородного уравнения:
(1.14)
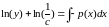
Так
как константу при вычислении неопределённого
интеграла можно задать в любой форме,
представим её как
:
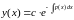(1.15)
Все решения (1.13) содержатся в (1.15). Подставим в (1.15) пределы интегрирования с переменным верхним пределом:
,
,
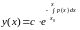Тогда
и общее решение в форме Коши имеет вид
.
Пример 1. Дано уравнение
.
Здесь
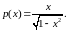
Тогда
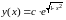- общее решение в области -
,
-1<
<1.
Пример
2. Рассмотрим
уравнение
.
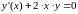Имеем
Решение определено на всей оси .
Свойства решений однородного линейного уравнения
Если
– частное решение (1.13), т. е.
,
то
,
(
-
константа) тоже является решением этого
уравнения:
.
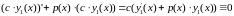Если
–
не нулевое частное решение (1.13) , то
– общее решение (1.13).
Теперь построим общее решение для неоднородного уравнения (1.13). Пусть – решение этого уравнения. Тогда
.
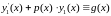Возьмём
некоторую функцию
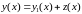и выясним, для каких
она будет решением неоднородного
уравнения. Подставим её в (1.13):
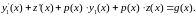
Так как
,
то
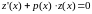
– соответствующее однородное уравнение, полученное из (1.13) при .
Тогда:
(1.16)
Все решения (1.13) содержатся в (1.16). Это общее решение неоднородного уравнения, где - общее решение соответствующего однородного уравнения.
Построим общее решение уравнения (1.13) методом вариации произвольной постоянной (метод Лагранжа). Запишем решение (1.13) в том же виде, что и соответствующего однородного уравнения:
(1.17)
Заметим,
что здесь
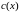– не константа, а функция независимой
переменной, причём такая, что (1.17)
становится решением исходной задачи
(1.13). Конкретный вид
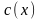пока не известен.
Раз это решение, то подставим его в исходное уравнение (1.13):
Тогда:
Подставим полученное выражение для в (1.17):
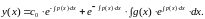(1.18)
Первое слагаемое – , т.е. общее решение соответствующего однородного уравнения; второе – , частное решение заданного неоднородного уравнения (1.13), а полностью в формуле (1.18) записано общее решение неоднородного уравнения (1.13).
Заменив
в (1.18) неопределённые интегралы на
определённые, с переменным верхним
пределом (для
и
),
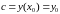получим общее решение уравнения (1.13) в
форме Коши (т.е. решение задачи с заданными
начальными условиями):
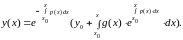(1.19)
Пример 1. Найдем решение неоднородного уравнения
.
Для этого уравнения имеем:
.
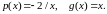
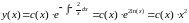Подставим полученное решение в исходное уравнение:
,
Тогда общее решение будет
.
Пример
2. Найдем
решение уравнения
.
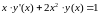Приведем уравнение к виду
.
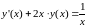Следовательно,
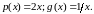Подставив
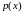и
в общее решение (1.18), получим
При решении этого типа уравнений часто используют метод подстановки, который мало чем отличается от метода Лагранжа. Запишем применение этого метода в общем виде.
Идея метода заключается в том, что решение неоднородного уравнения ищется в виде произведения двух функций:
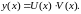
Раз решение, можно подставить его в исходное уравнение (1.13).
Или:
Одну из неизвестных функций можно
выбрать произвольно. Обычно это
причём её рассматривают как решение
дифференциального уравнения (выражение
в скобках в последней формуле):
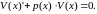
Нетрудно догадаться, что мы получили соответствующее однородное уравнение, и его решение будет:
Тогда, учитывая, что выражение в скобках =0, получим решение для U(x):
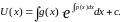
И общее решение исходного неоднородного уравнения будет (как и в методе Лагранжа):
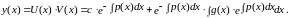
В
заключение этого параграфа заметим,
что в общем представлении уравнений,
разрешимых по отношению к производной
,
для линейных неоднородных уравнений
правая часть запишется в следующем
виде:
.
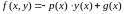