
- •Предисловие
- •Глава 2 содержит материалы по изучению методов аналитического решения линейных уравнений порядка n как однородных так и не однородных, построение их общего решения и задачи Коши.
- •Глава 1 дифференциальные уравнения первого порядка
- •1.1 Основные понятия и определения
- •1.2 Геометрическое истолкование решений Поле направлений. Интегральные кривые. Задача Коши
- •1.3 Уравнений с разделяющимися переменными
- •Особые решения
- •1.4 Линейные неоднородные уравнения
- •Свойства решений однородного линейного уравнения
- •1.5 Уравнения в полных дифференциалах
- •Признак уравнения в полных дифференциалах Построение общего интеграла.
- •Задача Коши.
- •Интегрирующий множитель
- •Краткий итог рассмотренных уравнений
- •1.6 Уравнение Бернулли
- •1.7 Теорема существования и единственности решения задачи Коши
- •Особые решения
- •Глава 2 дифференциальные уравнения порядка n
- •2.1 Основные понятия и определения
- •2.2 Фундаментальная система решений. Общее решение однородного лду. Задача Коши
- •2.3 Решение однородных лду порядка n с постоянными коэффициентами
- •2.4 Решение линейных неоднородных уравнений порядка n
- •2.5 Метод вариации произвольных постоянных(метод Лагранжа)
- •2.6 Метод неопределённых коэффициентов
- •2.7 Метод Коши
- •Контрольные вопросы
- •Глава 3 системы дифференциальные уравнения порядка n
- •3.1 Основные понятия и определения
- •Некоторые свойства решений однородной системы
- •3.2 Решение не однородной системы
- •3.3 Однородные системы уравнений с постоянной матрицей
- •3.4 Матричный метод решения сду
- •Характеристические числа действительные, разные
- •Характеристические числа комплексные
- •3.5 Автономные системы и их фазовые портреты
- •Глава 4 не линейные системы дифференциальных уравнений
- •4.1 Исследование качественной структуры
- •Фазового пространства в окрестности особых точек
- •4.2 Возможный характер простых состояний равновесия
- •1. . Корни действительные и одинаковых знаков: ;
- •Направления, в которых траектории стремятся к простым состояниям равновесия
- •Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия
- •4.3 Нелинейные консервативные системы
- •4.4 Уравнение Вольтера
- •4.5 Уравнения Гамильтона
- •Теорема Лиувиля
- •4.6 Предельные циклы и автоколебания
- •4.7 Уравнение Ван – Дер – Поля
- •4.8 Приближённый метод исследования предельных циклов
- •4.9 Некоторые признаки существования и отсутствия предельных циклов
- •Критерий Бендиксона отсутствия предельных циклов
- •4.10 Использование точечных отображений для изучения фазовых портретов
- •Список литературы
4.9 Некоторые признаки существования и отсутствия предельных циклов
Дана система ДУ:
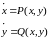 (4.15)
(4.15)
Гладким циклом однократного пересечения называется простая гладкая замкнутая кривая С, обладающая следующими свойствами:
На кривой С не лежит ни одного состояния равновесия.
Во всех точках кривой С траектории не имеют с ней касания и либо все входят внутрь, либо все выходят из области С.
Тогда, если С-цикл однократного пересечения,G ограниченная им область, принадлежащая области определения (4.15) и при этом:
1)все траектории, пересекающие С, при возрастании t входят в область G;
2)в области G имеется единственное состояние равновесия в т.(0,0), являющееся не устойчивым узлом или не устойчивым фокусом, то С устойчивый предельный цикл.
Критерий Бендиксона отсутствия предельных циклов
Если
в области G
выражение
 не меняет знак и не равно 0 тождественно,
то в этой области не существует замкнутых
контуров, составленных из траекторий.
не меняет знак и не равно 0 тождественно,
то в этой области не существует замкнутых
контуров, составленных из траекторий.
4.10 Использование точечных отображений для изучения фазовых портретов
На фазовой плоскости возьмём отрезок AB: (дуга без контакта, т.е. на ней нет особых точек и фазовые траектории не являются её касательными).
Пусть
дуга АВ- параметрическая кривая:
 ,
где S
параметр. Обозначим через S
координату произвольной точки Q
на АВ. Пусть x=x(t)
и y(t)
фазовые координаты траектории, проходящей
через точку Q.
С увеличением t
фазовая траектория снова пересечёт АВ
в точке Q+(параметр
S+).
Точка Q+
(первого следующего пересечения АВ той
же фазовой траекторией) называется
последующей
по отношению
к исходной точке Q.
Рис.33.
,
где S
параметр. Обозначим через S
координату произвольной точки Q
на АВ. Пусть x=x(t)
и y(t)
фазовые координаты траектории, проходящей
через точку Q.
С увеличением t
фазовая траектория снова пересечёт АВ
в точке Q+(параметр
S+).
Точка Q+
(первого следующего пересечения АВ той
же фазовой траекторией) называется
последующей
по отношению
к исходной точке Q.
Рис.33.
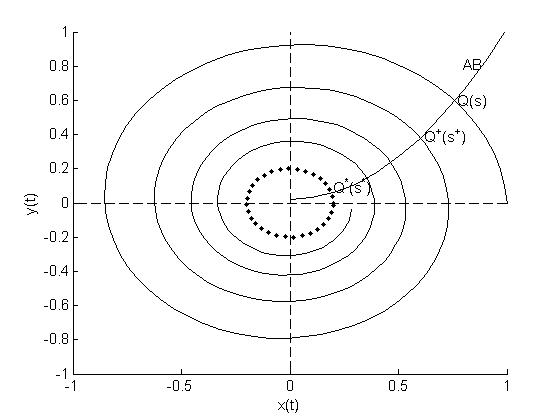
Рис. 33. Построение точечных отображений
Зависимость S+ =f(S) последующего значения параметра, при пересечении фазовой траекторией дуги АВ от предыдущего в силу решения уравнения (1), называется функцией последования. Она определяет закон точечного преобразования для данной не линейной системы.
Для функции последования справедливо следующее:
1)функция последования, для аналитической системы (4.15),тоже является аналитической функцией;
2)производная от функции последования всегда больше 0. Это является следствием того факта, что траектории не пересекаются.
Возможен случай, когда последующая точка Q+ совпадёт с исходной Q, т.е. f(s) =s=s*. При этом мы получаем замкнутую фазовую траекторию (предельный цикл или кривую соответствующую особой точке «центр»). Это траектория L0 на Рис.33 показана точками. Рассмотрим последовательные точки пересечения с АВ другой траекторией L.
L пересекает АВ в точках S1…Sn.
При этом S2=f(S1); S3=f(S2); …Sn+1=f(Sn). 4.16
Если L→L0 при t→∞ , то последовательность 4.16 стремится к S* . Не подвижная точка S* отображения S+=f(S) называется устойчивой, если существует такая её окрестность, что все последовательности 4.16 с начальным значением S1 в её окрестности → к S* (и наоборот –не устойчивые). Таким образом, наличие устойчивых или не устойчивых точек последовательности 4.16 говорит о наличии устойчивого или не устойчивого предельного цикла. Неподвижная точка отображения S+ =f(S*) устойчива, если производная в ней f ‘(S*)<1 и не устойчива при f ‘(S*)>1. Точка пересечения биссектрисы и f(S) − S*. Производная в точке S1* меньше 1, и предельный цикл устойчивый Рис.34.а.
В точке S2* f ‘ (S*)>1 и предельный цикл не устойчивый. Рис. 34.б.

Рис.34. Диаграмма Ламерея
Пример.
Дано уравнение

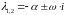
Общее решение будет:
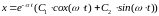 .
.
Для Н.У. t0=0; C2=0; x(0)=C1=x0.
Тогда решение в форме Коши будет:
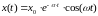 .
.
Дуга АВ совпадает с осью x. Тогда:
 .
.
T-период, через который фазовая траектория пересекается с АВ (в нашем случае с осью x, и S=X).
Тогда

и особая точка – устойчивый фокус.

Рис.35. Функция последования точечного отображения
На Рис.35 показана функция последования для данного примера.
