4.3 Нелинейные консервативные системы

Рассмотрим уравнение движения (из механики):

(4.4)

Запишем это уравнение как систему:

.

Тогда полная энергия для такой системы будет:

для m=1.

Для линейного осциллятора ;

.

При этом .

Полная производна . .

Из (4.4) получим:

. (4.5)

Для W=C получим, фактически, фазовую траекторию .

_Пример. . Из (4.5), для _,

Построим графики полученных функций в соответствующих осях :

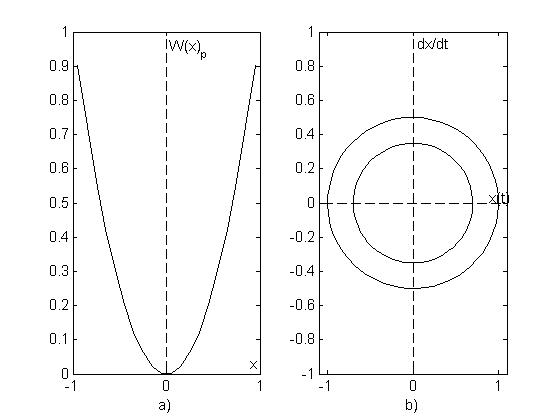
Рис.23.a – потенциальная функция, b – фазовые траектории

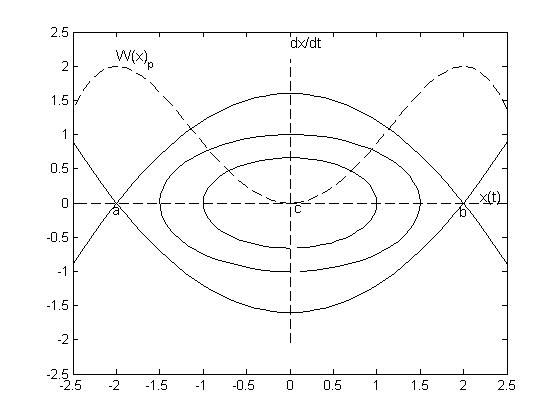
Рис.24. W(x) – потенциальная функция для

a(-2,0), b(2,0) – особые точки типа «седло»

c(0,0) – особая точка центр

Для кубической нелинейной функции , построенные и фазовые траектории, показаны на Рис.24.

4.4 Уравнение Вольтера

Для многих задач понятие «энергия» (кинетическая или потенциальная) трудно определить. Рассмотрим подробно поведение решений на фазовой плоскости уравнения Вольтера, описывающего динамику изменения взаимодействующих популяций хищников и травоядных.

где: –число вегетарианцев; –число хищников; –коэффициент размножения вегетарианцев; –коэффициент смертности хищников; –коэффициент смертности вегетарианцев; –коэффициент размножения хищников. –один из способов моделирования взаимодействия переменных.

1.Система уравнений для нахождения координат осбых точек:

.

Координаты первой точки (0,0).

,

Тогда координаты второй точки:

. (4.6)

Линеаризуем уравнения вблизи особых точек. Для этого разложим правые части дифференциальных уравнений в ряд Тейлора и оставим только линейные члены.

.

Тогда определитель линеаризованной системы будет . Система вблизи особой точки (0,0) примет вид:

.

Значения характеристических чисел будет: .Тип этой особой точки будет седло т.к. и >0.

Определитель системы ДУ, линеаризованной вблизи второй особой точки (4.6) будет:

.

После подстановки значений координат особых точек из (4.6), определитель и характеристические числа для этого случая будут:

; .

Корни получились чисто мнимые и тип особой точки будет центр. Т.е. траектории замкнутые. Получим их.

Рассмотрим поведение системы для больших значений фазовых координат.

В этом случае линейными членами (ввиду их малости по сравнению с не линейными) можно пренебречь.

Преобразованная таким образом система примет вид:

. (4.7)

.

Таким образом, для больших значений фазовых координат, траектория близка к прямой. Полностью фазовый портрет получим при интегрировании исходной системы уравнений с заданными параметрами и начальными условиями для нормированных переменных .Рис.25.

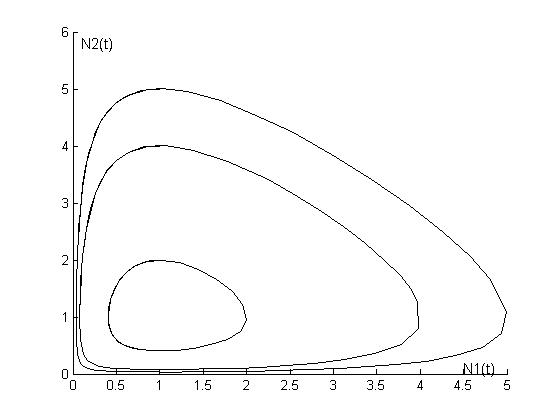
Рис.25. Отображение решений уравнения Вольтера

на фазовой плоскости

Найдём первый интеграл системы (4.7). До множим эти уравнения на и сложим их:

. (4.8)

Умножим исходные уравнения на и сложим их:

. (4.9)

Из (4.8) вычтем (4.9)

.

Полученное выражение умножим на dt и проинтегрируем:

.

Получили первый интеграл исходной системы. Функция - первый интеграл системы ДУ, если она постоянна вдоль каждого решения системы. Для n=2 первый интеграл даёт уравнение фазовых траекторий на плоскости

.

На Рис.26 показаны их проекции на плоскость (N1,N2).

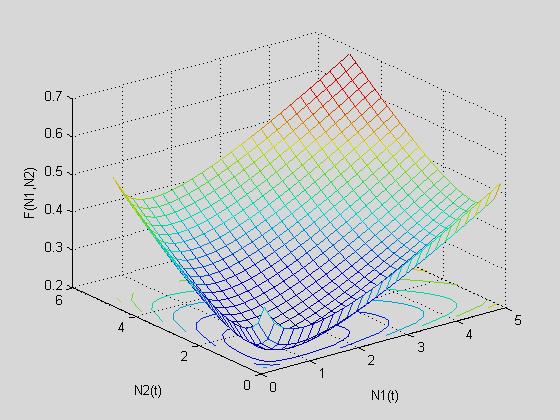
Рис.26. Первый интеграл для уравнения Вольтера и проекция фазовых

траекторий на плоскость (N1,N2)

Фазовые траектории для консервативной системы замкнутые кривые, если С не соответствует критическим точкам на поверхности . Критической точке на поверхности соответствуют особые точки ДУ. В системе с первым интегралом имеются особые точки только типа «центр» и «седло». Точка (1,1) – центр , (0,0) – «седло». Рис.26.

Лемма Морса.

В окрестности не вырожденной критической точки поверхности , можно ввести дифференцируемую замену координат

( )

такую, что в окрестности этой точки

будут кривыми второго порядка . центр; седло.

Таким образом, при определении консервативной системы (при сохранении W(t)=C), ясно, что

– первый интеграл уравнения движения.

Система консервативна, если:

.