3.4 Матричный метод решения сду
Предварительные замечания.
Мы уже раньше в вели понятие фундаментальной матрицы решений (таблицы решений). Кроме того и сама СДУ то же может быть записана в матричной форме. Вспомним правила выполнения некоторых операций над матрицами.
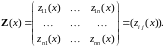
Тогда производные от Z(x) в точке x=x0
.
Т.е. дифференцирование матриц сводится к дифференцированию всех её элементов.
Некоторые правила дифференцирования.
Если
,
то
Альфа
– число.
Сомножители нельзя переставлять.
;
;
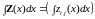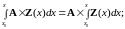
Экспоненциальная функция от матрицы Z.
Если
,
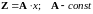то матричный ряд будет:
Для
случая, когда
коммутирует с
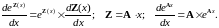
Пусть
,
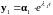(3.18)
где t независимая переменная.
н.у.
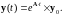(3.19)
Подставим (3.19) в исходную систему уравнений:
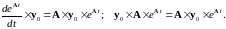
т.е. это решение исходной СДУ.
Таким
образом, один из способов решения СДУ
с постоянной матрицей – матричный ряд,
умноженный на
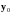(это приближённое решение). Если найти
предел ряда, то это будет аналитическое
решение задачи Коши.
Как
вычислить операторную экспоненту, чтобы
получить фундаментальную матрицу
решений? Для частного случая
-
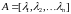диагональная матрица, а
собственные числа матрицы, получим:
.
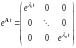Если А не диагональная?
Характеристические числа действительные, разные
Дано
уравнение
.
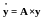Сделаем замену переменных
-
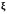переменные в собственном базисе.
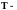неизвестная
невырожденная матрица, преобразующая
переменные из собственного базиса в
базис исходных переменных.
Получаем
систему с новой матрицей
Самый
простой вид В
– диагональная. Это получается при
условии, что столбцы матрицы Т
собственные вектора матрицы А.
.
В этом случае решение для
запишется в виде
,
или в матричной форме
.
Для
получения решения
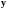сделаем линейное преобразование
.
Пример.
;
.
.
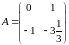Найдём собственные вектора:
.
Тогда решение в собственном базисе будет:
.
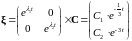Построим
матрицу Т и запишем решение для исходных
переменных:
;
.
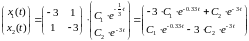Построим
фазовые траектории в собственном базисе
на плоскости
и на плоскости
.
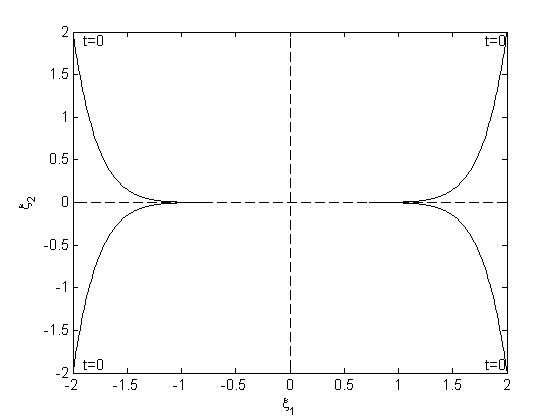
Рис.13. Устойчивый узел в собственном базисе
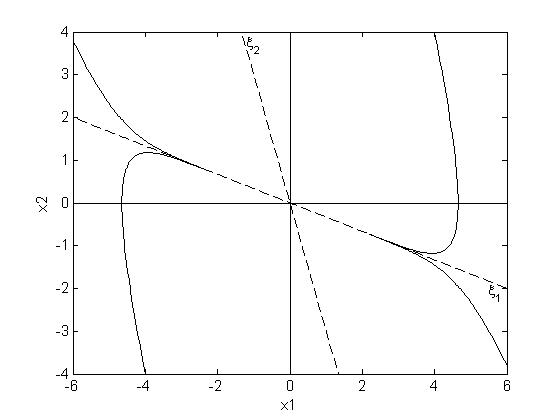
Рис. 14. Устойчивый узел в базисе исходных переменных
Пусть собственные числа матрицы А действительные и кратные. Элементы матрицы А– константы.
.
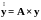Введём
новую переменную
,
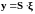где S
не вырожденная матрица. Запишем новую
систему ДУ.
;
.
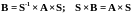Ясно, что В должна быть простой, но не чисто диагональной, т.к. решениями являются линейно зависимые функции и собственные вектора одинаковые.
Матрица В это действительная Жорданова форма матрицы А имеет квази диагональную форму и состоит из клеток Жордана. Правила построения такой матрицы следующие:
Тогда клетки Жордана для корней разной кратности будут:
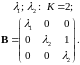
Клетку
Жордана можно представить в виде
,
где Е– единичная матрица.
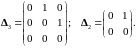
Пусть К=2. Тогда СДУ в собственном базисе будет , а общее решение в собственном базисе запишется (при разложении матричной экспоненты в ряд) в следующем виде:
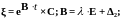
Общее решение в собственном базисе.
Для
построения решения в базисе исходных
переменных из матричного уравнения
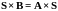найдём элементы матрицы S.
После умножения матриц приравняем
(поэлементно) выражения слева и справа.
Решив полученную СЛАУ, найдём матрицу
S.
Пример.
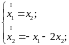
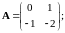
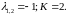
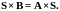
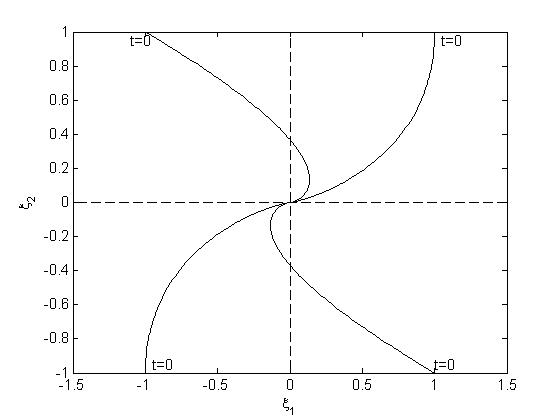
Рис.15. Фазовый портрет в собственном базисе
Устойчивый вырожденный узел
;
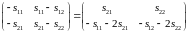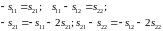
Доопределим
.
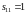Тогда
;
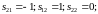
Общее решение исходного уравнения.
Построим фазовые траектории решений в базисе исходных переменных.Рис.16.
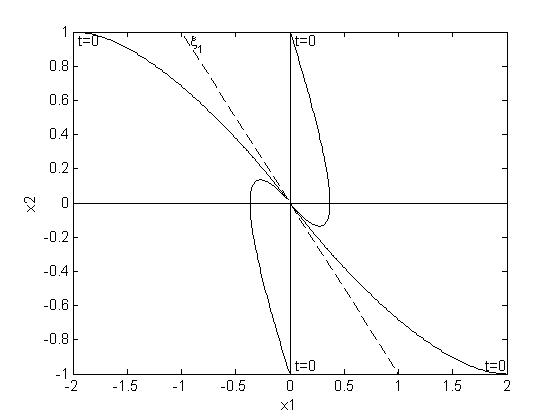
Рис.16. Фазовый портрет в базисе исходных переменных
Устойчивый вырожденный узел
Рассмотрим на примере СДУ построение общего решения для случая, когда кратные корни являются простыми делителями.
ПРИМЕР
1.
.
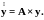
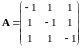Характеристический полином и его корни будут:
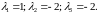
Вычислим собственные вектора для найденных корней:
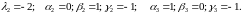
Это
вырожденный случай. Хотя корни кратные,
но при этом они образуют простые делители
,
а не
.
Решение в этом случае ищется не в виде
,
а как для случая действительных разных корней.
Жорданова форма матрицы А будет чисто диагональной:
.
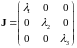Тогда решение в исходном базисе запишется как:
.
Столбцы матрицы S из собственных векторов матрицы A.
.
Вронскиан
функций образующих ФМР
,
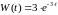т. е. функции эти линейно не зависимые.
Если имеем несколько кратных корней вида:
.
.
.
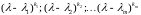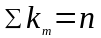Жорданова матрица станет квази диагональной, а на главной диагонали запишутся клетки Жордана размерностью Кi*Кi.