3.2 Решение не однородной системы

(3.6)

Сначала находим общее решение однородного уравнения (3.3):

Общее решение не однородного уравнения запишется как сумма частного решения не однородного уравнения и общего решения соответствующего однородного.

Сначала запишем общее решение однородного уравнения, но при этом будем считать коэффициенты не константами, а некоторыми функциями не зависимой переменной. При этом таковы, что общее решение однородной ситемы уравнения, становится общим решением не однородной СДУ.

– фундаментальная матрица.

Подставим это решение в исходное уравнение (3.6) и получим

;

где: – общее решение однородной системы.

– частное решение не однородной системы при нулевых Н.У.

3.3 Однородные системы уравнений с постоянной матрицей

(3.7)

Для простейших систем уравнений можно использовать метод приведения системы порядка N, к уравнению N-го порядка.

Пример. .

Продифференцируем первое уравнение:

Из первого уравнения найдём второе решение

и запишем решение в векторной форме:

Для построения общего решения системы (3.7) достаточно найти хотя бы одну фундаментальную систему решений.

Мы покажем, что фундаментальная система решений может быть построена из элементарных функций, голоморфных в интервале (a,b).

По аналогии с однород­ным линейным уравнением с постоянными коэффициентами будем искать частное решение системы (3.7) в виде

(3.8)

где — некоторые постоянные числа, причем числа одновременно, ибо в про­тивном случае мы получили бы очевидное нулевое решение, которое не может входить в состав фундаментальной системы и, следовательно, не может быть использовано для построения общего решения.

Обратим особое внимание на то, что число мы берем одно и то же для всех функций, составляющих решение.

Подставляя функции (3.8) в систему (3.7), сокращая на и перенося все члены направо, получим для определения чи­сел следующую систему:

(3.9)

Нас интересует ненулевое решение этой системы по отношению к . Такое реше­ние существует лишь при условии, что определитель системы равен нулю, т. е.

(3.10)

Уравнение (3.10) называется характеристическим уравнением си­стемы (3.7), его корни – характеристическими числами, а опре­делитель– характеристическим определителем.

Рассмотрим сначала случай, когда все характеристические числа действительные и разные.

1. Подставим это выражение в систему (3.7):

Е – единичная матрица. – выражение (3.10) в матричной форме. При : , –собственный вектор для данного . Заметим, что ищется с точностью до константы.

Для частного случая n=2:

Построение фундаментальной системы решений и общего решения однородной линейной системы.

1. Корни характеристического уравнения действительные различные.

Подставим в (3.8) и получим:

(3.11)

Таким образом, если действительные разные, система имеет n вещественных, линейно независимых решений, образующих матрицу решений (3.11).

Тогда (суммируя по столбцам) запишем общее решение исходной системы (3.7):

(3.12)

Заметим, что находятся с точностью до константы.

Пример.

Пусть , тогда

Зададим , тогда

Построим таблицу решений:

Тогда общее решение будет:

Решение получено суммированием по столбцам. В общее решение для каждой функции входят функции для всех (i=1;…n).

y₁ и y₂ – фазовые координаты в базисе исходных переменных. Координаты – в собственном базисе.

_{Рис.9. Решение для} и Рис.10. Фазовая плоскость для и

Построим оси ξ1 и ξ2 в базисе исходных переменных y1 и y2.

Пусть c2=0. Тогда, используя матрицу перехода из собственного базиса в базис исходных переменных, наёдём значения координат с1 в системе (y1,y2). Через начало координат и найденную точку построим ось ξ1 (пунктирная линия) в системе координат (y1,y2). Аналогично построим ось ξ2 и фазовые координаты в базисе исходных переменных.

Рис.11. Фазовый портрет с особой точкой «седло»

2.Характеристические числа комплексные.

Если корни комплексные, то они имеют и сопряжённый корень:

.

Будем (как и в предыдущем случае) искать решение в виде:

(3.13)

- комплексные числа. Сопряжённый корень не рассматриваем при построении Ф,С,Р., т.к. он не порождает новых, линейно независимых решений. Выделяя из этих комплексных решений действительную и мнимую части, мы получим 2-а вещественных, линейно не зависимых решения. Запишем подробно выкладки для одного решения:

– собственные вектора, полученные при решении системы уравнений:

Теперь построим Ф.С.Р. для данного

(3.14)

Если для системы n=3 имеем корни ; , то Ф.С.Р. будет (из (3.14)): .

_{Общее решение получим суммируя функции по столбцам (с пост}оянными коэффициентами):

_{Самостоятельно для .}

Пример.

Пусть тогда

Задача Каши

Число н.у. – . Н.У. – значение всех функций в точке = –(независимая переменная).

Подставив Н.У. в общее решение, найдём значение произвольных коэффициентов и запишем решение в форме Коши.

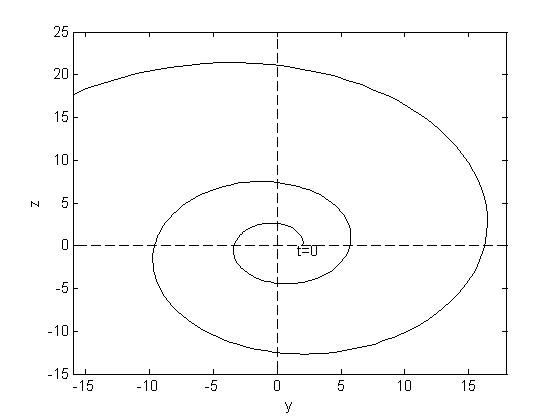
Рис.12. Неустойчивый фокус

Тогда решение задачи Коши отобразится на фазовой плоскости (y,z) как расходящаяся траектория. Рис.12.

3. Корни кратные.

Пусть кратный корень. Тогда решение ищется в виде (для частного случая, когда число собственных векторов K-1):

(3.15)

полином степени (К-1). Всего неизвестных коэффициентов (K*n). Причём среди всех этих коэффициентов полиномов К - произвольных. Выразив все остальные коэффициенты через эти произвольные, построим К линейно независимых решений Если корень действительный, то и решения действительные. Если (т.е. комплексный и кратный К) найдём К комплексных линейно не зависимых решений, которые порождают 2К действительных линейно не зависимых решений.

Если (3.15) решение заданной системы, то подставим его в исходную СДУ, затем прировняем коэффициенты при одинаковых функциях и, с учётом указанных выше условий (для К коэффициентов), решим полученную систему алгебраических уравнений по отношению к неизвестным (K*n-K) коэффициентам.

Пример. x(t); y(t); z(t). ;

P- характеристический полином, α- собственные вектора.

Тогда первая строка в таблице решений, для корня действительного разного, запишется в следующем виде:

(3.16)

Решения для кратных корней (по 3.15) будет получено в следующем виде:

Подставим записанные решения в виде полиномов в исходную систему уравнений, сократим на и приведём подобные.

Приравняем коэффициенты при одинаковых функциях слева и справа от знака равенства:

При t:

Выберем коэффициенты С как произвольные и выразим остальные через них.

Тогда решения запишутся в следующем виде:

Теперь, задав (затем наоборот), построим с учётом (3.16) фундаментальную матрицу решений:

Умножив транспонированную фундаментальную матрицу решений на вектор произвольных коэффициентов, получим общее решение СДУ с постоянными коэффициентами.

; (3.17)

Рассмотрим, в более общем виде проблему решения СДУ для кратных корней.

Пусть для матрицы А имеем К – кратный корень, при этом К линейно не зависимых векторов. (В предыдущем примере мы не искали собственные вектора, но он для той системы один). Тогда этому корню соответствует К линейно не зависимых решений:

То есть мы получили выражение как для случая действительных разных корней.

Пример.

Для

Тогда фундаментальная матрица решений будет:

Умножив фундаментальную матрицу на вектор произвольных коэффициентов, получим общее решение СДУ.

Если для корня кратности , собственных линейно не зависимых векторов m (причём m<K), то решение ищется в виде:

Рассмотрим более общий метод решения систем ЛДУ с постоянной матрицей.