МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

А.В. Козловских

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ

УРАВНЕНИЯ

(Исследование методов решений с помощью MAPLE и MATLAB)

Рекомендовано в качестве учебного пособия

Редакционно-издательским советом

Томского политехнического университета

Издательство

Томского политехнического университета

2012

УДК519.62

ББК (В)22,1

Э18

Козловских А.В.

Э18 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (Исследование методов решений с помощью MAPLE и MATLAB): учебное пособие / А.В. Козловских; Томский политехнический университет. – Томск:

Изд-во Томского политехнического университета, 2012. –168 с.

Данное учебное пособие представляет собой весьма полный современный курс обыкновенных дифференциальных уравнений. Подробно освещены все методы, изучаемые в классических вводных курсах, включая применение матричных методов, степенных рядов. В пособие включён раздел анализа решений методом фазовой плоскости как линейных, так и не линейных систем уравнений. Излагаются основы качественной теории дифференциальных уравнений. Для изучения всех этих методов автор использует самые современные математические пакеты: MAPLE, MATLAB. Для каждого из разделов в приложениях, на конкретных примерах, излагается методика применения математических пакетов. Несомненно, книга будет полезна всем, кто изучает дифференциальные уравнения – как математикам, так и студентам других специальностей.

УДК519.62

ББК (В)22,1

Рецензент

Доктор физико-математических наук, профессор ТГАСУ

Б.М. Шумилов

© ФГБОУ ВПО НИ ТПУ, 2012

© Козловских А.В.

© Оформление. Издательство Томского политехнического университета,2012

Предисловие

Пособие состоит из четырёх глав и трёх приложений.

Глава 1 посвящена изучению разных типов дифференциальных уравнений первого порядка и методам их решения. Рассматриваются основные задачи интегрирования ДУ и теорема существования и единственности решения задачи Коши.

Глава 2 содержит материалы по изучению методов аналитического решения линейных уравнений порядка n как однородных так и не однородных, построение их общего решения и задачи Коши.

В главе 3 излагаются методы исследования решений систем ДУ с постоянной матрицей: метод Эйлера и матричный метод построения фундаментальной матрицы решений; представление приближённого решения в виде матричного ряда; построение переходной матрицы (решение в матричной форме задачи Коши).

Глава 4 посвящена изучению анализа решений методом фазовой плоскости как линейных, так и не линейных систем уравнений. Излагаются основы качественной теории дифференциальных уравнений. Для изучения всех этих методов использует самые современные математические пакеты: MAPLE, MATLAB.

Приложение состоит из 3 разделов, каждый из которых содержит несколько лабораторных работ, в которых на конкретных примерах, излагается методика применения математических пакетов для изучения и применения разных методов интегрирования ДУ и их систем.

В приложении 1включены три лабораторных работы посвящённые изучению стандартных функций пакета MAPLE и методике их применения для решения математических задач, лежащих в основе изучаемых методов интегрирования ДУ.

Приложение 2 состоит из двух лабораторных работ. В этих работах изучается методика построения общего решения и задачи Коши для однородных и не однородных ДУ высокого порядка (N=4;5) в пакете MAPLE.

В приложении 3 первая работа посвящена освоению стандартных функций пакета MAPLE для нахождения общего решения и задачи Коши уравнений не только с постоянными коэффициентами, но и с переменными, а также даются примеры решения краевых задач.

В последней лабораторной работе демонстрируется решение не линейных ДУ численными методами в пакете MATLAB.

Книга будет полезна всем, кто изучает дифференциальные уравнения – как будущим специалистам по прикладной математике, так и студентам других специальностей.

Глава 1 дифференциальные уравнения первого порядка

1.1 Основные понятия и определения

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одной или нескольких переменных, причём в уравнения входят не только сами функции, но и их производные:

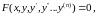(1.1)

где – независимая переменная (по ней производится дифференцирование);

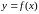– не известная функция (зависимая переменная);

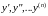– производные от по .

Если неизвестная функция зависит от одной независимой переменной, то это обыкновенные дифференциальные уравнения. Эти уравнения и рассматриваются в данном пособии.

Дадим определение некоторых терминов и понятий, которыми будем пользоваться в дальнейшем.

Порядок старшей производной в (1.1) определяет порядок дифференциального уравнения. В случае имеем уравнение первого порядка. Причём мы будем изучать такие уравнения, где независимая переменная и искомая функция представляются вещественными.

При изучении дифференциальных уравнений (ДУ) основной задачей является нахождение всех решений ДУ и изучение свойств этих решений. Когда говорят "решить ДУ", то это означает проинтегрировать данное уравнение.

Термин “проинтегрировать” понимают двояко:

1. В самой узкой постановке: записать выражение для искомой функции через элементарные:

.

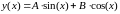Далеко не всегда это удаётся сделать.

2. Общая постановка задачи нахождения решения: уравнение считается решённым, если оно приведено к квадратурам, т. е. операциям взятия неопределённого интеграла.

Линейное ДУ – это такое уравнение, в котором неизвестная функция и все её производные только в первой степени и не являются аргументами других функций. Линейное ДУ с переменными коэффициентами называется такое уравнение, в котором коэффициенты при неизвестной функции и всех её производных являются функциями независимой переменной.

По общему выражению (1.1) запишем

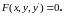(1.2)

Изучение разных видов ДУ первого порядка начнём с уравнений, разрешимых относительно производной. Из выражения (1.2) получим:

.

В теории ДУ используют разные формы их представления:

1. «Перевёрнутое» уравнение:

(1.3)

Это представление используется в окрестности точек, где .

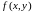2. Иногда целесообразно (1.2) представить в виде

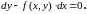(1.4)

Здесь 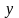и равноправные переменные, любую из них можно принять как независимую.

3. Если (1.4) умножить на некоторую функцию 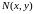, получим симметричное уравнение:

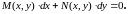(1.5)

Дадим подробное определение такого важного понятия, как решение дифференциального уравнения.

Пусть в (1.2) определена на подмножестве A вещественной плоскости 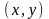, т. е. непрерывна вместе со своими частными производными в каждой точке из A. Тогда определённый в интервале 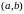, будет решением (1.2) , если:

1. существует производная 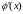для всех на , т.е. непрерывна на ;

2. функция обращает (1.2) в тождество , справедливое для всех на интервале , т. е. для любого на точка принадлежит A.

Примеры.1. Пусть , , Покажем, что является решением данного уравнения. Для этого подставим заданную функцию и её производную в уравнение и получим тождество:

.

Таким образом, функция обращает уравнение в тождество для , т. е. на всей оси .

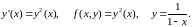2. Пусть Тогда