
- •Содержание
- •Глава 1. Домашнее задание - важнейшее звено процесса обучения, воспитания и развития личности школьника §1. Роль домашнего задания в развитии личности учащегося
- •§2. Домашнее задание - необходимая часть процесса обучения
- •§3. Виды домашних заданий
- •Глава 2. Пути повышения эффективности домашней работы учащихся
- •§1. Методика конструирования, постановки и контроля домашнего задания при обучении математике
- •§2. Взаимосвязь домашнего задания с изучением нового материала
- •§3. Дифференцированный подход при организации домашней работы
- •§4. Домашние задания творческого характера
- •§5. Повышение интереса учащихся к математике через домашние задания занимательного характера
- •Заключение
- •Список литературы
§4. Домашние задания творческого характера
В Законе Российской Федерации "Об образовании" в качестве высшей цели образования определено становление саморазвивающейся и самоопределяющейся личности, способной к открытому, творческому взаимодействию с окружающей природой, обществом, государством на основе общепринятых гуманистических ценностей общества.
Педагогическая наука рассматривает влияние образования на творческое развитие личности как на одну из центральных проблем. Педагоги отмечают важность единства обучения и воспитания в образовательном процессе с учетом интересов, способностей, возможностей и потребностей ребенка; большое внимание уделяется индивидуальному подходу в работе со школьниками, созданию условий для их саморазвития, самореализации как во время учебных занятий, так и в свободное время. И в современный период, всесторонне рассматривая эти проблемы, одной из приоритетных задач педагогической науки является простраивание качественно новых отношений между личностью и обществом, поиск наиболее оптимальных путей воспитания, обучения, творческого развития личности ребенка [1].
Особое значение для творческого развития ребенка имеют возможности, предоставляемые ему в детстве, в школьные годы. Здесь закладывается фундамент личности, формируются базовые социальные установки, основы мировоззрения, привычки, развиваются познавательные способности, складываются отношения с окружающим миром.
Однако, совершенно очевидно, что такая задача не может быть выполнена усилиями одной только школьной системы. Огромную роль в ее решении играет семья, окружение, средства массовой информации.
Одним из эффективных путей решения проблемы творческого развития личности ребенка выступает реализация личностно-ориентированного подхода, способного сыграть значительную роль в достижении школьником вершин своего творческого развития, определении жизненного пути.
Методические приемы обучения должны предусматривать увеличение доли самостоятельной деятельности учащихся, поощрение их инициативы. Большое внимание при этом желательно уделять домашним заданиям, которые ученики выполняют в основном самостоятельно. Как уже говорилось, потому, как её выполняют учащиеся и какие результаты они получают, можно судить об уровне овладения ими изучаемым материалом. Учителю бывает непросто определить объем домашнего задания и время, необходимое для его выполнения, в силу неоднородности класса и по способностям, и по предварительной подготовке. Возникает необходимость в составлении индивидуальных заданий, так как при ориентации на среднего ученика не используются полностью творческие возможности сильных учащихся. В то же время индивидуализация домашних заданий путем увеличения числа задач и упражнений для сильных учащихся исключает возможность проверки в классе тех задач, которые были даны дополнительно, так как основная часть класса этих задач дома не решала.
Более ценным и в методическом отношении представляются домашние задания, которые являются общим для всего класса, но содержат дополнительные вопросы или задачи, расширяющее их основное содержание.
Приведем несколько таких заданий, обозначая буквой А упражнение, обязательное для всего класса, а буквой Б его усложненный вариант творческого характера.
№ 1.
А. Выполните действия:
(4
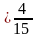 +
+
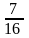
 ):
4
):
4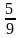 .
.
Б. Используя предыдущий результат, вычислите устно:
(4
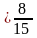 +
+
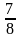 ):
4
.
):
4
.
В упражнении Б учащиеся должны вспомнить, как изменяется произведение при увеличении в 2 раза одного из сомножителей и как изменяется сумма при увеличении каждого слагаемого в 2 раза. Проверка такого задания вызывает общий интерес, у ребят появляется желание попробовать свои силы на более трудном задании.
№ 2.
А. Решите уравнения:
а) х - 21х + 104 = 0; б) х - 15х + 56 = 0; в) х - 3рх + 2р + 6 = 0.
При каких значениях р уравнение в) имеет решение?
Решение
примера в) заканчивается указанием на
то, что D
= р
- 24
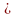 0
и уравнение имеет решение при р
24.
Значение параметра р
принадлежат объединению промежутков
(-
0
и уравнение имеет решение при р
24.
Значение параметра р
принадлежат объединению промежутков
(-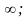 - 2
- 2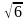 ]
]
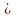 [ - 2
;
+
[ - 2
;
+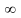 ).
).
Б. Решите в натуральных числах уравнение: х - 3ху + 2у + 6 = 0.
Решение.
Будем считать у параметром. Тогда D
= у
- 24. Значение D
должно быть точным квадратом. Следовательно,
уравнение у
- 24 = k
нужно решить в натуральных числах: у
- k
= 24, (у + k)
(у - k)
= 24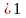 =
12
= 8
= 6
.
Это дает четыре системы линейных
уравнений, из которых только две имеют
решение в натуральных числах.
=
12
= 8
= 6
.
Это дает четыре системы линейных
уравнений, из которых только две имеют
решение в натуральных числах.
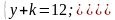 у = 7; х
- 21х + 104 = 0.
у = 7; х
- 21х + 104 = 0.
Отсюда х = 8 или х = 13.
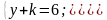 у = 5; х
- 15х + 56 = 0.
у = 5; х
- 15х + 56 = 0.
Получаем х = 7 или х = 8.
Исходное уравнение имеет в натуральных числах четыре решения: (8;7), (13;7), (7;5), (8;5).
Разумеется, задания творческого характера даются не каждый день, но они вызывают живой интерес всего класса, Учащиеся ждут эти задания. Большую роль в создании творческого начала в деятельности учащихся играют так называемые оригинальные домашние задания. К таким заданиям можно отнести: заполнить пропуски в последовательности чисел, которые получаются в результате действий указанных после текста; задания связанные с жизненными ситуациями, физическими явлениями, историческими событиями - такого рода задания вызывают огромный интерес у учащихся и несомненно носят творческий характер.
Приведу несколько примеров таких заданий.
1. 5 класс, тема "Действия над натуральными числами".
Каждому ученику предлагается карточка с текстом, В тексте пропуски, в них надо поставить числа - результаты выполнения заданий, указанных после текста. Пропуски заполняются в том порядке, в каком следуют друг за другом задания.
Все карточки посвящены теме "Числовые великаны вокруг и внутри нас". Вот текст одной из них:
"Древние люди говорили: "Звезд на небе как песчинок на морском берегу". В старину не было телескопов, а простым глазом мы видим на небе всего около …звезд. Подсчитано, что число песчинок на берегу моря в миллион раз больше, чем звезд, доступных невооруженному глазу.
Величайшие числовой гигант скрывается в воздухе, которым мы дышим. Каждый кубический сантиметр воздуха (это примерно объем воздуха в одном наперстке) заключает в себе … квинтиллионов мельчайших частиц, называемых молекулами. Если бы на свете было бы столько людей, сколько молекул воздуха в наперстке, то для них буквально не хватило бы места на нашей планете.
Если каплю крови рассмотреть в микроскоп, то в ней станут, видны очень мелкие тельца красного цвета. В 1 мм крови, то есть в одной капле, заключается примерно … красных телец. Сколько же всего их в вашем теле? Если вы весите 40 кг, то в вашей крови примерно… триллионов красных кровяных телец. Представим себе, что эта армия кружочков выложена в ряд друг за другом. Длина такого ряда составила бы … км. Нитью такой длины можно было бы обмотать земной шар по экватору более … раз".
Задания:
) 3845:
(10110 - 241)
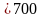 ,
,
) 346 -
(2486 + 335104: 476): 10,3) 507792: 596 + 870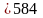 +58093
+58093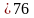 ,
,
) 708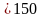 :
450 - 221,5) 2035 + 98765 + 11088: 132
:
450 - 221,5) 2035 + 98765 + 11088: 132 ,
,
) (127410: 274 + 307200:: 480 - 907) 99.
Выполнив такое задание, учащиеся конечно будут спрашивать могут ли получаться такие большие числа. Можно попросить переправить примеры, а это значит, закрепление.
2. 5 класс, тема "Действия над десятичными дробями".
Каждому ученику выдается карточка с заданием.
Задание.
Найдите
значения буквенного выражения
a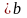 :
(c
+ d)
при
значениях букв, указанных в таблице.
Запишите полученные значения в строке
"результат" и закрасьте каждую
часть своего рисунка цветом, соответствующем
в данной таблице данному результату.
:
(c
+ d)
при
значениях букв, указанных в таблице.
Запишите полученные значения в строке
"результат" и закрасьте каждую
часть своего рисунка цветом, соответствующем
в данной таблице данному результату.
Таблица
Значения букв |
|||||
a b c d |
7,7 2,21 3,62 13,38 |
24,7 11,9 16,56 38,69 |
14,3 3,23 5,49 5,56 |
1,33 18,7 3,78 6,67 |
9,1 20,9 7,15 7,15 |
Результат |
|
|
|
|
|
Цвет на картинке |
красный |
желтый |
коричневый |
черный |
серый |
Например, в первом столбце таблицы ученик должен получить результат 1,001. На своей картинке он должен закрасить красным цветом те участки, где записано это число, то есть платьице.
Рисунок детям можно давать один и тот же, а сложность буквенного выражения можно варьировать. Если все ученики выполнят задание, то рисунок у всех будет раскрашен одинаково. Перед уроком рисунки вывешиваются на доске. Туда же учитель помещает и свой рисунок. По этому эталону дети мгновенно видят, кто ошибся и где именно. Обычно обсуждение работы начинается уже на перемене. Не дождавшись звонка на урок, дети делятся своими впечатлениями, обсуждают задание и вовлекают в этот разговор учителя.
3. 6 класс, тема "Координаты точки на плоскости".
Каждому ученику выдается карточка с набором координат. Отмечая точки, по их координатами соединяя их в порядке записи, ученики получают фигуру и заштриховывают её. А эта фигура оказывается на что похожа? Правда интересно?!
Карточка № 1.
А (-5;1); В (-3;1); С (-2;3); D (0;4); E (2;3); G (3;1); F (3;1); K (2; - 2);
M (2; - 4); N (0; - 4); T (0; - 3); P (-2; - 3); H (-3; - 2); L (-1; - 1); S (-3; - 1); R (-3; 0).
4.5 класс, тема "Действия с дробями".
"Положите" в каждый мешок по два числа, сумма которых равна единице.
Любое задание творческого характера призвано развитию совершенствованию логического мышления.
Следующую группу составляют задания на обучение классификации, анализу отношений, сравнений.
.5 класс, тема "Натуральные числа и шкалы".
Анализ отношений.
В каждом задании напечатаны пять слов. Под этим списком должны стоять еще четыре слова, разбитые на две пары. Из этих четырех слов даны только три. Выберите из списка одно слово, которое нужно поставит вместо знака вопроса, чтобы найденное четвертое слово находилось с третьим в таком же отношении, что и первое со вторым.
. Величина, количество, цифра, счет, номер.
Слово - буква.
Натуральное число - ?
(цифра)
. Числа, девять, символы, десять, бесконечное множество.
Алфавит - тридцать три.
Цифры - ?
(десять)
. Температура, масса, цифра, количество предметов, величина.
Слово - суть.
Натуральное число - ?
(количество предметов)
. Разность, умножение, произведение, деление, частное.
Слагаемое - сумма.
Множитель - ?
(произведение)
. Минуты, секунды, время, стрелки, цифры.
Термометр - температура.
Циферблат - ?
(время)
. Шкала, сантиметр, прямая, длина, деления.
Весы - масса.
Линейка - ?
(длина)
. Координата, начало, единичный отрезок, направление, шкала.
Мороженое - порция.
Координатный луч - ?
(единичный отрезок)
Классификация.
. Даны числа: 12, 0, 15, 1, 8, 5, 2, 3, 44.
Распределите их по следующим признакам:
Однозначные числа
Двузначные числа
Натуральные числа в порядке возрастания
Целые числа
Цифры
. В каждом из четырех данных ниже списков подчеркните лишнее слово.
Отрезок, прямая, луч, треугольник, фигура, квадрат. (фигура)
Сантиметр, миллиметр, дециметр, длина, метр. (длина)
Тонна, центнер, масса, грамм, пуд. (масса)
Треугольник, прямоугольник, многоугольник, квадрат, пятиугольник.
(многоугольник)
Развитие навыков сравнения.
Укажите в таблице как можно больше общих свойств понятий "отрезок", "луч", "прямая" и как можно больше различий.
Общие свойства |
Различия |
||
|
отрезок |
луч |
прямая |
|
|
|
|
Некоторые виды заданий, которые могут быть использованы в качестве домашних заданий творческого характера.
Кросснамберы - один из видов числовых ребусов. В переводе с английского слово "кросснамбер" означает "кресточислица". При составлении кросснамберов применяется тот же принцип, что и при составлении кроссвордов: в каждую клетку вписывается один знак, "работающий" на горизонталь и вертикаль. В каждую клетку кресточислицы вписывается по одной цифре. А чтобы не было путаницы, номера заданий обозначаются буквами. Числа, подлежащие отгадыванию, - только целые положительные; запись таких не может начинаться с нуля (то есть 42 нельзя записать 042). Следует отметить, что не всякий крссснамбер допускает только один ответ. Иногда намеренно задаются такие вопросы, на которые нельзя ответить однозначно. Более того, можно указать в качестве ответа не два или три, а бесконечно много чисел. Такая неопределенность подстегивает интерес к заданию. А из затруднения всегда можно выйти, если соотнести данное задание с тем, которое с ним пересекается [31].
Кроссворды - переплетение слов (крестословица). Чтобы разгадать кроссворд, надо слова, значения которых указаны в условии, записать по одной букве, начиная с пронумерованной клетки и заканчивая последней пустой, отдельно по вертикали и отдельно по горизонтали [33].
Чайнворд - термин "чайнворд" можно перевести с английского как "цепочка слов". Эта цепочка разгадывается "по лабиринту" следующим образом: слово, значение которого указано в условии, записывается по одной букве в каждую клетку, начиная с пронумерованной и кончая клеткой с очередным номером. Каждая последняя буква предыдущего слова является одновременно и первой буквой последующего. В данном случае слова"закручиваются"вокруг серых прямоугольников точно так же, как реальная цепочка накручивается на руку. Поэтому слова записываются не только справа налево, но и слева направо, и снизу вверх, и сверху вниз буква за буквой. Требуется не только хорошее знание математических терминов, но и недюжинное внимание, и безукоризненная аккуратность, чтобы заполнить весь чайнворд [33].
Идея составления фигур из цепочки слов подсказывает хорошие творческие задания для учащихся: придумать чайнворды, которые предстанут в виде каких-то фигур, причем таких, чтобы у каждого ученика была "своя" фигура без повторений.
Криптограммы - это шифрованное письмо. Чтобы разгадать криптограмму, надо расшифровать ключевые слова, приведенные к ней. Количество букв в ключевом слове соответствует количеству чисел в нем. Одно и тоже число, встречающееся как в ключевых словах, так и в самой криптограмме, соответствует одной и той же букве. Следует отметить, что иногда не все буквы, встречающиеся в ключевых словах, используются при расшифровке криптограммы [33].
Символ (треугольник, круги тому подобное) между числами в криптограмме означает промежуток между словами в зашифрованном письме. Заменив все числа криптограммы соответствующими им буквами, получаем её расшифровку.
Ключ к разгадыванию криптограмм содержит ответы на математические вопросы, поэтому расшифровка - полезное занятие. В результате кропотливой работы постепенно складывается мудрое изречение, которое очень интересно домысливать, пока оно еще не полностью составлено, чтобы затем проверить свою догадку, прочитав фразу до конца.
Математические загадки (головоломки) - некоторые рассчитаны на применение обычных правил сложения, вычитания, умножения и деления, а для иных понадобиться более абстрактные математические понятия, операции и размышления. Это магические квадраты, волшебные сечения, мозаичные головоломки, задачи на топологии и другие. Головоломки различаются по сложности, но все они математически строги к тому же требуют нестандартного подхода [23].
Творческий характер носят задания моделирование различных макетов. Например, при изучении в 6 классе темы "Координаты на прямой", учащимся предлагается дома изготовить модель координатной прямой, которая будет активно использоваться на протяжении изучения всей темы "Положительные и отрицательные числа". Также при изучении темы "Прямоугольный параллелепипед" домашним заданием может служить изготовление макета параллелепипеда, успевающие учащиеся должны сами изготовить его развертку, а слабым учащимся она может быть предоставлена учителем. В старших классах учащиеся выполняют макеты более сложных объемных фигур.
Домашним заданием творческого характера также может служить изготовление наглядных методических пособий, плакатов имеющих методическую ценность.
Например, к обобщающему уроку по теме "Тригонометрические уравнения" учащимся предлагается классифицировать все известные методы решения тригонометрических уравнений и оформить это в виде плаката или еще каким-либо образом.
И нельзя упомянуть о том, что творчество учащегося, несомненно, проявляется и при решении математических задач - главное чтобы эта задача была нестандартной.
Для формирования самостоятельности мышления, воспитания творческой активности необходимо включать нестандартные задачи в систему домашних упражнений.
Нестандартные задачи - это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Однако любая задача, считающаяся стандартной, в тот момент, когда ученик с ней сталкивается впервые, является для него нестандартной. После того, как нестандартная задача решена, любая аналогичная задача становится стандартной.
Таким образом, нестандартная задача ─ это задача, алгоритм решения которой учащимся неизвестен, т.е. учащиеся не знают заранее ни способов её решения, ни того, на какой учебный материал опирается решение.
Как учитель может помочь учащимся решать нестандартные задачи? Универсального метода, позволяющего решить любую нестандартную задачу, нет, т.к. нестандартные задачи в какой-то степени неповторимы.
Рассмотрим отдельные методические приемы обучения учащихся решать нестандартные задачи:
. Прежде всего, надо отметить, что научить учащихся решать задачи (в т. ч. нестандартные) можно только в том случае, если у учащихся будет желание их решать, т.е. если задачи будут содержательными и интересными с точки зрения ученика. Поэтому задача учителя - вызвать у учащихся интерес к решению той или иной задачи. Необходимо тщательно отбирать интересные задачи и делать их привлекательными для учащихся. Это могут быть - задачи-шутки, задачи-сказки, старинные задачи и т.п. Одно бесспорно: наибольший интерес у школьников вызывают задачи, взятые из окружающей жизни, задачи, связанные со знакомыми вещами, опытом. Важно показать детям, что от решения математической задачи можно получить такое же удовольствие, как от разгаданного кроссворда или ребуса.
. Задачи не должны быть слишком легкими, но и не слишком трудными, т.к. ученики, не решив задачу или не разобравшись в решении, предложенном учителем, могут потерять веру в свои силы. В этом случае очень важно соблюсти меру помощи. Прежде всего, учитель не должен знакомить учащихся с уже готовым решением. Подсказка должна быть минимальной.
Рассмотрим примеры решения нестандартных задач.
Задание №1.
Прохожий заметил идущий на остановку автобус в 180 метрах позади себя. Чтобы не опоздать, он побежал и через 12 секунд прибежал на остановку одновременно с автобусом. С какой скоростью пришлось бежать прохожему, если известно, что автобус движется со скоростью 19 м/сек?
Прежде чем давать эту задачу на дом, целесообразно прочитать ее в классе и сделать к ней рисунок, т.е. составить графическую модель ситуации, описанной в задаче:

I способ.
) 19 12 = 228 (м) - расстояние, которое проехал автобус;
) 228 - 180 = 48 (м) - расстояние, которое пробежал прохожий;
) 48: 12 = 4 (м/с) - скорость прохожего.
Ответ: 4 м/с.
II способ.
) 180: 12 =15 (м/с) - скорость, с которой автобус догоняет прохожего;
) 19 - 15 = 4 (м/с) - скорость прохожего.
Ответ: 4 м/с.
Наводящие вопросы, которые могут быть заданы классу:
На какую из ранее решенных задач похожа эта задача?
I способ.
) Какую величину требуется найти в задаче? (скорость)
) Какие величины надо знать, чтобы определить скорость движения? (путь и время)
) Какие из них нам известны? (время)
) Подумайте, как определить путь.
II способ.
) О каком движении речь идет в задаче: навстречу, вдогонку, объекты сближаются или удаляются? Как бы вы охарактеризовали скорость, с которой меняется взаимное расположение объектов? (движение вдогонку, автобус догоняет пешехода, скорость сближения)
) В этой задаче двигаются автобус и прохожий, причем автобус догоняет прохожего. Какие скорости и расстояния рассматриваются, когда речь идет о движении вдогонку? (скорости движущихся объектов, скорость сближения или удаления, расстояние между объектами, время, которое требуется, чтобы одному из них догнать другого).
) Какие из этих величин известны, какие нет? Какая из них искомая? (известно время, которое потребовалось автобусу, чтобы догнать прохожего, скорость автобуса; неизвестна скорость сближения; искомая величина - скорость прохожего).
) Как определить неизвестные величины?
Здесь второе решение короче, но додуматься до него труднее. Поэтому не следует торопиться с тем, чтобы дать детям готовое решение, эффект будет минимальный. Лучше к этой задаче возвращаться в течение нескольких уроков, давая детям возможность все глубже осознавать описанную в ней ситуацию.
отрезка
ML,
1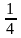 длины отрезка MK,
1
длины отрезка MK,
1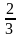 длины отрезка NL.
длины отрезка NL.
Задание №2.
Пассажир поезда, идущего со скоростью 50 км/ч, заметил, что встречный поезд шел мимо него в течение 10 секунд. Определите длину встречного поезда, если его скорость - 58 км/ч.
Какие величины в задаче известны? Сделаем рисунок:
Длина поезда - это расстояние от начала головного вагона до конца хвостового вагона. Какие величины мы обычно используем, чтобы найти расстояние?
Как бы вы решали задачу, если бы поезд, в котором сидел пассажир, стоял на месте?
Решение.
) 50 + 58 = 108 км/ч скорость, с которой встречный поезд проехал мимо пассажира.
) 108 (км/ч) = (108 1000): 3600 (м/с) = 30 (м/с).
) 30 10 = 300 (м) - длина поезда.
Ответ: 300 м.
Задание №3.
а). От пристани А вниз по течению реки отправился катер. В это же время от пристани В навстречу ему вышел второй катер с такой же собственной скоростью. Первый катер достиг пристани В через 4 ч. На каком расстоянии от пристани А был в это время второй, если скорость течения 2 км/ч?
б) В случае затруднений, постарайтесь определить, на сколько первый катер проходит больше километров за 1 час, чем второй
в) Если вы так и не смогли решить задачу, постарайтесь разобраться в том, как это можно сделать, из следующего текста.
Первый катер при движении по течению за 4 ч "выиграл" 8 км (4 2) по сравнению с тем расстоянием, которое он прошел бы за это время, двигаясь в стоячей воде, а второй катер столько же километров "проиграл", так как двигался против течения. Всего же второй катер за 4 ч "проиграл" первому 16 км. Значит, на таком расстоянии он был от A тогда, когда первый прибыл в B.
Подсказки и решение этой задачи следуют сразу после условия, под буквами б) и в).
Задание №4.
На отдельном листе бумаги, используя чашку вместо циркуля, проведите карандашом окружность. Вырежьте получившийся круг и подумайте, как при помощи перегибания найти его центр. Подумайте, как найти центр круга в случае, если круг перегнуть нельзя.
Выполнение первого задания - найти центр вырезанного круга перегибанием, как правило, затруднений не вызывает.
Если же круг перегнуть нельзя, то центр найти сложнее. Здесь учащимся следует предложить подумать, какие из свойств углов и окружностей, с которыми они познакомились, можно использовать в этой задаче. Оказывается, достаточно построить прямой угол BAC, где точки A, B, C принадлежат окружности, тогда BC - диаметр, а его середина - центр окружности.
Мы рекомендуем учителю обязательно рассмотреть эти задачи с учащимися, так как в 6 классе им будут предложены задания такого типа: на рисунке изображена окружность, центр которой не отмечен, и требуется определить длину этой окружности, измерив ее диаметр или радиус.
Если учащиеся не знакомы с тем, как определить диаметр или радиус окружности, центр которой не известен, выполнить такое задание им будет нелегко.
Задание №5.
Катер, встретив плот, продолжал движение еще в течение получаса в том же направлении, а затем развернулся и направился обратно. Сколько ему понадобится времени, чтобы догнать плот?
Эта задача вызывает затруднения даже у учащихся старших классов. Но, поскольку они знакомы с преобразованием буквенных выражений, в большинстве случаев им удается получить правильный ответ.
Как правило, пятиклассники либо приносят решение в буквенной форме, которое сделали родители, либо высказывают некоторые предположения, с обоснованием которых у них возникают затруднения, либо задают какие-нибудь значения скоростей катера и течения и решают задачу с числовыми данными.
Последний вариант наиболее приемлем. Следует предложить учащимся задать различные значения для скоростей катера и течения и решить задачу с этими данными. Во всех случаях получается один и тот же результат. После этого учащиеся высказывают предположение, что результат не зависит от числовых данных. Учитель предлагает подумать - почему?
Обоснования могут быть различными по форме. Приведем одно их них.
Скорость удаления катера от плота (движение против течения):
(vсобст. катера - vтечения) + vплота (течения) = vсобст. катера.
Скорость сближения катера и плота (движение по течению):
(vсобст. катера + vтечения) - vплота (течения) = vсобст. катера.
Творческие задания должны являться неотъемлемой частью домашнего задания по математике, они формируют самостоятельность мышления, воспитывают творчески активную личность.
