
- •Содержание
- •Глава 1. Домашнее задание - важнейшее звено процесса обучения, воспитания и развития личности школьника §1. Роль домашнего задания в развитии личности учащегося
- •§2. Домашнее задание - необходимая часть процесса обучения
- •§3. Виды домашних заданий
- •Глава 2. Пути повышения эффективности домашней работы учащихся
- •§1. Методика конструирования, постановки и контроля домашнего задания при обучении математике
- •§2. Взаимосвязь домашнего задания с изучением нового материала
- •§3. Дифференцированный подход при организации домашней работы
- •§4. Домашние задания творческого характера
- •§5. Повышение интереса учащихся к математике через домашние задания занимательного характера
- •Заключение
- •Список литературы
§2. Взаимосвязь домашнего задания с изучением нового материала
Повышение качества знаний учащихся во многом определяется тем, как поставлена их домашняя работа. В книге И.Ф. Харламова "Как активизировать учение школьников" горится, что задача повышения эффективности обучения и интенсификации учебного труда школьников может быть успешно решена только при условии, если высокое качество урочных занятий будет подкрепляться и разумно сочетаться с хорошо организованной домашней работой. И с этим нельзя не согласится [30]. Однако на практике руководство домашним заданием чаще всего сводится либо к проверке самого факта выполнения домашнего задания, либо к выяснению затруднений, с которыми учащиеся столкнулись при выполнении домашнего задания, либо к фронтальной проверке хода решения задач или только ответов. Иногда задания частично или полностью воспроизводятся на доске. А бывает и так, что домашнее задание на уроке не фигурирует совсем, хотя известно, что если результат домашней работы учащихся систематически не используется на уроке, не подвергается поощрению и оценке, то это приводит к потере интереса к выполнению домашнего задания. Нередки случаи, когда группы учащихся приходят на урок с невыполненным заданием. Это, несомненно, связано с малой эффективностью работы в направлении усиления роли домашнего задания на уроке.
В школьной практике сложилось так, что задания, отбираемые для работы дома, в основном несут функции закрепления того, что разъяснялось в классе. Тем самым их обучающая роль на последующем уроке оказывается ограниченной. Каким образом привлечь учащихся к домашнему заданию на уроке? Как показать его значимость? Более глубокое изучение рассматриваемого вопроса показало необходимость изменить содержание и подбор домашнего задания, заставить домашнее задание "работать" на уроке, продумать возможность использования его результатов в дальнейшем ходе урока.
Достижение основной цели урока существенно зависит от того, в какой мере учащиеся подготовлены к успешному восприятию нового материала. Эта учебная задача решается на этапе проверки домашнего задания и повторения. Предполагается, что задание, данное учащимся на прошлом уроке, в какой-то мере учитывает отмеченную необходимость. На самом уроке проверяется и воспроизводится в первую очередь тот учебный материал, который непосредственно необходим для успешного восприятия нового.
При рассмотрении видов домашних заданий уже упоминалось о домашних заданиях, которые подготавливают учащихся к восприятию нового материала. Также упоминалось, что эффективность домашнего задания зависит от перспективы дальнейшего использования результатов домашней работы учащихся, от того, насколько активно они используются при получении новых знаний. Чаще всего учитель предлагает учащимся домашнее задание с целью закрепления того материала, который изучался на уроке. Но как показал опыт, важно продумать содержание этого задания и с позиции возможности дальнейшей работы с ним в классе.
Изучение вопроса подбора домашних заданий по математике показало, что возможности их использования на уроке в различных учебных целях довольно значительны. Необходимо, чтобы домашнее задание получало на следующем уроке дальнейшее развитие.
. Использование домашнего задания может выражаться в том, что вместе с его проверкой учитель осуществляет углубленное повторение ранее изученного материала, то есть закрепление того, что разъяснялось в классе. Например, для закрепления формулы площади трапеции можно предложит решить дома следующую задачу: "Вычислите площадь трапеции, основания которой 12 см и 16 см, а высота 15см".
Правильность решения этой задачи целесообразно проверить воспроизведением его на доске.

Рис.1
Однако планируя повторение и углубление знаний учащихся, полезно предложить всему классу решить на её основе две другие задачи:
) Какое основание должен иметь параллелограмм, равновеликий данной трапеции и имеющий те же высоту?
Обозначив
основание параллелограмма и его площадь
соответственно через a
и
S,
учащиеся решают эту задачу так: S
= S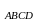 ,
а
,
а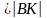 = 210, а
= 210, а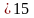 = 210, а
=
210: 15 = 14 (см). Получилось, что основание
параллелограмма равно средней линии
трапеции.
= 210, а
=
210: 15 = 14 (см). Получилось, что основание
параллелограмма равно средней линии
трапеции.
) Используя чертеж трапеции (рис.1), постройте параллелограмм, равновеликий ей, с той же высотой.

Рис.2
Если урок целиком посвящается повторению и углублению знаний учащихся, то можно предложить еще две задачи в аналогичной постановке.
) Вычислите длину основания треугольника, равновеликого данной трапеции и имеющего с ней одинаковую высоту.
4) Дана трапеция. Используя её чертеж, постройте треугольник, равновеликий ей, с той же высотой.

Рис.3
Решение задачи 3) учащиеся могут оформить так же, как и задачи 1). Ответ к задаче 4) дан на рисунке 3.
Из приведенного примера видно, что проверяемое в классе домашнее задание используется для повторения понятия равновеликости плоских фигур, формул площади параллелограмма и треугольника. Кроме того, вычислительная задача подкрепляется возможностью конструирования равновеликих фигур, отвечающих некоторым условиям решенных задач на вычисление.
Таким образом, повторение и углубление знаний органически соединяются с домашним заданием, но проводятся более рационально, чем, если бы предложенные на уроке задачи ставились вне связи с ним. Здесь используются выполненный дома чертеж, данные задачи и результаты её решения. Работа по домашней задаче как бы продолжается в классе, только на более высоком уровне проводимых рассуждений.
Приведу еще пример аналогичной постановки работы. Допустим, в качестве домашнего задания была задана следующая задача6 "Постройте графики функций, заданных формулами:
а) f
(x)
= x
;
б) f
(x)
=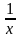 ".
".
На следующем уроке можно изобразить графики этих функций на доске (рис.4), а затем работу с ними продолжить.
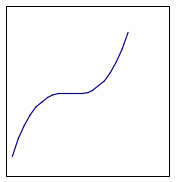
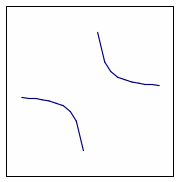
Рис.4
Учитель предлагает учащимся выяснить, как можно использовать построенные дома графики, чтобы получить графики функций
f
(x)
=
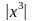 и f
(x)
=
и f
(x)
=
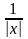 .
.
В результате коллективного обсуждения учащиеся подводятся к мысли, что для построения графиков новых функций лучше изменить форму записи их задания. На основании определения модуля получим следующее:
f
(x)
=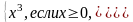
f
(x)
=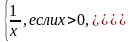
Теперь, используя графики функций из домашнего задания, учащиеся строят графики функций f (x) = и f (x) = : на множестве положительных чисел (для первого графика - на множестве неотрицательных чисел) значения функций f (x) = и f (x) = совпадают соответственно со значениями функций f (x) = x и f (x) = , на множестве отрицательных чисел их значения противоположны. Следовательно, на множестве отрицательных чисел графики функций f (x) = и f (x) = будут симметричны соответственно графикам f (x) = x и f (x) = относительно оси абсцисс, на множестве положительных чисел их графики совпадут. В этих же системах координат другим цветом строятся графики новых функций (рис.5).
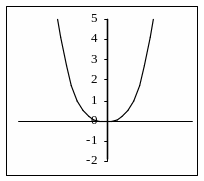
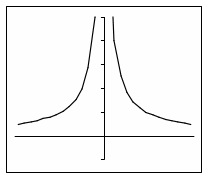
Рис.5
Рассмотренный пример показывает целесообразность использования домашнего задания в предложенном направлении. Во - первых, в связи с постановкой новых задач на основе домашних повторяется одно из трудных для учащихся понятий - модуль числа. Во - вторых, графики функций f (x) = и f (x) = легко получить из графиков функций f (x) = x и f (x) = .
2. Домашнее задание можно использовать в тех случаях, когда необходимо создать на уроке проблемную ситуацию.
Так, после определения параллельности прямой и плоскости и доказательства теоремы существования этого отношения (признака параллельности прямой и плоскости) для закрепления изученного на уроке учащимся предлагается решить задачу: "Известно, что прямая параллельна плоскости. 1) Параллельна ли она любой прямой, лежащей в этой плоскости? 2) Может ли она пересечь хотя бы одну из таких прямых?"
Остановимся только на случае, когда прямая не лежит в данной плоскости. Ответить на второй вопрос задачи учащиеся смогут довольно легко, так как из допущения того, что прямая может пересечь хотя бы одну прямую, лежащую в плоскости, с необходимостью последует, что она пересечет и саму плоскость. Это противоречит данному условию. Правильно ответить на первый вопрос помогут наглядные представления, которые легко можно создать, моделируя взаимное расположение прямой и параллельной ей плоскости. Такие представления приведут учащихся к выводу, что прямая, параллельная плоскости, не может быть параллельна любой прямой, лежащей в плоскости.
Используя
этот вывод учащихся, учитель в порядке
развития задания может поставить
следующий вопрос: "Существует
ли в плоскости хотя бы одна прямая,
параллельная данной?" Наглядное
рассмотрение факта опять-таки может
натолкнуть их на правильную мысль о
существовании такой прямой. Учитель,
естественно, говорит о том, что опытное
обнаружение факта в математике не
является доказательством. В данном
случае, если допустить, что прямая,
параллельная данной, существует (случай,
когда данная прямая не лежит в плоскости),
то как можно было бы её провести?
Обсуждение приводит учащихся к тому,
что сделать это можно так: взять в
плоскости
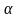 произвольную точку А, провести плоскость
произвольную точку А, провести плоскость
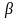 через точку А и прямую b;
эта плоскость пересечет плоскость
по прямой с, проходящей через точку А.
"Будут
ли в этом случае с
через точку А и прямую b;
эта плоскость пересечет плоскость
по прямой с, проходящей через точку А.
"Будут
ли в этом случае с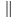 b?"
Этот
факт нетрудно доказать. Прямые с и b
(рис.6) лежат в одной плоскости
и не пересекаются, так как в противном
случае прямая b
пересекалась бы с плоскостью
,
чего быть не может. Следовательно, с
b.
b?"
Этот
факт нетрудно доказать. Прямые с и b
(рис.6) лежат в одной плоскости
и не пересекаются, так как в противном
случае прямая b
пересекалась бы с плоскостью
,
чего быть не может. Следовательно, с
b.
Таким образом, проверяя в классе решение домашней задачи, учитель ставит перед учащимися ряд последовательных задач-проблем, связанных с ней. Решив их, учащиеся не только убедятся в существовании в плоскости прямой, параллельной данной прямой, но тем самым установят новое соотношение между прямыми и плоскостями: " Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой".

Рис.6
Изучение этой теоремы и являлось целью данного урока, но цель была достигнута на основе домашнего задания, позволяющего поставить и разрешить последовательно несколько проблемных задач.
Приведенный пример иллюстрирует прием использования домашнего задания для создания проблемной ситуации и постановки проблемы, что более рационально, чем, если бы учитель начинал изложение материала на уроке (пусть и в проблемном плане): подготовка мышления учащихся к осознанию необходимости нового знания частично проходила при выполнении домашнего задания. В классе же учитель более четко раскрыл перед учащимися суть проблемы и целенаправленно подвел их к её решению.
. Домашнее задание можно дать и таким образом, чтобы изложение нового материала являлось его обобщением.
Так, перед тем как на уроке ввести понятие среднего пропорционального и теоремы, утверждающей его существование, целесообразно в качестве домашнего задания дать задачу: "Из вершины прямого угла данного треугольника проведена высота. Сколько пар подобных треугольников образовалось на чертеже?", добавив к ней еще одно задание: "Из соответственных сторон каждой пары подобных треугольников составьте три равных отношения".
Проверяя на следующем уроке выполнение домашнего задания, учитель по предложению учеников делает такие записи (рис.7):

Рис.7
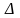 ADC
~
ACB,
ADC
~
ACB,
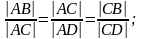
ACD
~
CDB,

CDB
~
АCB,
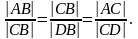
Затем учитель выясняет у учащихся, не заметили они какую-либо особенность в пропорциях, состоящих из двух первых отношений. Обнаруживается, что в этих пропорциях средние члены повторяются. Таким образом, решение домашней задачи, которая была задана с целью углубления знаний о подобных треугольниках, привело учащихся к понятию отрезков, средних пропорциональных между двумя другими. Учителю остается лишь сформулировать определение таких отрезков и подтвердить по пропорциям, что такие отрезки существуют.
Итак, обобщая домашнее задание, учителю удается ввести понятие среднего пропорционального и констатировать его существование. Ясно, что такой методический прием более оправдан, чем если бы новый материал излагался вне связи с домашним заданием. Здесь же многое из того, что необходимо объяснить на уроке, уже продумано учащимися дома; на уроке происходит лишь обобщение. Налицо более глубокое понимание нового материала и значительная экономия времени на его изложение.
Готовясь
к изучению темы "Графический способ
решения уравнений с одной переменной",
можно в качестве домашнего задания
предложить учащимся построить в одной
и той же системе координат графики
функций, заданных формулами у =
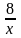 и у = х
,
а в другой - графики функций, заданных
формулами у =
и у = х
,
а в другой - графики функций, заданных
формулами у =
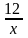 и у = х +1. Задание предназначено для
повторения материала о графиках различных
функций, но учитель заранее предусматривает
возможность построить на нем изложение
нового материала. С этой целью он
предлагает учащимся пары графиков
построить в одной и той же системе
координат.
и у = х +1. Задание предназначено для
повторения материала о графиках различных
функций, но учитель заранее предусматривает
возможность построить на нем изложение
нового материала. С этой целью он
предлагает учащимся пары графиков
построить в одной и той же системе
координат.
На следующем уроке выполненное задание целесообразно проверить по заранее заготовленным рисункам (рис.8,9).
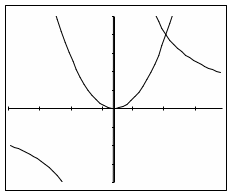
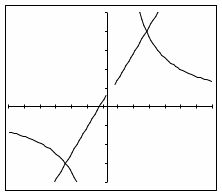
Рис.8 Рис.9
Далее учитель может повести коллективную беседу по следующим вопросам:
) При каких значениях х функции у = и у = х принимают равные значения?
(ответ: при х = 2).
) Что можно сказать о значениях выражений и х при х = 2?
(ответ: при х = 2 значения этих выражений равны).
Ответ на второй вопрос означает, что х = 2 является корнем уравнения = х . Делается вывод, что, построив графики данных функций в одной системе координат и найдя абсциссу точки их пересечения, получаем графическое решение уравнения.
Рассмотрение выполнения второго задания явится иллюстрацией того, как графическим способ можно решить уравнение = х +1.
Проверка выполнения домашнего задания в этом случае разумно сочетается с новым истолкованием его содержания. Если бы дома учащиеся не построили графики заданных функций, то изложение нового материала значительно затянулось бы. В то же время данные к уроку упражнения по содержанию являются вполне правомерными; такого рода упражнения содержатся в предыдущих разделах повторительного характера, только их полезнее задавать именно к этому уроку, чтобы, направив обобщение на изложение темы урока, более рационально и глубоко рассмотреть новый материал.
Приведем еще несколько примеров домашних заданий, обобщение содержания, которого является изложением нового материала.
Перед темой "Формулы сокращенного умножения" изучается тема "Умножение многочлена на многочлен".
На последнем уроке изучения этой темы, то есть накануне перехода к формулам сокращенного умножения, учащимся на дом наряду с другими даются задания:
"Выполните умножение:
) (а
+ в)
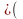 а
+ в);
а
+ в);
) (а - в) а - в);
) (2т + 3) 2т+3);
) (4 - 6х) 4 - 6х).
В ходе урока на этапе проверки домашнего задания эти упражнения проверяются последними.
После проверки учитель обращает внимание учащихся на то, что во всех равенствах в левой части по сути стоят квадраты двучленов, поэтому слева можно дописать соответствующие выражения.
Вид доски во время проверки домашнего задания: № 1) (а + в) а + в) = а + ав +ва + в = а + 2 ав + в
№ 2) (а - в) а - в) = а - ав - ва + в = а - 2 ав + в
№ 3) (2т + 3) 2т+ 3) = 4т + 6т + 6т + 9 = 4т + 12т + 9
№ 4)
(4 - 6х)
|
После обсуждения стираем номера упражнений и дописываем слева квадраты двучленов:
(а + в) = (а + в) а + в) = а + ав +ва + в = а + 2 ав + в
(а - в) = (а - в) а - в) = а - ав - ва + в = а - 2 ав + в
Далее подчеркиваем начальное и конечное выражение в первых двух равенствах и выписываем соответствующие равенства на левой (откидной) части доски, оставив место для заголовка:
(а + в) = а + 2 ав + в
(а - в) = а - 2 ав + в
На предыдущих уроках на этапе устных упражнений учащимся предлагались задания на чтение выражений. Сейчас им предлагается прочитать полученные равенства. Учитель открывает перед учащимися суть этих формул: "Эти равенства позволяют, не выполняя умножения, сразу находить квадрат суммы или разности выражений. Поэтому они получили название "Формулы сокращенного умножения". Это тема сегодняшнего урока. Запишите её в тетрадь и запишите эти две формулы". Учитель записывает тему на доске над формулами.
Переходим к последним двум заданиям. Здесь тоже даны квадраты двучленов. Давайте подумаем, как можно было бы преобразовать эти выражения, используя равенства, которые мы только что записали.
(2т
+ 3)
= (2т)
+
2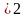 т
т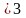 +
3
= 4т
+
12т + 9
+
3
= 4т
+
12т + 9
Учитель предлагает сравнить результат с тем, что получен дома.
Аналогичные рассуждения проводятся и с последним домашним выражением.
(4
- 6х)
= 4
- 2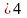
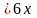 +
(6х)
=
16 - 48х + 36х
.
+
(6х)
=
16 - 48х + 36х
.
Далее следует работа по формированию умений применения изученных формул.
При переходе к следующим формулам учащимся соответственно даются на дом такие задания:
) (а - в) а + в);
(5 - т) 5 + т);
(2х + 7) 2х - 7).
) (а - в) а +ав + в );
(х - 3) х +3х + 9);
(а + в) а - ав + в );
(2 + у) 4 - 2у + у ).
Результаты, полученные в ходе выполнения этой работы, также могут быть использованы в дальнейшем ходе урока.
К уроку алгебры, на котором планируется изложение материала о зависимости положения графика функции у = kх + b от значений k и b, целесообразно в качестве домашнего задания предложить следующее задание: построить в одной системе координат графики уравнений у = 3х +2, у = 3х - 2, у = 3х, а в другой - графики уравнений у = х + 2, у = 3х +2, у = - 2х + 2.
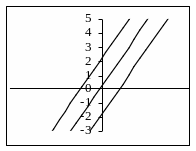
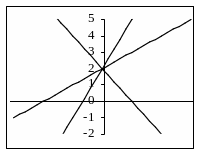
На следующем уроке домашнее задание воспроизводится на доске. Внимание учащихся обращается на особенности расположения графиков этих функций. В одной системе координат все прямые параллельные, а в другой - пересекаются в точке (0;
). Учитель ставит перед учащимися вопрос: " Какую особенность имеют данные уравнения?" Учащиеся должны проанализировать вид уравнений и выяснить зависимости положения графиков от k и b, а это и является содержанием нового материала. На основе выполненного дома упражнения учащиеся выполняют обобщение наблюдаемого явления, чем и открывают для себя новый теоретический факт.
. Можно разработать такие домашние задания, что изучение нового материала на уроке будет проходить в постоянном обращении к домашнему заданию. Например, по алгебре в VIII классе на дом были заданы упражнения на решение квадратных уравнений выделением квадрата двучлена; тема следующего урока - решение квадратных уравнений по формуле корней. При закреплении полученных на уроке знаний целесообразно решить те же квадратные уравнения, что были заданы на дом, но уже по формуле, проверяя тем самым правильность решения домашнего задания.
х |
0 |
|
|
|
у |
|
|
|
|
При изучении темы "Функция у = kх , её свойства и график" на второй урок по данной тема учащимся можно предложить следующее задание на дом: "1) Заполните таблицу, если у = 2х .
) Отметьте на координатной плоскости точки с координатами из заполненной вами таблицы.3) Отметьте точки, симметричные построенным относительно оси ординат и проверьте, удовлетворяют ли их координаты уравнению у = 2х ".
На следующем уроке перед учащимися целесообразно поставить следующие вопросы при этом домашнее задание необходимо воспроизвести на доске:
) Можно ли утверждать, что все построенные вами точки принадлежат графику функции у = 2х ? Ответ обоснуйте.
)
Добавьте ещё какие-нибудь точки и
постройте график функции у = 2х
(например, точки (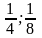 ),
(
),
(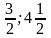 )).
)).
) Как бы вы назвали этот график? Похож ли он на знакомый вам график? (Похож на параболу).
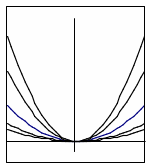
) Сравните полученный график с графиком функции у = х . Что произошло? (Ветви сблизились). В случае затруднений при ответе, можно штриховой линией построить график функции у = х в той же системе координат, что и график функции у = 2х .
) А как будут выглядеть графики функций у = 3х и у = 4х ? (парабола будет еще ближе расположена к оси ординат, ветви будут еще круче).
) А
если будем уменьшать коэффициенты при
х
:
у =
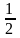 х
;
у =
х
?
Целесообразно будет предложить учащимся
построить графики данных функций в той
же системе координат, но обязательно
другим цветом. В одной системе координат
получаются параболы двух цветов, ветви
одних парабол ближе расположены к оси
ординат, ветви других наоборот
"расширяются". Естественно, учитель
должен заинтересовать учащихся таким
расположением графиков, поставив перед
ними вопросы: "Почему так получилось?
Какую особенность имеют данные уравнения?"
х
;
у =
х
?
Целесообразно будет предложить учащимся
построить графики данных функций в той
же системе координат, но обязательно
другим цветом. В одной системе координат
получаются параболы двух цветов, ветви
одних парабол ближе расположены к оси
ординат, ветви других наоборот
"расширяются". Естественно, учитель
должен заинтересовать учащихся таким
расположением графиков, поставив перед
ними вопросы: "Почему так получилось?
Какую особенность имеют данные уравнения?"
Внимание учащихся привлекается к анализу самих уравнений и выяснению зависимости вида параболы от коэффициента k, а это и является содержанием нового материла. Итогом проделанной работы может служить демонстрация пленок для графпроектора или слайдов, по которым еще раз обсуждаются свойства графика функции у = kх при k>0.
После
закрепления изученных свойств при
построении графиков, на дом учащиеся
получают задание аналогичное предыдущему,
только для функции у = - 2х
и сравнить полученный график с графиком
у = 2х
.
На следующем уроке этот материал
используется для изучения свойств
функции у = kх
при
всех k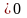 .
.
При
переходе к изучению темы "Функция у
=
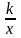 "
могут быть на дом заданы аналогичные
упражнения с заданием типа: (учащиеся
уже умеют строить график функции у =
"
могут быть на дом заданы аналогичные
упражнения с заданием типа: (учащиеся
уже умеют строить график функции у =
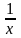 )
)
1) Построить точки, симметричные данным относительно: а) оси ординат; б) начала координат.
) Проверить, удовлетворяют ли координаты этих точек уравнению у = .
) Как, по вашему мнению, должен выглядеть график функции у = (при конкретных значениях k?
5. В методике преподавания математики слабо развиты домашние задания, предваряющие уроки обобщающего повторения. На таких уроках учитель обыкновенно решает с учащимися различные виды задач. При этом теоретический материал выступает в качестве обоснования решений, что, конечно, способствует его повторению, однако часто подбор домашних упражнений не приводит знания учащихся в систему. Возможности же разработки таких домашних заданий, которые приводили бы знания учащихся в более стройную систему, имеются. Так, готовясь к уроку обобщения по теме "Квадратные уравнения", полезно дать в качестве домашнего задания, например, такое: "Решите квадратное уравнение х - 2х - 3 = 0 не менее чем четырьмя способами". При выполнении этого задания учащиеся должны будут использовать все способы, которыми им приходилось решать квадратные уравнения, а именно:
) используя свойства корней квадратного уравнения;
) по формуле корней квадратного уравнения;
) графически;
) выделяя квадрат двучлена.
Решение квадратного уравнения многими способами приведет знания учащихся в систему, если на следующем уроке проверка правильности выполнения домашнего задания будет соединена с теоретическим обоснованием этих решений и выяснением того, в каких случаях наиболее удобно пользоваться тем или иным способом. Дальнейшая работа в этом плане должна пройти уже на других примерах.
Аналогичная постановка домашнего задания может иметь место при обобщении теоретического материала по теме "Площади многоугольников". Так, к уроку обобщающего повторения по указанной теме можно предложить такое задание: "Вывести формулу площади трапеции не менее чем тремя способами" [см. приложение].
Если на следующем уроке учитель сумеет организовать "защиту" этих решений учащихся, то домашняя работа может оказаться материалом для углубленного повторения и систематизации знаний, учащихся по названной теме.
Не часто в практике преподавания математики встречаются домашние задания, требующие установления взаимосвязи изученных понятий; постановка же их во многом способствует развитию мышления учащихся и вместе с там вызывает интерес к изучаемому материалу. Например, изучение темы "Четырехугольники" полезно было бы завершить уроком повторения, к которому можно предложить в качестве домашнего задания выполнить следующее: "Расположите понятия "параллелограмм", "квадрат", "прямоугольник", "ромб", "трапеция", "четырехугольник" в порядке соподчинения, то есть от более общих понятий к менее общим. Заполните схему".
Связь между указанными понятиями предопределяется данной учащимся схемой с незаполненными "клетками" (рис 10).
Рис.10
Задания в аналогичной постановке возможны и по многим другим темам школьной математики. Они заставляют учащихся задуматься над взаимосвязью понятий, а следующее за ними обсуждение способствует формированию системы знаний.
. Рассмотрим еще один тип задания, которое можно назвать "вопросы автору открытия". Например, при изучении в алгебре прямоугольной системы координат на плоскости ребятам предлагается дома подготовить вопросы автору открытия, которые помогли бы лучше и глубже понять его смысл или значение, а также особенности применения в практической деятельности. Отвечать на такие вопросы могут сами ученики, а если возникнут затруднения (вопрос окажется очень сложным или ответ на него не может быть однозначным), поможет учитель. Это задание по своей психологической сути тесно связано с серией заданий, в основе которых лежит подготовка к ролевым играм на уроках.
В предыдущем примере те учащиеся, которые получают установку представить себя автором, дома собирают разнообразную информацию, чтобы на следующем уроке быть готовым к ответу на неординарные вопросы, которые им могут задать одноклассники. Их ролевая установка - роль журналистов, которые берут интервью.
Можно предложить ученикам представить себя учителем и дома выбрать оптимальный, с их точки зрения, вариант объяснения того или иного материала, с точки зрения формы его подачи (через рисунок, схему, лабораторный метод, таблицу и т.п.) или с позиции особенностей индивидуального восприятия (собственно объяснения, доклад заранее подготовленного ученика, беседа, диспут).
Интересно проходит игра под названием "Докажи свою точку зрения", в которой есть две противоположные стороны: изобретатель - оппонент, они отстаивают свои взгляды. Изобретатель доказывает целесообразность и эффективность изобретения для внедрения в практику. Игра-диспут, конечно, проводится на уроке, но подготовка к ней ведется дома, в зависимости от роли, выбранной ребятами.
Если учитель посчитает необходимым, то он может по такому принципу организовать и коллективную дискуссию. Для этого класс разбивается на группы, каждая из которых будет отстаивать свою позицию, свой взгляд на проблему. Ученики к предстоящей дискуссии готовятся самостоятельно. Но можно предложить и другой вариант домашней подготовки. Школьники, объединившиеся в ту или иную группу, готовятся коллективно к предстоящей игре, заранее выбирая общую позицию, системы доказательств своей правоты. Для того чтобы подготовка такой группы была успешной, и все учащиеся работали в ней активно, состав её не должен превышать 5-6 человек. Кроме этого для проведения коллективной дискуссии от класса необходимо выдвинуть технического и научных экспертов, которые также должны специально готовиться: организационную и техническую часть (карточки, плакаты, таблицы) готовит технический эксперт, а научный готовится к серьезному анализу различных точек зрения на проблему, обсуждаемую в ходе дискуссии.
Такие задания, несомненно, носят творческий характер, и цель их будет достигнута лишь в том случае, если в классе будет создана особая психологическая атмосфера творческих исканий и коллективного труда. Одно из важнейших условий самой возможности успешного выполнения творческих заданий - особый тип общения учителя и ученика на уроке, который можно назвать диалогическим общением. Но диалогическим не в смысле постоянного обмена репликами между учителем и учеником, а в смысле равноправности заинтересованности собеседников во взглядах, мнениях друг друга.
В результате использования домашнего задания как средства подготовки к изучению нового материала успешно решаются следующие вопросы:
) в большей мере учащимися осознается необходимость выполнения домашнего задания;
) осуществляется в единстве проверка выполнения домашнего задания, его развитие и включение в изучение нового материала;
) экономится время на изучение нового материала;
) углубляются и систематизируются знания учащихся.
