10.Понятие отношений на множествах и способы их задания.

Когда говорят о родстве двух человек, Маша и Саша, то подразумевают, что есть некая семья, к членам которой они относятся. Упорядоченная пара (Маша, Саша) отличается от других упорядоченных пар людей тем, что между Машей и Сашей есть некое родство (кузина, отец, и т. д.). В математике среди всех упоря­доченных пар декартового произведения А´В двух множеств А и В тоже выделяются некоторые пары в связи с тем, что между их компонентами есть некоторые «родственные» отношения, которых нет у других.

В качестве примера рассмотрим множество S студентов какого-нибудь техникума и множество D изучаемых там дисциплин. В декартовом произведении S´D можно выделить большое подмножество упорядоченных пар (s, d), обладающих свойством: студент s изучает дисциплину d. Построенное подмножество отражает отношение «изучает», естественно возникающее между множествами студентов и дисциплин.

Для строгого математического описания любых связей между элементами двух множеств вводится понятие бинарного отноше­ния, которое часто появляется как в ма­тематике, так и в информатике. Отношения между элементами не­скольких множеств (n-арные отношения) применяются для описания простой системы управления базами данных.

Отношением (бинарным отношением, двуместным отношением) из множества A в множество B называется некоторое подмножество декартового произведения  

Отношения в дальнейшем будем обозначать

 

(читается  отношение из A в B)

Если  ,   и , то говорят,  что a находится в отношении с b. Используется также запись

 

ПРИМЕР

Если  отношение из  A  в  A   ( ), то говорят  бинарное отношение на множестве A.

ПРИМЕР

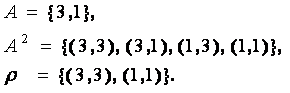
n-арным отношением на множестве А, называется некоторое подмножество n-ой степени множества A.

ПРИМЕР

,      −   n-арное отношение на множестве А.

Виды бинарных отношений на множестве A

1)          Обратное отношение  .

2)          Дополнение                 .

3)          Тождественные             .

4)     Универсальные              .