8.Биномиальные коэффициенты и их свойства.

В математике биномиальные коэффициенты — это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»):

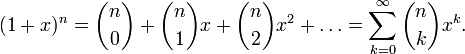
В комбинаторике биномиальный коэффициент интерпретируется как количество сочетаний из n по k, то есть количество всех подмножеств (выборок) размера k в n-элементном множестве.

Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.

Производящие функции

Для фиксированного значения n производящей функцией последовательности биномиальных коэффициентов является:

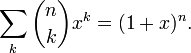
Для фиксированного значения k производящей функцией последовательности биномиальных коэффициентов является:

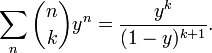
Двумерной производящей функцией биномиальных коэффициентов является:

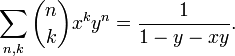
Делимость

Из теоремы Люка следует, что:

• нечётен в двоичной записи числа k единицы не стоят в тех разрядах, где в числе n стоят нули.

• некратен простому p в p-ичной записи числа k все разряды не превосходят соответствующих разрядов числа n.

• В последовательности биномиальных коэффициентов :

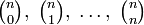  • все числа не кратны заданному простому p 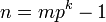, где натуральное число m < p;

  • все числа, кроме первого и последнего, кратны заданному простому p ;

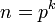  • количество нечётных чисел равно степени двойки (степень двойки равна количеству единиц в двоичной записи числа n);

  • не может быть поровну чётных и нечётных чисел;

  • количество не кратных простому p чисел равно 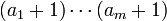, где числа 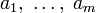 — разряды p-ичной записи числа n; а число 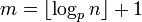— её длина.

Основные тождества

• 

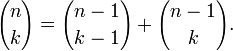
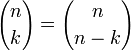• (правило симметрии).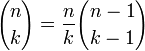

• (вынесение за скобки).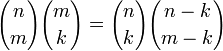

• (замена индексов).

Бином Ньютона и следствия

• 

• 

• 

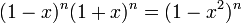
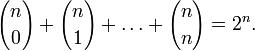
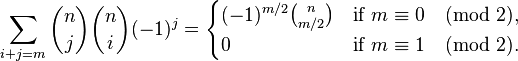
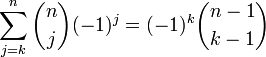• для .

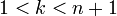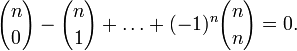• Это тождество можно усилить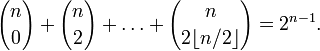

• 

Свёртка Вандермонда и следствия

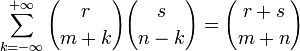• (свёртка Вандермонда).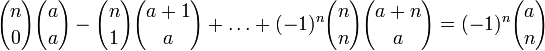

• .

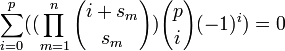• если 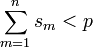— более общий вид тождества выше.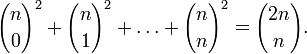

• 

Другие тождества

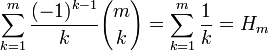• — m-ое гармоническое число.

• Мультисекция ряда даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t 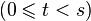в виде замкнутой суммы из s слагаемых:

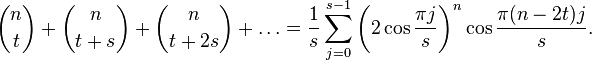
Асимптотика и оценки

• 

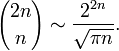
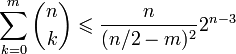• при 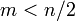(неравенство Чебышёва).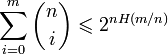

• , при 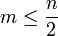(энтропийная оценка),

где  — энтропия.

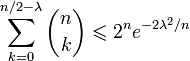• (неравенство Чернова).

9.Обьединение комбинаторных конфигураций.

Для формулировки и решения комбинаторных задач используются различные модели комбинаторных конфигураций (схем). Наиболее популярными являются следующие 2 модели: 1. Дано k предметов. Их нужно разместить по n ящикам так, чтобы выполнялись заданные ограничения. Сколькими способами это можно сделать? 2. Рассмотрим множество функций F: X  Y, где , , . Без ограничения общности можно считать, что , , . Сколько существует функций ^ F, удовлетворяющих заданным ограничениям? Замечание. Все задачи комбинаторики можно переформулировать либо на языке “ящиков”, либо на языке “функций”. В нашем курсе отдадим предпочтение первой модели. Далее рассмотрим различные комбинаторные конфигурации.