
- •Дискретная математика.
- •1.1.Понятие множества.
- •1.2.Подмножество.
- •1.3.Пример множеств. Пустое и универсальное множества.
- •2.Операции над множествами. Дополнение, обьединение,пересечение,разность,симметрическая разность и прямое произведение множеств.
- •3.Алгебраические свойства операций над множествами - коммутативность, ассоциативность, дистрибутивность, идемпотентность, инволюция, поглощение, нейтральность и законы де Моргана.
- •4.Булев куб и его свойства.
- •5.Основные правила комбинаторики.
- •6.Выборки элементов без повторений.
- •7.Выборки элементов с повторениями.
- •8.Биномиальные коэффициенты и их свойства.
- •Производящие функции
- •Делимость
- •9.Обьединение комбинаторных конфигураций.
- •10.Понятие отношений на множествах и способы их задания.
Дискретная математика.
1.1.Понятие множества.
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N, ..., а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n, ... Существуют стандартные обозначения для некоторых множеств. Например,
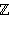 −
множество целых чисел;
−
множество целых чисел;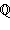 −
множество рациональных чисел;
−
множество рациональных чисел;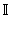 −
множество иррациональных чисел;
−
множество иррациональных чисел;
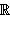 −
множество действительных чисел;
−
множество действительных чисел; −
множество комплексных чисел.
−
множество комплексных чисел.
Если элемент a принадлежит множеству
A, то пишут: a ![]() A.
A.
Множество считается заданным, если для любого объекта можно определить, принадлежит ли этот объект множеству или нет.
1.2.Подмножество.
Множество
![]() является
подмножеством множества
является
подмножеством множества
![]() ,
если любой элемент,
принадлежащий
,
также принадлежит
.
Формальное определение:
,
если любой элемент,
принадлежащий
,
также принадлежит
.
Формальное определение:
![]()
Множество называется надмно́жеством множества , если — подмножество .
1.3.Пример множеств. Пустое и универсальное множества.
Термин "множество" употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить о: а) множестве пчёл в улье, б) множестве точек отрезка, в) множестве вершин квадрата или о множествах его сторон и диагоналей, г) множестве студентов в аудитории и т.д. В приведённых примерах в случаях а), в)-г) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример б)) пересчитать невозможно, поэтому такие множества называются бесконечными. Множество, не содержащее ни одного элемента, называется пустым множеством.
Универса́льное мно́жество —множество, содержащее все мыслимые объекты. Универсальное множество единственно.
Универсальное множество обычно
обозначается
![]() ,
реже
,
реже
![]() .
.
2.Операции над множествами. Дополнение, обьединение,пересечение,разность,симметрическая разность и прямое произведение множеств.
Определение 1.3. Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут A B, где " " есть знак вложения подмножества. Из определения следует, что для любого множества A справедливы, как минимум, два вложения A A и A U.
Определение 1.4. Если A B и A B, A , то A называетсясобственным подмножеством множества B. В этом случае B содержит хотя бы один элемент, не принадлежащий A.
В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества: A.
Пустое множество и само множество A называются несобственными подмножествами множества A.
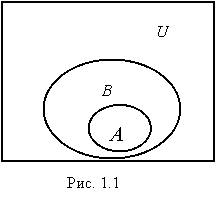
При графическом изображении множеств удобно использовать диаграммы Венна , на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника (рис 1.1).
Определение 1.5.Объединением множеств A и B (обозначение A B) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2). Символически это можно записать следующим образом:
A B = {xx A или x B}.

Определение 1.6. Пересечением множеств A и B (обозначение A B) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3):
A B = {xx A и x B}.
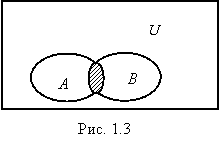
Определение 1.7. Разностью множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B (рис. 1.4):
A\B = {xx A и x B}.
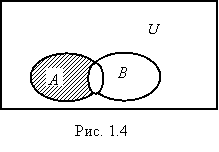
Определение 1.8. Симметрической разностью множеств A и B называется множество A B = ( A\B )( B\A ) (рис. 1.5).
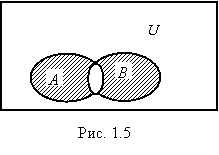
Определение 1.9.
Абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, т.е. множество A = U\A, где U - универсальное множество (рис. 1.6).
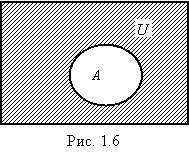
В дальнейшем вместо термина "абсолютное дополнение" мы будем употреблять термин "дополнение".
Пример 1.1. Если U = { a, b, c, d, e, f, g, h }, A = { c, d, e }, B = { a, c, e, f, h }, то
|
A B = { a, d, f, h }, |
A
|
= { a, b, f, g, h }. |
