3. Распределение носителей в базе.
Для того чтобы
рассчитать токи, межэлектродные
напряжения и избыточные заряды в
транзисторе, необходимо знать распределения
избыточных концентраций, т.е. функции
или
.
Эти функции рассматриваются ниже
применительно к бездрейфовому транзистору
типа.
В стационарном режиме концентрация носителей, инжектированных в базу, описывается диффузионным уравнением:
, (4.1)
где
– средняя диффузионная длина.
Общее решение этого уравнения имеет вид:
. (4.2)
Коэффициенты
и
определяются с помощью граничных
условий, характеризующих эмиттерную и
коллекторную границы базы.
При записи граничных
условий для нормального включения
транзистора примем, что на коллекторном
переходе задано обратное напряжение
,
а на эмиттерном переходе – прямой ток
,
точнее – его электронная составляющая
.
Будем считать, что
толщина базы равная
,
расстояние
отсчитывается от эмиттерной границы к
коллекторной, т.е. на границе эмиттер-база
,
а на границе база-коллектор
.
Для определения первого граничного условия воспользуется выражением для плотности тока:
, (4.3)
где
–
площадь эмиттерного перехода диффузии
электронов в базе.
Знак минус в правой части отражает тот факт, что у транзисторов прямой, т.е. положительный ток эмиттера означает инжекцию электронов в базу; при этом градиент их концентрации должен быть отрицательным.
Тогда первое граничное условие запишется как:
,
отсюда
. (4.4)
Полагая
,
получаем из (3.3б)
.
Поскольку в базе
-типа
равновесная концентрация электронов
очень мала, пренебрежем величиной
и запишем второе граничное условия в
виде
,
т.е.
. (4.5)
Решая совместно
уравнения (4.4) и (4.5), можно найти коэффициенты
и
:
;
.
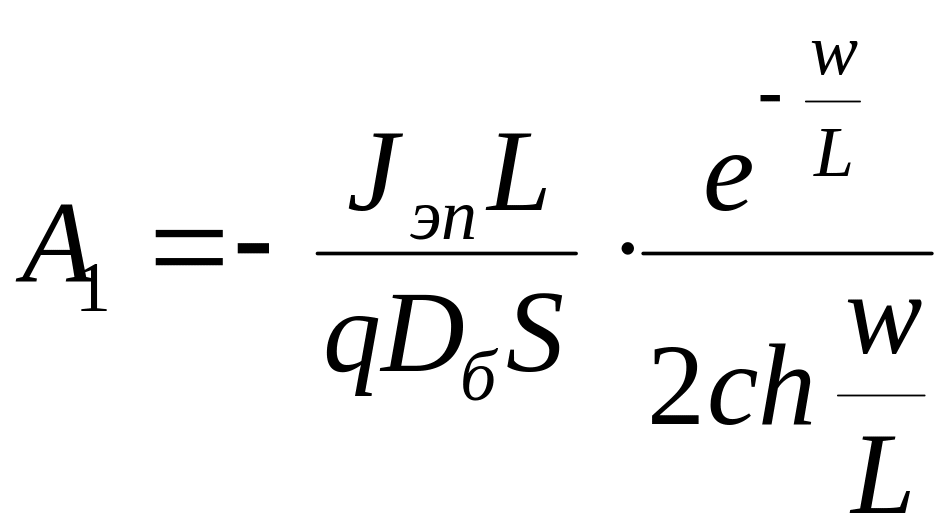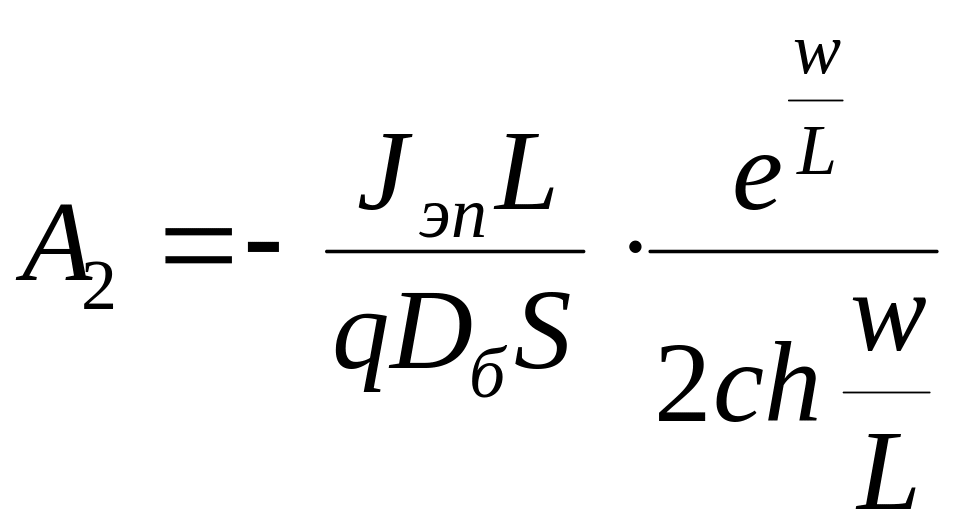Общее решение запишется как:
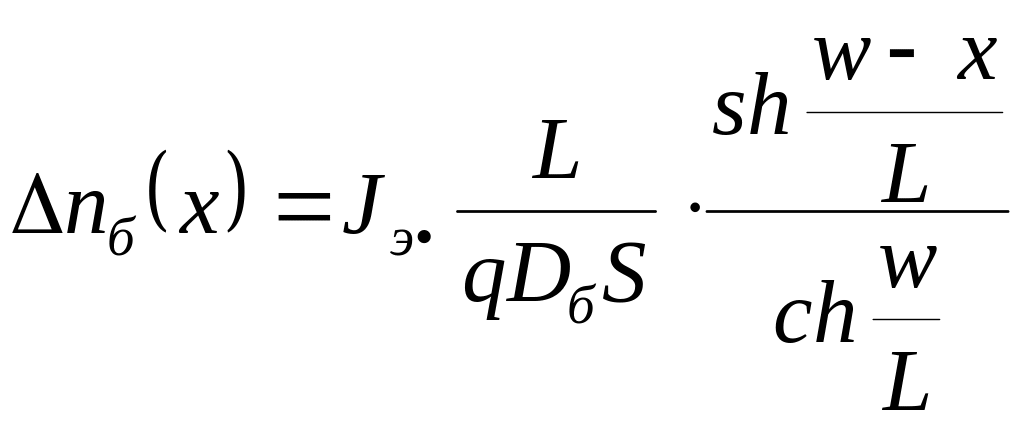. (4.6)
Поскольку в
транзисторах выполняется неравенство
,
полученное выражение можно упростить,
воспользовавшись соотношениями,
действительными для малых аргументов
.
Тогда
. (4.7)
Следовательно, бездрейфовым транзисторам с однородной базой свойственно почти линейное распределение избыточных носителей (рис.4.4).
Интегрируя функцию
в пределах от
до
,
получим величину избыточного заряда
в базе:
. (4.8)
Как видим, избыточный заряд пропорционален току эмиттера, а при заданном токе уменьшается с уменьшением толщины базы.
4. Модуляция толщины базы.
Как известно,
ширина толщины
перехода зависит от напряжения на нем.
Поскольку эмиттерный переход смещен в
прямом направлении, его ширина мала и
изменения этой ширины при изменениях
не имеют существенного значения.
Коллекторный же переход, смещенный в
обратном направлении, имеет сравнительно
большую ширину, и изменения ее при
изменениях напряжения
важны для работы транзистора, а именно,
поскольку коллекторный переход
сосредоточен в базе (как более высокоомном
слое), приращения его ширины оказываются
практически равными приращениям толщины
базы. В результате получается зависимость
,
которую называют модуляцией
толщины базы
или эффектом
Эрли.
Основные следствия этого эффекта:
изменения толщины базы влияет на ту долю инжектированных электронов, которая доходит до коллектора, избежав рекомбинации. Значит при неизменном токе эмиттера модуляция толщины базы приводит к изменениям тока коллектора. Соответственно коэффициент передачи эмиттерного тока оказывается функцией коллекторного напряжения, а коллекторный переход имеет конечное дифференциальное сопротивление;
модуляция толщины базы сопровождается изменением заряда электронов в базе; иначе говоря, имеет место зависимость заряда от коллекторного напряжения, т.е. коллекторный переход обладает некоторой диффузионной емкостью дополнительно к обычной барьерной емкости;
модуляция толщины базы меняет время диффузии электронов через базу, тем самым коллекторное напряжение влияет на частотные свойства транзистора;
поскольку тепловой ток эмиттерного перехода
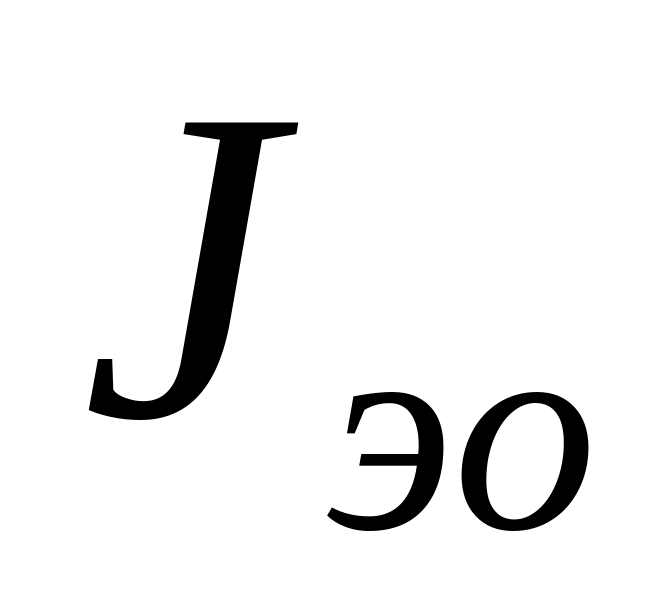при тонкой базе обратно пропорционален
ее толщине ( 3.11б), напряжение
,
модулируя толщину базы, модулирует
также ток
,
а вместе с ним согласно (3.9а) всю
вольтамперную характеристику эмиттерного
перехода. Следовательно, если одна из
входных величин (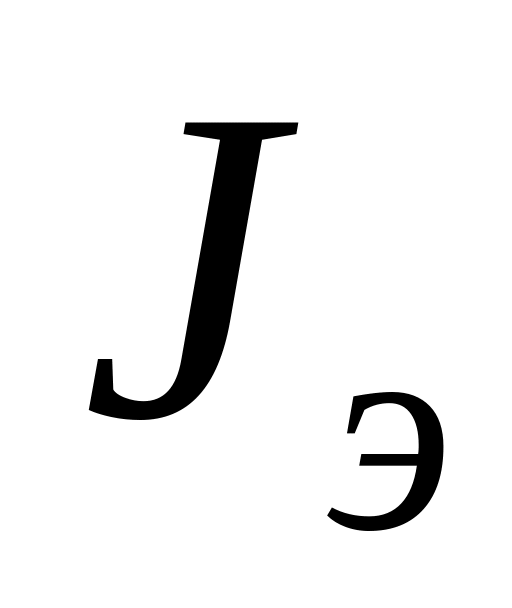
или
)
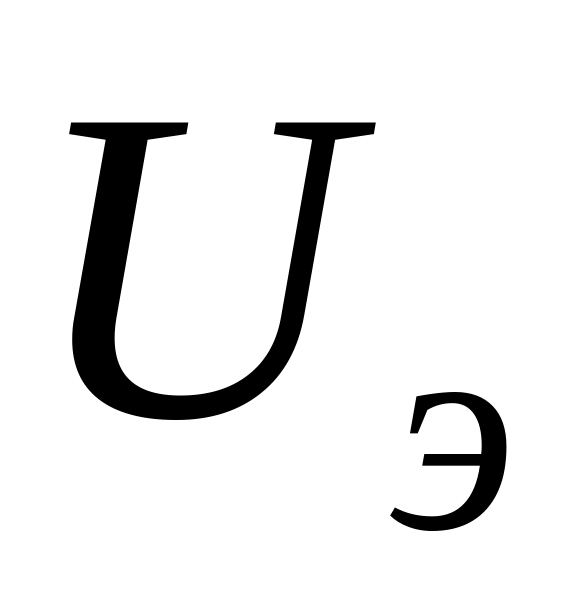задана, то вторая оказывается функцией
коллекторного напряжения. Такое влияние
называют внутренней
обратной связью по напряжению.