Применение первого начала термодинамики к газовым процессам Механическая работа в изопроцессах

Как было отмечено ранее, механическая работа зависит не только от параметров, при которых находится газ в двух состояниях, но и от процесса перехода из одного состояния в другое. Рассмотрим этот вопрос применительно к известным изопроцессам, исходя из того, что полная работа выражается интегрально:

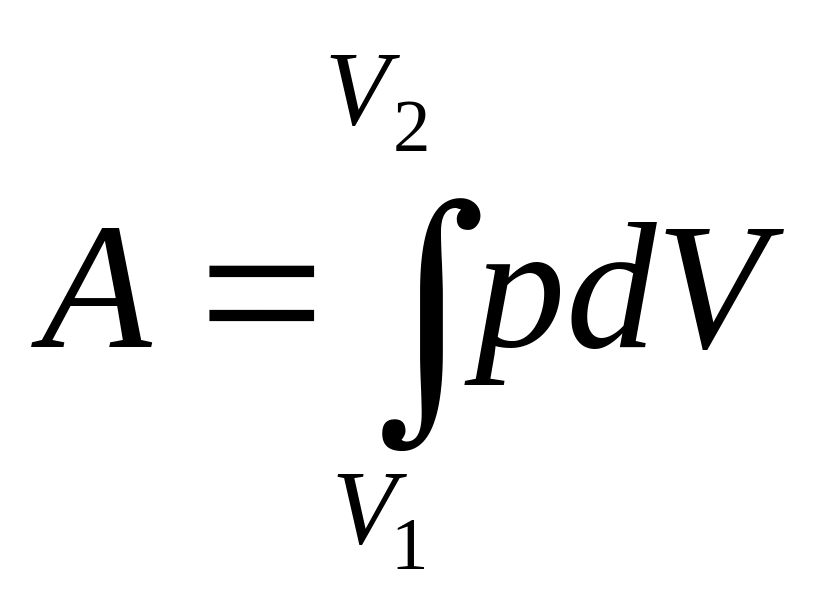
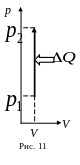, (47)

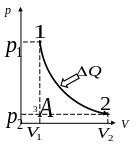
1. Изохорный процесс. Т.к. при V=соnst и dV=0, то и работа А=0. Т.е первое начало термодинамики выглядит dQ=dU. Все подводимое к газу тепло идет на увеличение внутренней энергии. Изохорный процесс на pV–диаграмме изображается вертикальной линией (рис. 11).

2. Изобарный процесс. Поскольку давление остается постоянным, то и сила, действующая на поршень, или стенку сосуда постоянна. Поэтому работу можно выразить следующим образом

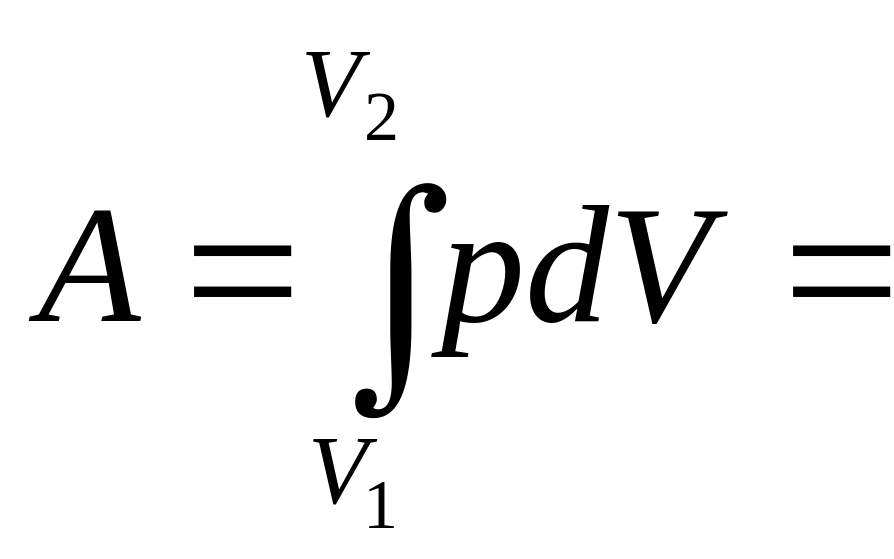
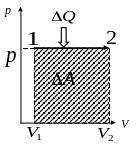
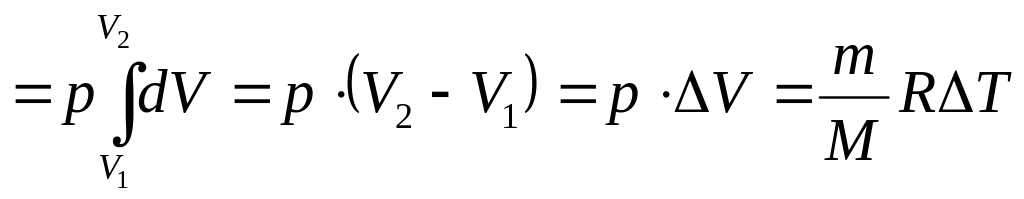,(48)

Е

Рис. 12

стественно, что работу можно найти , используя формулу первого начала термодинамики. При этом подводимое к газу тепло частично тратится на увеличение внутренней энергии (на нагревание) и частично на работу. На pV– диаграмме процесс изображается горизонтальной прямой параллельной оси V, а работа изобразится площадью прямоугольника 12V₂V₁ (рис. 12).

3. Изотермический процесс. В виду того, что температура остается постоянной, удобнее давление выразить из закона Клапейрона– Менделеева и заменить в подинтегральном уравнении работы

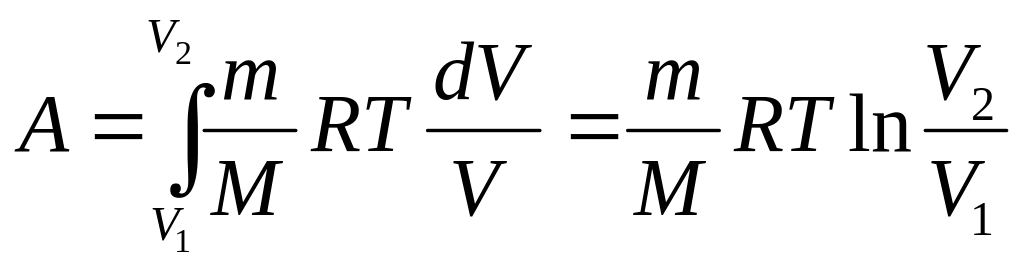
, или ,(49)

О

Рис. 13

тметим еще одно обстоятельство, характерное для этого процесса, а именно, что для этого процесса dU=0, а т.к. dT=0, то для этого процесса dQ=dA. Иначе говоря,если сообщаем газу некоторое количество теплоты, то работа будет совершена большая именно при изотермном процессе (естественно при одинаковых тепловых затратах). Т.е с этой точки зрения изотермный процесс является предельным (получается предельно большая работа). Т.к. на диаграмме pV уравнение изотермического процесса изображается гиперболой, то работа изобразится площадью фигуры 1231 (рис. 13).

При изотермическом процессе увеличение внутренней энергии компенсируется ее уменьшением вследствие совершенной газом работы. Т.о. внутренняя энергия остается постоянной.

Осуществление изотермического процесса предполагает существование (при той же температуре) внешней среды, обладающей огромным запасом внутренней энергии по сравнению с внутренней энергией рабочего газа. Расширение газа должно происходить бесконечно медленно, чтобы его температура успевала выравниваться с температурой··· окружающей среды. Практически всегда можно указать предельную скорость реального процесса, при которой процесс будет близок к изотермическому.

Теплоемкость газов

Обмен теплом между данной газовой (или иной) системой и окружающей средой можно рассчитать на основании первого начала термодинамики, если известно изменение внутренней энергии и работа, совершенна системой (или над системой).

Однако иногда такой обмен удобно рассчитать по формуле

, (50)

где с– удельная теплоемкость тела (газа, жидкости, твердого тела).Физический смысл удельной теплоемкости: количество энергии в форме теплоты, которое нужно сообщить телу, чтобы нагреть единицу массы этого тела на один градус. В системе СИ .

Кроме удельной теплоемкости используется понятие молярной теплоемкости: количество энергии в форме теплоты, которое нужно сообщить одному молю тела, чтобы нагреть его на один градус. В системе СИ .

Таким образом, связь между этими двумя видами теплоемкости:

, (51)

В прикладной теплотехнике используется объемная теплоемкость: количество энергии в форме теплоты, которое нужно сообщить единице объема тела, чтобы нагреть его на один градус. В системе СИ .

Наконец, можно говорить о теплоемкости тела: количество энергии в форме теплоты, которое нужно сообщить всему телу, чтобы нагреть всю массу тела один градус. В системе СИ .

, (52)

Имеется одна особенность, отличающая теплоемкость газов от теплоемкостей других сред – она зависит от процесса , при котором изменяются параметры термодинамической системы. Действительно, заменим в уравнении первого начала термодинамики теплоту и внутреннюю энергию:

, (53)

Из последнего видно, что молярная теплоемкость идеального газа зависит от процесса, при котором происходит передача теплоты , т.к работа в свою очередь зависит от этого. 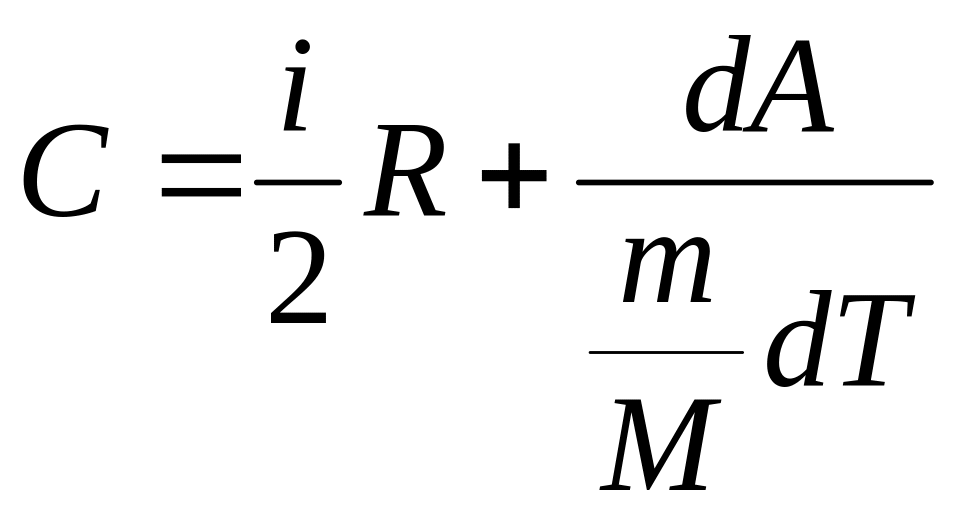, (54)

1. Изохорный процесс. Поскольку при этом процессе работы не совершается, то второе слагаемое в уравнении (93) отсутствует и молярная и удельная теплоемкости принимают вид:

и , (55)

Их называют молярная и удельная теплоемкости газа при постоянном объеме.

2. Изобарный процесс. Подставим в уравнение (44) формулу работы, выраженную через температуру :

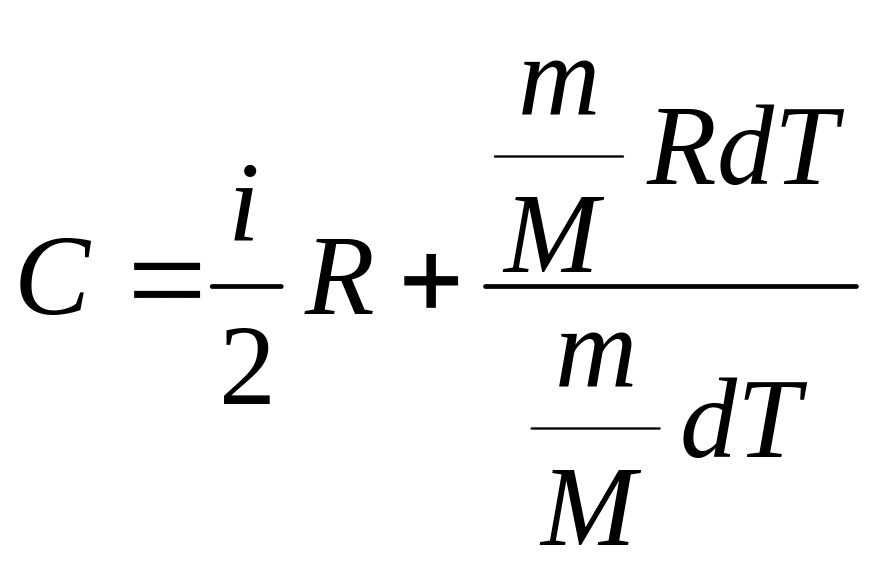
Преобразуя, получаем выражения для молярной и удельной теплоемкостей при постоянном давлении:

и , (56)

Если взять разность молярных теплоемкостей ( при постоянном давлении и постоянном объеме), то получим уравнение Майера

, (57)

Т.о. можно отметить, ч то молярная теплоемкость при постоянном давлении больше молярной теплоемкости при постоянном объеме на величину работы, которую необходимо затратить, чтобы 1 моль газа нагреть на 1⁰ С.

3. Изотермический процесс. Т.к. при этом процессе , то

, (58)

Это означает, что несмотря на подводимую к газу теплоту, газ не нагревается, т.е. так ведет себя тело бесконечно большой массы.