Распределение молекул газа по скоростям

Молекулы газа движутся с самыми различными скоростями, причем численное значение скорости и ее направление все время меняется. В результате при отсутствии внешних воздействий распределение молекул по направлениям будет равномерным, т.к. каждое направление равновероятно.

Другое дело с численными значениями скоростей. Возможные значения скоростей. Заключенных в пределах от нуля до бесконечности, далеко не равновероятны. Дело в том,что скорость равная бесконечности вообще не может иметь места, ибо даже если все молекулы отдадут свою энергию одной молекуле, а сами остановятся, то и в этом случае скорость молекулы будет максимально большой, но не бесконечно большой.

Значит скорость молекул газа не может принимать значений с некоторого до бесконечности.

Т.к. такой процесс совершенно маловероятен, то можно утверждать, что как слишком большие скорости по сравнению со средним значением, так и очень малые значения , будут маловероятны.

Совершенно понятно, что среди огромного числа молекул будут группы молекул с одинаковыми скоростями.

Встает вопрос, каким же образом определить, сколько молекул, имеющих одинаковую скорость приходится на одинаковый интервал.

Английский физик Дж. Максвелл в 1860 г., применив к тепловому хаотическому движению молекул законы теории вероятностей и математической статистики получил закон, который называют закон максвелловского распределения молекул по скоростям. Этот закон описывается некоторой функцией распределения молекул по скоростям. Суть закона сводится к следующему. Если разбить весь диапазон скоростей молекул на малые, но одинаковые интервалы, равные , то на каждый интервал скорости будет приходиться некоторое число молекул , имеющих скорость , заключенную в этом интервале.

Функция определяет относительное число молекул ,скорости которых лежат в интервале от до .

, (36)

Конкретный вид функции зависит от рода газа (от массы молекулы) и от параметров состояния (температуры). График распределения функции по скоростям имеет вид, изображенный на рисунке 8.

Ф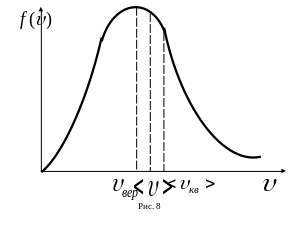 ункция распределения удовлетворяет условию нормиро-вания:

Вся площадь

под кривой равна единице.

Тогда относительное число молекул , скорости которых лежат в интервале от до находится на графике, как площадь фигуры с основанием , расположенном на оси соответствующей скорости.

Кривая не симметрична относительно максимума кривой. Максимум функции распределения соответствует скорости, называемую вероятной.

, или , (38)

Можно отметить, что число молекул, у которых скорость всего в три раза больше вероятной соответствует 0,04% от общего числа молекул, а скорости, превышающие наиболее вероятную в пять раз, наблюдаются у одной из12 миллиардов молекул. Именно это и позволяет в ряде случаев не учитывать разброса в скоростях и считать, что скорости молекул в основном группируются вблизи вероятной и зависит только от температуры и молярной массы газа.

Кроме вероятной и квадратичной скорости в ряде процессов используется средняя арифметическая скорость.

, или , (39)

При изменении температуры значение максимума функции распределения и вероятной скорости меняется. Значения средней арифметической скорости и среднеквадратичной скорости больше чем вероятной скорости , но их функция распределения меньше

Проведенные эксперименты полностью подтвердили распределение Максвелла, полученное теоретически.