Уравнение состояние идеального газа (уравнение Клапейрона- Менделеева)

На практике преобладают изменения состояния газа, когда меняются не два параметра, а сразу все три параметра.

Закон, описывающий такие процессы, был установлен в 1834 г. Клапейроном на основании эмпирических законов Бойля–Мариотта и Шарля.

П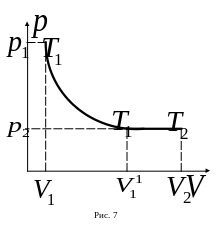 редположим, что имеется некоторая масса газа с исходными параметрами состояния и необходимо перевести газ в состояние с параметрами (рис. 7). Переводим газ из первого состояния в новое промежуточное газовое состояние с параметрами сначала через изотермический процесс, оставляя постоянной температуру и изменяя объем газа до значения . Используя формулу изотермического процесса получаем

, (10)

Графическое изображение процессов представлено на чертеже.

Объединяя формулы (10) и (11), получаем

Затем, используя изобарный процесс ,переводим газ из состояния с параметрами в состояние с параметрами

, (11)

, (12)

Написанная закономерность справедлива не только, когда одно из состояний соответствует нормальным условиям, но и для любого состояния данной массы газа и значит

это уравнение Клапейрона, (13)

Т. к. при данном давлении и температуре объем газа пропорционален массе газа, то и отношение должно быть пропорционально массе, а, следовательно, числу молекул в газе:

, (14)

где k– постоянная Больцмана ( Дж/К).

Число молекул в газе получим, используя число молей газа и число Авогадро:

, (15)

Подставляя (15) в (14) получаем:

, (16)

Произведение Дж/(моль∙К) называют универсальной газовой постоянной.

Тогда окончательно уравнение (16) принимает вид

, (17)

Которое и называют уравнением состояния идеального газа или уравнение Клапейрона–Менделеева.

Универсальная газовая постоянная имеет вполне определенный физический смысл: она численно равна работе расширения одного моля газа при его нагревании на один градус при постоянном давлении.

1 моль газа равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде –12 массой 0,012 кг.

Основное уравнение молекулярно-кинетической теории газов

С молекулярно- кинетической точки зрения давление газа на стенки сосуда обусловлено ударами молекул о них и должны быть связаны с величинами, определяющими движение отдельных молекул (их массами и скоростями).

Для установления такой связи представим, что в сосуде находятся молекулы одноатомного газа, имеющие различные скорости .

Пренебрегая полем тяготения, каждая молекула при ударе о стенку сосуда действует на нее с силой, зависящей от нормальной составляющей скорости. Любая скорость может быть разложена на три компоненты, соответствующие проекции этой результирующей скорости на соответствующую ось. Так, например, скорость молекулы представляется

, (18)

Т.о. если ось Х перпендикулярна стенке сосуда, то для молекулы массой , подлетающей к стенке со скоростью и испытавшей абсолютно упругое столкновение, можно написать, что

, (19)

Если в направлении оси Х в обе стороны движутся молекулы имеющие скорость , то за время об эту стенку площадью S ударятся все молекулы, находящиеся в объеме c основанием S и высотой . Общий импульс силы запишется следующим образом

, (20)

или , (21)

где число молекул в единице объема (концентрация), имеющих скорость . Величина ½ в уравнении (2) отражает тот факт, что количество молекул, движущихся вдоль оси Х в направлении стенки равно половине от всех молекул по этой оси.

Тогда давление, оказываемое эти ,,сортом” молекул

, (22)

Аналогично для других молекул перемещающихся вдоль этой оси

, ,… (23)

Сложив левые и правые части последних двух уравнений получим

, (24)

Разделим последнее уравнение на – общее число молекул в единице объема ( )

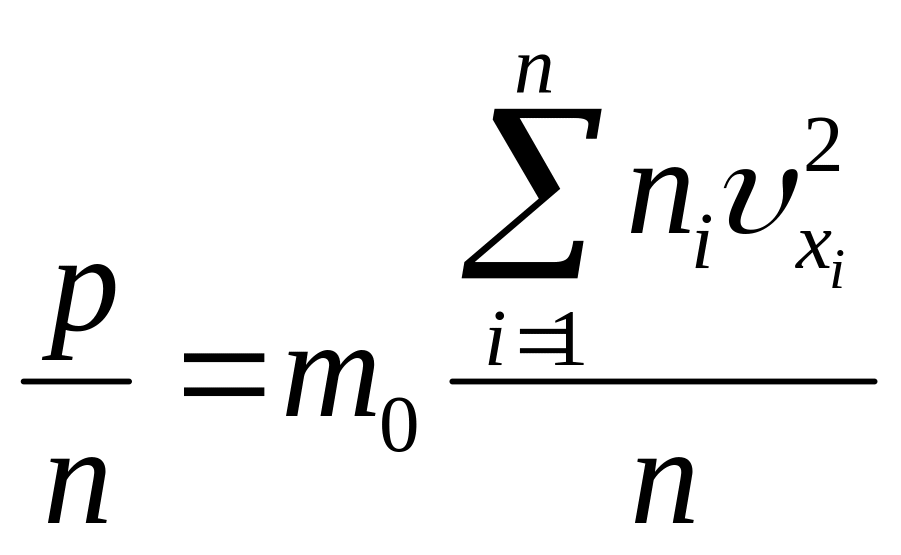
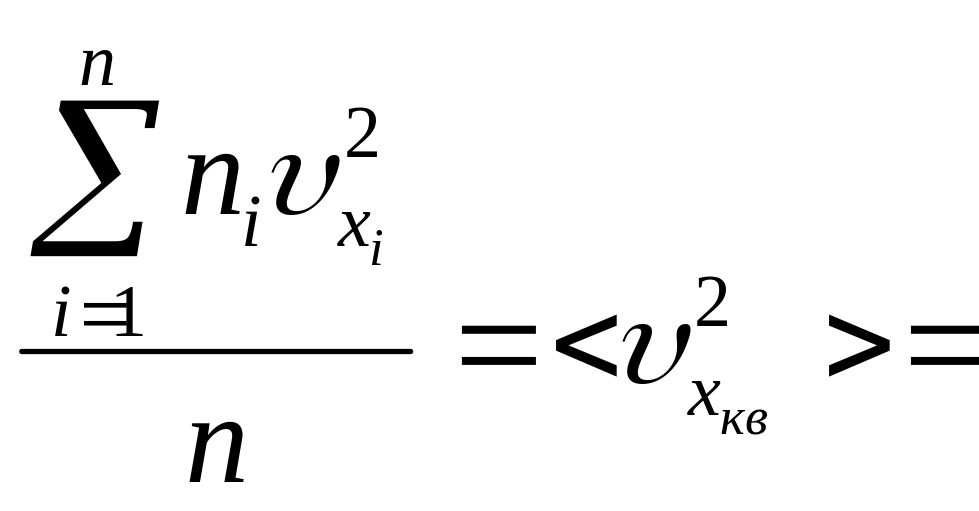
Величина 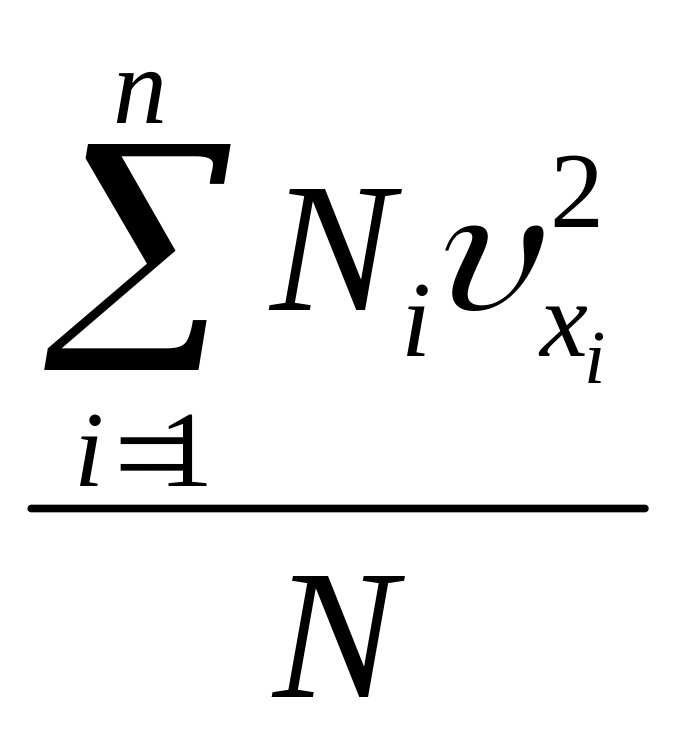представляет некоторое среднее значение квадратов компонент скоростей вдоль оси Х.

Тогда получаем

, (25)

Использование последнего уравнения затруднено тем, что в него входит не полная компонента молекулярной скорости, а ее компонента по оси х.Однако можно написать следующую систему уравнений

……………………….

Умножим левую и правую части каждого уравнения на число молекул, соответствующих скоростям и сложим левые и правые части:

,(26)

Разделим левую и правую части уравнения на общее число молекул.

Тогда получим

, (27)

Т.к. при хаотическом движении нет преимущественных направлений и все они равновероятны, то можно написать, что

, (28)

С учетом этого получаем и подставляя это в (25)

Получаем окончательный вид основного уравнения кинетической теории

, (29)

Из него вытекает

, (30)

Но величина это средняя кинетическая энергия поступательного движения молекулы. С учетом этого уравнение (30) приобретает вид

, (31)

Это уравнение Клаузиуса.

Умножим левую и правую части уравнения (31) на объем одного моля газа : , в котором число Авогадро,

а . Тогда , а отношение

В результате получаем, что энергия поступательного движения молекулы выражается через температуру:

, (32)

Определение температуры как параметра состояния газа должно основываться на такой физической величине, которая автоматически определяет состояние системы. Ею и является средняя кинетическая энергия поступательного движения молекулы

,

Заменяя в уравнении (31) получаем зависимость давления от температуры

, (33)

Используя формулу (32) можно получить формулу для среднеквадратичной скорости молекулы

Отсюда , (34)

Если заменить постоянную Больцмана, а масса молекулы

то , (35)