Примеры решения задач

Задача 1.

При давлении P_н = 15,55∙10⁵ Па в трубе происходит пузырьковое кипение воды, которая движется со скоростью w = 2,2 м/с. Температура стенки трубы t_ст = 213 ^оС. Длина трубы ℓ = 2м, диаметр d_тр 34×2мм. Найти тепловой поток, передаваемый от стенки к воде.

Решение.

Тепловой поток, передаваемый от стенки трубы к кипящей жидкости в условиях вынужденной конвекции

Q = ā ∙ (t_ст – t_н ) F,

где - среднее значение коэффициента теплоотдачи, учитывающее одновременное влияние кипения и вынужденной конвекции на интенсивность теплоотдачи.

Эта формула справедлива при 0,5 ≤ α_к / α_w ≤ 2,

при α_к / α_w < 0,5, ā = α_w;

при α_к / α_w > 2, ā = α_к

α_w – коэффициент т/о при вынужденном движении жидкости, при отсутствии влияния кипения,

α_к – коэффициент т/о при кипении в условиях свободного объема (при отсутствии вынужденной конвекции).

Значение α_w определим по известным критериальным уравнениям конвективного теплообмена.

При определяющей температуре t_н= 200^оС, соответствующей P_н=15,55∙10⁵ Па, выбираем необходимые свойства воды

υ_ж = 0,158∙10^-6 м²/с, λ_ж = 0,663 Вт/(м∙К), Pr_ж = 0,93, Pr_ст = 0,9

Режим движения воды в трубе определим по критерию Рейнольдса

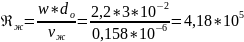- развитый турбулентный режим течения

(d_о = d_тр – 2 δ = 34 – 2 ∙ 2 = 30мм).

Коэффициент теплоотдачи α_w определим по критериальному уравнению М. Михеева

Nu_ж = 0,021 ∙ Re_ж^0,8 Pr_ж^0,43 ∙ (Pr_ж / Pr_ст)^0,25 ∙ ε_l

При l/d_о = 2 / 0,03 = 66,7 > 50, ε_l = 1

Nu_ж = 0,021 ∙ (4,18 ∙ 10⁵)^0,8 (0,93)^0,43 ∙ (0,93 / 0,9)^0,25 ∙ 1 = 659,5

Коэффициент теплоотдачи будет равен

Коэффициент теплоотдачи α_к определим по формуле для кипения в свободном объеме

α_к = 38,7 ∙ (t_ст - t_н)^2,23 ∙ P_н^0,15 = 38,7 ∙ (213 – 200)^2,23 15,55^0,15 = 6 ∙ 10⁴ Вт/(м²К)

здесь P_н , бар

В нашем случае соотношение,

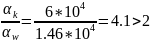
Тогда

ā = α_к

А тепловой поток определится, как

Q = α_к ∙ (t_ст – t_н ) F = 6 ∙ 10⁴ ∙ (213 – 200) ∙ 3,14 ∙ 0,034 ∙ 2 = 1,67 ∙ 10⁵ Вт

Задача 2.

В конденсаторе на горизонтальной трубе с наружным диаметром d_тр = 18мм конденсируется влажный водяной пар со степенью сухости х = 0,9 при давлении P_н = 0,476 МПа. Найти средний по окружности трубы коэффициент теплоотдачи и количество пара, конденсирующегося за час на 1м длины трубы, имеющей температуру стенки t_ст = 140 ^оС.

Решение.

Среднее значение коэффициента теплоотдачи при конденсации на горизонтальной трубе находим по формуле Нуссельта

где свойства теплоносителя (жидкости) выбираем по средней температуре пленки конденсата (кроме значения r, которое выбирается при температуре насыщения)

t_ж = 0,5 ∙ (t_н + t_ст)

Температуру насыщения водяного пара определяем по давлению насыщения.

P_н = 0,476 МПа, t_н = 150 ^оС, r = 2,114 ∙ 10⁶ Дж/кг

t_ж = 145 ^оС, при этой температуре λ_ж = 0,685 Вт/(м∙К), ρ = 922 кг/м³,

μ = 198 ∙ 10^-6 Па∙с

Количество образующегося конденсата определяем из уравнения теплового баланса.

G_гор ∙ r = α_гор ∙ (t_н - t_ст) ∙ F

F = π ∙ d ∙ l

l = 1м

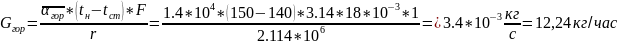
Задача 3.

Рассчитать средний коэффициент теплоотдачи, количество конденсирующегося пара в час на 1 м трубы, если в условиях задачи 2 труба будет расположена вертикально. Сравнить результаты с горизонтальным расположением трубы, если в обоих случаях течение пленки ламинарное.

Решение.

При конденсации на вертикальной трубе среднее значение коэффициента теплоотдачи рассчитываем по соответствующему уравнению Нуссельта

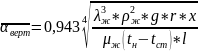
(l = 1м – высота трубы)

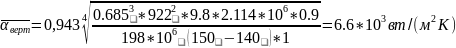
Количество образующегося конденсата

Вывод: при конденсации на вертикальной трубе интенсивность теплоотдачи ниже, а количество конденсирующегося пара меньше чем на горизонтальной трубе при прочих равных условиях.

Задача 4.

Секционный противоточный теплообменник типа «труба в трубе» предназначен для охлаждения жидкого аммиака после конденсатора. Диаметр внутренних труб 38 × 3,5мм и наружных 57 × 3мм; трубы стальные.

В теплообменнике требуется охладить 0,152 кг/с аммиака от температуры t_a1 = t_н = 35,6 ^оС, соответствующей состоянию насыщенной жидкости, до температуры t_a2 = 27 ^оС. Температура охлаждающей воды на входе в аппарат t_в1 = 25 ^оС, на выходе из него t_в2 = 29 ^оС. Вода движется по внутренним трубам, аммиак охлаждается в межтрубном пространстве.

Определить поверхность теплообменника, а также подобрать длину секций и количество секций.

Расчет осуществить для чистой поверхности и при наличии загрязнений в виде слоя масла δ_м = 0,05мм (λ_м = 0,139 Вт/(м∙К)) и слоя водяного камня δ_к=0,5мм (λ_к = 1,745 Вт/(м∙К))

Решение. Определяем среднюю логарифмическую разность температур в аппарате по формуле для противотока

Тепловая нагрузка аппарата

Q = G_a· с_а · (t_а1 – t_а2) = 0,152 · 4,81 · (35,6 – 27) = 6,29кВт

Удельную теплоемкость жидкого аммиака находим по средней температуре между входом и выходом из теплообменника

t_а = 0,5·(t_а1 + t_а2) = 0,5·(35,6 + 27) = 31,3 ^оС

с_а = 4,81 кДж/(кг · К)

Расход охлаждающей воды определим из уравнения теплового баланса

где удельная теплоемкость воды с_в = 4,19 кДж/(кг · К)

Находим среднюю температуру воды в аппарате. Так как водяной эквивалент воды больше, чем эквивалент аммиака, то среднюю температуру находим как среднюю арифметическую

t_в = 0,5·(t_в1 + t_в2) = 27 ^оС

Средняя температура аммиака

t_а = t_в + ∆t = 27 + 3,9 = 30,9 ^оС

Скорость воды в аппарате

Плотность воды ρ_в = 1000кг/м³

Определяем коэффициент теплоотдачи со стороны воды. Для этого при средней температуре t_в = 27 ^оС находим физические характеристики воды:

υ_в = 0,865∙10^-6 м²/с, λ_в = 61,2∙10^-2 Вт/(м∙К), Pr_в = 5,9

Рассчитаем критерий Рейнольдса:

Таким образом, для воды характерно развитое турбулентное движение, при котором уравнение подобия имеет вид

Температура стенки t_ст неизвестна. Поэтому находим ее в первом приближении как среднюю арифметическую из средних температур воды и аммиака:

t_ст = 0,5·(t_в + t_а) = 0,5·(27 + 31) = 29 ^оС

Pr_ст = 5,6

Тогда

Nu_в = 0,021 ∙ 17850^0,8 ∙ 5,9^0,43 ∙ 1 = 115

Коэффициент теплоотдачи со стороны воды

Скорость жидкого аммиака в аппарате

D_вн = 0,058 – 2 · 0,0035 = 0,051

Определяем коэффициент теплоотдачи со стороны жидкого аммиака.

При t_а = 31 ^оС, υ = 0,221∙10^-6 м²/с, λ = 0,47 Вт/(м∙К), Pr_а = 1,335

Эквивалентный диаметр сечения для прохода аммиака:

d_экв = D_вн – d_нар = 0,051 – 0,038 = 0,013м

тогда

- (развитый турбулентный поток).

Здесь, как и в случае воды, влиянием температуры стенки можно пренебречь

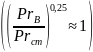
Nu_а = 0,021 ∙ Re_а^0,8 Pr_а^0,43 = 0,021∙16600^0,8 ∙ 1,335^0,43 = 57,2

Коэффициент теплопередачи, отнесенный к внутренней поверхности трубы, омываемой водой:

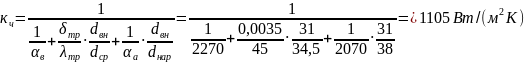
С учетом загрязнений коэффициент теплопередачи будет равен

Теплопередающая поверхность аппарата:

Общая длина и число труб:

L_ч = F_ч / π · d_вн = 15м (6 труб по 2,5м длиной)

L_з = F_з / π · d_вн = 24,6м (10 труб по 2,5м длиной)