53. Непрерывная случайная величина. Закон распределения вероятностей и основные числовые характеристики.
Функцией
распределения вероятностей
называют функцию
,
определяющую вероятность того, что
случайная величина
в
результате испытания примет значение,
меньшее
,
то есть:
.
Случайную
величину называют непрерывной,
если ее функция распределения вероятностей
есть непрерывная, кусочно-дифференцируемая
функция с непрерывной производной.
Свойства функции распределения вероятностей случайной величины
1.
Значения
функции распределения вероятностей
принадлежат отрезку
:
.
2.
Функция
распределения вероятностей – неубывающая
функция, то есть:
,
если
.
Следствие
1.
Вероятность того, что случайная величина
примет значение, заключенное в интервале
,
равна приращению функции распределения
вероятностей на этом интервале:
.
Следствие
2.
Вероятность того, что непрерывная
случайная величина примет одно
определенное значение, равна нулю.
Используя
последнее следствие, легко убедиться
в справедливости следующих равенств:
.
3.
Если
возможные значения непрерывной случайной
величины принадлежат интервалу
,
то:
,
если
;
,
если
.
Следствие.
Если
возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения:
;
.
Плотностью
распределения вероятностей
непрерывной случайной величины
называют
функцию
–
первую производную от функции распределения
вероятностей
:
.
Таким
образом, функция распределения
вероятностей является первообразной
для плотности распределения
вероятностей.
Теорема.
Вероятность того, что непрерывная
случайная величина
примет
значение, принадлежащее интервалу
,
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
.
Следовательно,
зная плотность распределения вероятности
,
можно найти функцию распределения
по
формуле
.
Свойства плотности распределения вероятностей
1.
Плотность
распределения вероятностей –
неотрицательная функция:
.
2.
Несобственный
интеграл от плотности распределения
вероятностей в пределах от
до
равен
единице:
.
Вероятностный
смысл плотности распределения вероятности.
Вероятность того, что непрерывная
случайная величина примет значение,
принадлежащее интервалу
,
приближенно равна (с точностью до
бесконечно малых высшего порядка
относительно
)
произведению плотности распределения
вероятности в точке на длину интервала
:
.
Числовые характеристики непрерывных случайных величин
Математическим
ожиданием непрерывной случайной величины
,
возможные значения которой принадлежат
отрезку
,
называют определенный интеграл
.
Если
возможные значения принадлежат всей
числовой оси, то
(предполагается,
что несобственный интеграл, стоящий в
правой части равенства, существует).
Дисперсией
непрерывной случайной величины
называют математическое ожидание
квадрата ее отклонения.
Если возможные
непрерывной случайной величины
принадлежат
отрезку
,
то
.
Если
возможные значения принадлежат всей
числовой оси, то
(предполагается,
что несобственный интеграл, стоящий в
правой части равенства, существует).
Средним
квадратическим отклонением непрерывной
случайной величины
называют, как и для величины дискретной,
квадратный корень из дисперсии:
.
В задачах практики встречаются непрерывные СВ, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала. Кроме того известно, что в пределах этого интервала все значения СВ обладают одной и той же плотностью вероятности. О таких случайных величинах говорят, что они распределяются по закону равной вероятностиили закону равномерной плотности. [5]
Приведем пример случайной величины, распределенной с равномерной вероятностью.
Поезда метрополитена идут с интервалом 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Т,в течение которого ему придется ждать поезда, представляет собой СВ, распределенную с равномерной плотностью на участке (0, 2) минут.
Рассмотрим СВ X, подчиненную закону равномерной плотности на участке от а до в (см. рисунок 5.6). Плотность этой величины f (x) постоянна и равна с на отрезке (а, в); вне этого отрезка она равна нулю:
(5.29)
Так как площадь, ограниченная кривой распределения, равна единице: c (в-а)=1. Отсюда получаем:c=1/(в-а).
Поэтому плотность распределения f (x) примет вид:
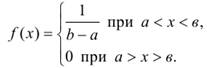(5.30)
Рисунок 5.6 — График равномерной плотности распределения
Эта формула и выражает закон равномерного распределения вероятностей (закон равномерной плотности) на участке (а, в).
Напишем выражение для функции распределения F (x), которая выражается площадью, ограниченной кривой распределения и осью абсциссы, лежащей левее точки х (рисунок 5.6):
(5.31)
График функции распределения F (x) приведен на рисунке 5.7.
Основные числовые характеристики СВ X на участке от а до в:
— математическое ожидание величины X:
Рисунок 5.7 — Функция распределения
— дисперсия величины X:
— среднее квадратическое отклонение:
Найдем вероятность попадания СВ X распределенной по закону равномерной плотности, на участок (х1, х2), представляющий собой часть участка (а, в) (рисунок 5.8).
Рисунок 5.8 — Вероятность попадания величины X на участок(х1, х2)
Геометрически, как это видно из рисунка 5.8, вероятность представляет собой заштрихованную площадь и равна:
