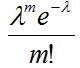51. Понятие случайной величины. Закон распределения дискретных случайных величин.

Случайная величина - одно из основных понятий теории вероятностей. В самом общем смысле случайная величина - это некоторая переменная, принимающая, те пли иные значения с определенными вероятностями. Так, например, число очков, выпадающее на верхней грани игральной кости, может оказаться равным 1, 2, 3, 4, 5, 6 с вероятностями 1/6 для каждого значения. Строгое математическое определение случайной величины как измеримой функции, заданной на некотором вероятностном пространстве, дается в рамках общепринятой аксиоматики теории вероятностей. Именно, для вероятностного пространства (Ω, А, Ρ) так определяется любая однозначная действительная функция X(ω), определенная для ω принадлежащая Ω и такая, что для всех действительных значений x множество {ω : X(x)<x} принадлежит σ-алгебре A (см. "Теория вероятностей").

Важнейшей характеристикой случайной величины ξ служит ее распределение вероятностей. Если различные значения ξ образуют конечную или бесконечную последовательность, то распределение вероятностей ξ задается указанием этих значений x₁, x₂, ..., x_n, ... и соответствующих им вероятностей p₁, p₂, ..., p_n, ..., то есть вероятностей всех событий {ξ=x_k}. Случайные величины указанного типа называются дискретными. Во всех других случаях распределение вероятностей задается указанием для каждого действительного значения x вероятности P{ξ<x} или каждого интервала (a, b) значений ξ вероятности P{a < ξ < b}. Важную роль играют случайные величины, для которых определена такая неотрицательная функция p(x) на прямой, что для любого интервала (a, b) причем , Случайная величина этого типа называется непрерывной, а функция p(x) называется плотностью вероятности.

Таким образом, случайная величина может быть: дискретной (дискретно распределенной), когда она может принимать конечное или бесконечное счетное множество значений, элементы которого могут быть занумерованы и выписаны в последовательность x₁, x₂, ..., x_n, ...; непрерывной (непрерывно распределенной), когда она может принимать любые значения в одном или нескольких заданных интервалах или областях плоскости или пространства (существенным здесь является то обстоятельство, что эти значения образуют несчетное бесконечное множество, которое называют континуумом).

Наиболее полную информацию о распределении вероятности дают функция распределения и характеристическая функция случайной величины. Ряд общих свойств распределения вероятностей в достаточно полной степени описывается небольшим количеством числовых характеристик, среди которых наиболее употребительны математическое ожидание (среднее значение) m_x и дисперсия σ_x² (среднеквадратичное отклонение σ). Кроме указанных характеристик также используются момент, медиана, квантили и семиинварианты. Значениями случайной величины могут быть не только действительные числа, но и векторы, комплексные числа и другие объекты. Обобщением понятия случайной величины служит понятие случайного элемента какого-либо функционального пространства.

 Законы распределения дискретных случайных величин

Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения.

При табличном способе задания закона распределения первая строка таблицы содержит возможные значения случайной величины (обычно в порядке возрастания), а вторая – соответствующие вероятности ( ):

xi	x1	x2	…	xn
pi	p1	p2	…	pn

Бернулли: Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n  с  вероятностями, вычисляемыми по формуле Бернулли:

xi	0	1	…	m	…	n
pi	qn		…		…	pn

где q=1-p;    - число сочетаний из n элементов по m.

Пример 2. На некотором участке дороги 60% водителей соблюдают предусмотренный правилами скоростной режим. Составить закон распределения числа водителей, соблюдающих установленные ограничения по скорости, из пяти проехавших.

Случайная величина Х – число водителей, соблюдающих установленные ограничения по скорости из пяти проехавших. В n=5 независимых испытаниях вероятность того, что скоростной режим не нарушен, по условию постоянна и равна: p=0,6. Следовательно, вероятность нарушения: q=1-0,6=0,4. Тогда биномиальный закон распределения числа водителей имеет вид:

xi	0	1	2	3	4	5
pi	0,01024	0,0768	0,2304	0,3456	0,2592	0,07776

Пуассона: Дискретная случайная величина имеет закон распределения Пуассона с параметром , если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, … с вероятностями, вычисляемыми по формуле Пуассона. Т. к. вероятность наступления события в каждом испытании мала (при ), закон распределения Пуассона еще называют законом редких событий.

xi	0	1	…	m	…
pi			…		…

Пример 3. Вероятность попадания в цель при одном выстреле равна 0,015. Сделано 600 выстрелов. Какова вероятность того, что число попаданий в цель не меньше 7 и не большее 10?

В данном случае . Предполагая закон распределения Пуассона, имеем:

xi	7	8	9	10
pi	0,1171	0,1318	0,1318	0,1186

Следовательно, .

Гипергеометрическое: Говорят, что случайная величина   имеет гипергеометрическое распределение с параметрами ,   и  , где  ,  , если   принимает целые значения  такие, что  ,  , с вероятностями . Случайная величина с таким распределением имеет смысл числа белых шаров среди  шаров, выбранных наудачу и без возвращения из урны, содержащей  белых шаров и  не белых.

Пример 4. В партии из N изделий имеется M (M < N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначимx. Распределение такой случайной величины называется гипергеометрическим и имеет вид:

, k = 0, 1, …, min(n,M),  ,

,  .