43.Линейные дифференциальные уравнения первого порядка

Определение. Уравнение вида y'+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.

Умножим исходное уравнение на интегрирующий множитель -

:

 

Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (1):

Интегрируем:

Умножаем на    . Получаем общее решение линейного дифференциального уравнения первого порядка:

 

Пример решения линейного дифференциального уравнения первого порядка

Решить уравнение:

Решение. Разделим на x:

 

(2)

тогда

 

Интегрирующий множитель:

Знак модуля можно опустить, поскольку интегрирующий множитель можно умножать на любую постоянную (в том числе на ±1).

Умножим (2) на x³

или

Интегрируем:

Делим на x³:

Ответ:

Метод введения двух функций (Бернулли)

Ищем решение исходного уравнения в виде произведения двух функций:

y = u·v

где u, v - функции от x. Дифференцируем:

y' = u'·v + u·v'

Подставляем в исходное уравнение:

Выносим u за скобки:

(1)

В качестве v возьмем любое, отличное от нуля, решение уравнения:

(2)

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx, делим на v:

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. Тогда

Потенцируем и опускаем знак модуля (это сводится к умножению на постоянную ±1)

Подставим в (1) учитывая, что согласно (2) выражение в скобках равно нулю:

Отсюда

Интегрируем

Окончательно находим:

 

Пример решения линейного дифференциального уравнения первого порядка методом Бернулли

Решить уравнение:

Решение.

Делаем подстановку:

y = u·v

где u, v - функции от x. Дифференцируем:

y' = u'·v + u·v'

Подставляем в исходное уравнение:

Выносим u за скобки:

 

(3)

 

В качестве v возьмем любое, отличное от нуля, решение уравнения:

(4)

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx, делим на xv:

Интегрируем:

Постоянную C возьмем равной нулю, поскольку нам нужно любое, отличное от нуля, решение. Тогда

Или

Потенцируем и опускаем знаки модуля (это сводится к умножению на постоянную ±1)

Подставим в (3) учитывая, что согласно (4) выражение в скобках равно нулю:

Отсюда

Интегрируем, применяя формулу :

Окончательно находим:

Ответ:

Метод вариации постоянной (Лагранжа)

Ищем решение однородного уравнения:

Это уравнение с разделяющимися переменными

Разделяем переменные - умножаем на dx, делим на y:

Интегрируем:

Интеграл по y - табличный:

Тогда

Потенцируем:

Заменим постоянную e^C на C и уберем знак модуля, что сводится к умножению на постоянную ±1, которую включим в C:

 

(1)

 

Теперь считаем, что постоянная C является функцией от x:

Находим производную:

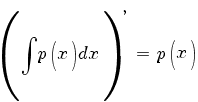
По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в исходное уравнение:

Два члена сокращаются. Отсюда

Интегрируем:

Где C₁ - постоянная интегрирования. Подставляем в (1):

Заменим постоянную C₁ на C. В результате получаем общее решение линейного дифференциального уравнения первого порядка: