
- •Содержание:
- •Построение компьютерной модели расчёта траектории неуправляемого ла (с заданными характеристиками) Анализ и представление исходных данных
- •Модель динамики неуправляемого ла Движение ла по направляющим
- •Активный участок
- •Пассивный участок
- •Алгоритмы численного интегрирования
- •Решение задачи построения модели для одного шага интегрирования методами Эйлера и Рунге-Кутта Начальные условия
- •Расчет системы уравнений методом Эйлера
- •Расчет системы уравнений методом Рунге-Кутта
- •Сравнение решений тестового примера на 1 шаг, полученных без пк
- •Исследовательская часть
- •Программа расчета методом Рунге Кутта:
- •Промежуточные вычисления:
- •Промежуточные вычисления:
- •Список использованных источников:
Пассивный участок
Рассмотрим уравнения движения в проекциях на касательную и нормаль траектории:
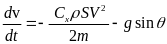 ,
,
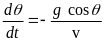 ,
,
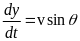 ,
,
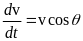 ,
,
Эта система уравнений интегрируется при следующих начальных условиях:
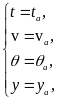
где индекс «а» обозначает конец активного участка. Конечные значения активного участка становятся начальными значениями пассивного участка. Условие окончания интегрирования: y = 0.
При расчете пассивного участка полета ЛА используется ряд допущений, а именно:
Реактивная сила R равна нулю (R=0).
Поверхность Земли представляется в виде бесконечной плоскости.
Масса ЛА постоянна (
 =const).
=const).
Алгоритмы численного интегрирования
Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Если искомая (неизвестная) функция зависит от одной переменной, то дифференциальное уравнение называют обыкновенным; в противном случае – дифференциальным уравнением в частных производных. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Процесс отыскания решения дифференциального уравнения называется его интегрированием, а график решения дифференциального уравнения – интегральной кривой.
Разностные методы решения дифференциальных уравнений – это способы вычисления значений искомого решения у(х) на некоторой сетке значений аргумента.
Разностные методы позволяют находить только конкретное (частное) решение, например решение задачи Коши. Но эти методы в настоящее время являются основными при решении дифференциальных уравнений с помощью ПК.
О

Рис. 2
дним из простейших разностных методов является метод ломаных или метод Эйлера. Основан на аппроксимации участков траектории на шаге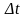 прямыми линиями.
прямыми линиями.
Обладает невысокой точностью, требует малого шага интегтирования.
Если требуется решить задачу Коши на отрезке [х, xn] на данном отрезке выбирают некоторую сетку значений аргумента х0, х1, ..., xn, для которых вычисляют значения функции у по схеме:
yn+1=yn+hnf(xn,yn), hn=xn+xn-1 ,
где n=0,1….N-1.
В
методе Эйлера подынтегральная функция
выносится при нижнем пределе интегрирования:
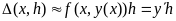 .
Это приближение геометрически
соответствует движению от точки x к
точке х+h по касательной к кривой y(x) в
точке х.
.
Это приближение геометрически
соответствует движению от точки x к
точке х+h по касательной к кривой y(x) в
точке х.
Расчетные формулы метода Эйлера:
yk+1=yk+f(xk,yk)h, xk=xk-1+h,
y(x0)=y0, yk=y(xk).
Этот метод дает хорошее приближение к решению только для достаточно малых h, т.к. погрешность метода Эйлера определяется остаточным членом ряда Тейлора:
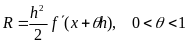
Более высокую точность обеспечивает метод Рунге – Кутта. Наиболее употребительной является следующая схема метода:
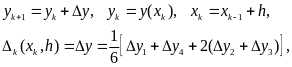
где
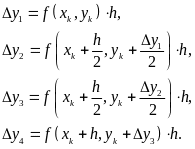
В основе получения вычислительных схем
этого метода лежит разложение функции
y(x) в ряд Тейлора с последующим
преобразованием отрезка ряда к виду,
не содержащему производных. На шаге h
производная
 =
=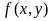 аппроксимируется параболой второго
порядка. Здесь функция f(x,h) определяется
формулой парабол:
аппроксимируется параболой второго
порядка. Здесь функция f(x,h) определяется
формулой парабол:
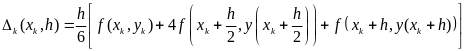 .
.
Если у нас дано дифференциальное
уравнение
=
при начальном условии (хА,уА),
то по известным начальным условиям
(хА,уА) определяется значение
производной в начальной точке А: 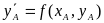 .
.
Из начальной точки А проведится прямая
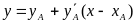 (рис
3) и отмечается значение ее ординаты в
середине шага интегрирования h (т. В) с
координатами
(рис
3) и отмечается значение ее ординаты в
середине шага интегрирования h (т. В) с
координатами
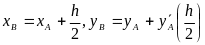 .
.
Н

Рис. 3
аходится значение производной по формуле dy/dx=f(x,y) в точке В: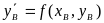 и
проводится из точки А прямую
и
проводится из точки А прямую
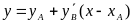 .
Отмечаем значение ординаты этой прямой
в середине шага интегрирования h (точка
С) с координатами
.
Отмечаем значение ординаты этой прямой
в середине шага интегрирования h (точка
С) с координатами
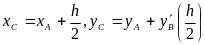 .
.
По уравнению
=
находится значение производной в точке
С:
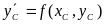 и
проводится из точки А прямая
и
проводится из точки А прямая
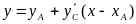 .
Значение ординаты этой прямой в конце
шага интегрирования h (точка D) с
координатами
.
Значение ординаты этой прямой в конце
шага интегрирования h (точка D) с
координатами
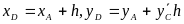 .
.
По уравнению = находится значение производной в точке D:
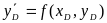 .
.
В результате построений находится
значение производных
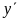 в точках А, В, С и D (рис 4). В точке с
абсциссой
в точках А, В, С и D (рис 4). В точке с
абсциссой
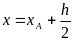 получают два значения производной
вместо одного, что является следствие
приближенности метода. Принимается,
что в этой точке среднее значение
производной:
получают два значения производной
вместо одного, что является следствие
приближенности метода. Принимается,
что в этой точке среднее значение
производной:
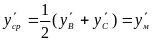 .
.

Рис. 4
Кривая, изображающая зависимость
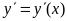 проходит через точки A, M и D, представляет
собой параболу с уравнением:
проходит через точки A, M и D, представляет
собой параболу с уравнением:
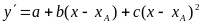 .
.
Значения коэффициентов a, b и с выбираются
из условия прохождения параболы через
точки. Коэффициент
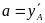 .
Из уравнения параболы
получают систему:
.
Из уравнения параболы
получают систему:
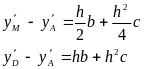
Решением системы является:
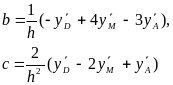
Интегрируя уравнение параболы
в пределах от x=xA до x=xA+h
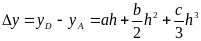 или,
учитывая вышеизложенное:
или,
учитывая вышеизложенное:
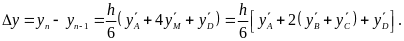
К достоинствам метода Рунге - Кутта следует отнести то, что алгоритмы, полученные на их основе, являются однородными, т.е. не вменяющимися при переходе от одной точки сетки к другой. Кроме того, в методах Рунге - Кутта возможно изменять шаг интегрирования в соответствии с требуемой точностью вычислений без значительного усложнения самого алгоритма. Основным недостатком является то, что для вычисления, приближенного решения в одной точке сетки требуется несколько вычислений правой части уравнения f(x,y). Это приводит, в особенности при сложных правых частях, к значительному увеличению времени вычислений.
Для системы дифференциальных уравнений первого порядка данный алгоритм выполняется для каждого уравнения системы параллельно.
