Решение.

Средняя выработка рабочего рассчитается как:

шт./час.

Обозначим через: - выработку i-го рабочего; - количество рабочих в цехе; - среднюю выработку рабочего. Тогда в общем виде формулу для определения средней выработки можно записать:

.

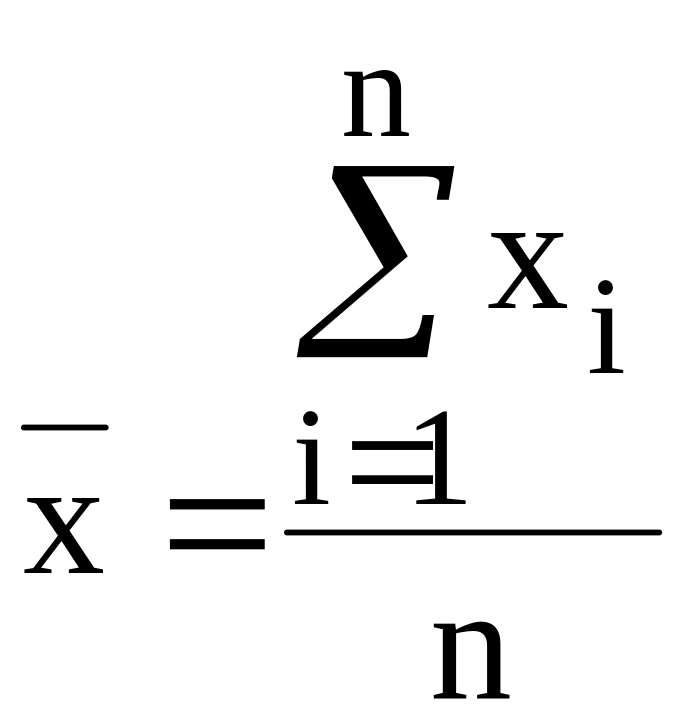Данная формула получила название средней арифметической простой.

Пример 3.2. По сгруппированным данным примера 3.1 определить среднюю выработку рабочего.

Решение.

Сгруппируем данные представленные в таблице примера 3.1. Получим дискретный ряд распределения вида:

Выработка, шт./час	Количество рабочих
6 10 12	1 3 2

Среднюю выработку рабочего рассчитаем как:

шт./час.

Обозначим через: - выработку i-ой группы рабочих; - количество выделенных групп рабочих по выработке; - количество рабочих, относящихся к i-той группе по выработке; - среднюю выработку рабочего. Тогда в общем виде формулу для определения средней выработки можно записать:

.

Данная формула получила название средней арифметической взвешенной, а называется частотой (весом) признака.

Пример 3.3. На основе данных, представленных в таблице примера 3.1, определить средние затраты времени, необходимые для изготовления одной детали (среднюю трудоемкость).

Решение.

Затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной выработке, т.е.:

.

Определим трудоемкость каждого рабочего цеха:

Табельный номер рабочего	Выработка, шт./час	Затраты времени на деталь, час/шт.
1 2 3 4 5 6	12 10 6 10 12 10	1/12 1/10 1/6 1/10 1/12 1/10

Средние затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной средней выработке, т.е.:

час/шт.

Обозначим через: - затраты времени, необходимые для изготовления детали i-тым рабочим; - количество рабочих в цехе; - средние затраты времени, необходимые для изготовления одной детали. Тогда в общем виде формулу для определения средних затрат времени, необходимых для изготовления одной детали, можно записать:

.

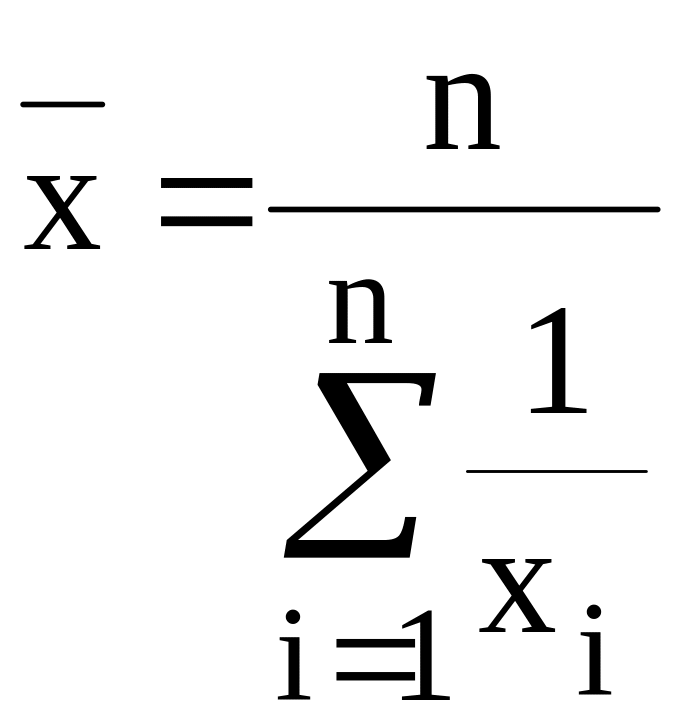Данная формула получила название средней гармонической простой.

Пример 3.4. На основе сгруппированных данных, представленных в таблице примера 3.2, определить средние затраты времени, необходимые для изготовления одной детали (среднюю трудоемкость).

Решение.

Так как затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной выработке, то для каждой группы рабочих по выработке можно определить соответствующую трудоемкость:

Выработка, шт./час	Количество рабочих	Затраты времени на деталь, час/шт.
6 10 12	1 3 2	1/6 1/10 1/12

Средние затраты времени, необходимые для изготовления одной детали, являются величиной обратно пропорциональной средней выработке, т.е.:

час/шт.

Обозначим через: - затраты времени, необходимые для изготовления детали i-ой группой рабочих; - количество выделенных групп рабочих по трудоемкости; - количество рабочих, относящихся к i-той группе по трудоемкости; - средние затраты времени, необходимые для изготовления одной детали. Тогда в общем виде формулу для определения средних затрат времени, необходимых для изготовления одной детали, можно записать:

.

Данная формула получила название средней гармонической взвешенной.

Для определения среднего значения интервального ряда распределения по одной из рассмотренных формул в качестве величины принимается середина соответствующего интервала. Среднее значение интервала рассчитывается по формуле средней арифметической, т.е. как полусумма значений нижней и верхней границ интервала. В случае если ряд распределения имеет первый (последний) открытый интервал, то его необходимо закрыть. Для этого определяют длину последующего (предыдущего) интервала и считают, что закрываемый интервал имеет такую же длину. Тем самым находят нижнюю (верхнюю) границу открытого интервала, т.е. закрывают его.

Выбор той или иной формулы для определения средней величины зависит от экономического смысла усредняемого признака.

Средней арифметической величине присущи следующие математические свойства:

1. произведение средней величины на сумму частот ряда распределения равно сумме произведений каждого значения изучаемого признака на соответствующую ему частоту:

;

2. сумма отклонений каждого значения изучаемого признака от средней величины равна нулю:

;

3. сумма квадратов отклонений каждого значения изучаемого признака от средней величины всегда меньше, чем сумма квадратов их отклонений от любой другой величины:

;

4. уменьшение или увеличение каждого значения изучаемого признака на одну и туже величину приводит к изменению средней на эту величину:

;

5. уменьшение или увеличение каждого значения изучаемого признака в одно и тоже число раза приводит к изменению средней величины в это же число раз:

или ;

6. уменьшение или увеличение частоты каждого значения изучаемого признака в одно и тоже число раз не приводит к изменению средней величины:

.

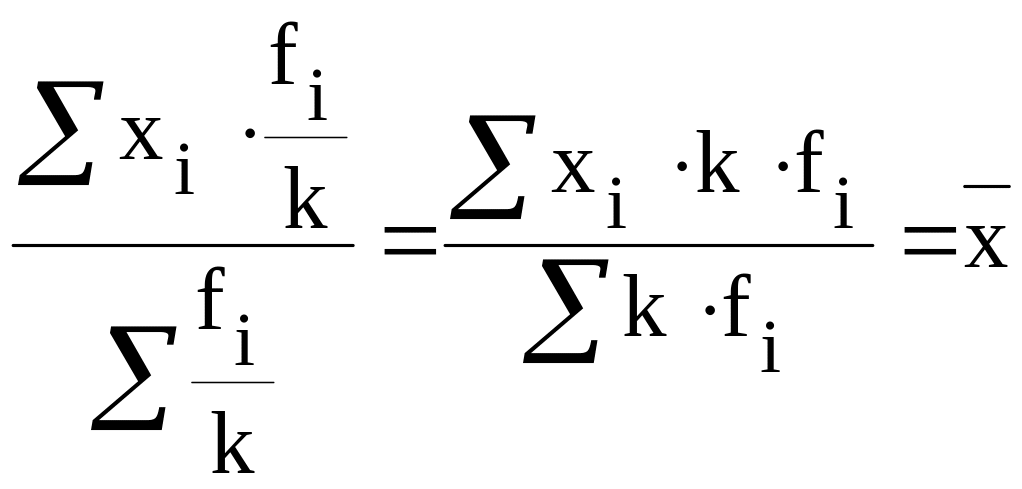Для определения средней арифметической величины часто используется метод моментов (метод отсчета от условного нуля).

В основе этого метода лежат математические свойства средней арифметической, согласно которым, уменьшение (увеличение) всех значений признака на одну и туже величину или уменьшение (увеличение) в одно и тоже число раз, приводит к изменению средней на эту величину или в это же число раз.

Согласно методу моментов среднюю арифметическую рассчитывают по формуле:

,

где - i-тое значение признака или середина i-го интервала;

- значение признака (середина интервала), имеющего наибольшую частоту (условный нуль);

- общий множитель для всех значений признака или их отклонений от условного нуля (для ряда с равными интервалами принимается длина интервала);

- частота i-го значения признака или частное от его сокращения на наибольший общий делитель .

Пример 3.5. По данным о выпуске продукции предприятиями отрасли (столбцы 1 и 2 таблицы) определить по методу моментов среднегодовой объем выпуска продукции.