Тема 8. Статистические методы динамики социально-экономических явлений
Понятие и виды ряда динамики
Основные показатели динамики и способы их расчета
Изучение сезонных колебаний
8.1. Ряд динамики представляет собой совокупность значений, характеризующих изменение изучаемого социально-экономического явления по времени. Любой ряд динамики состоит из двух элементов: временной составляющей и соответствующего значения признака (уровня) ряда динамики.
В зависимости от способа представления уровней различают ряды абсолютных, относительных и средних величин. В зависимости от того представлены ли уровни ряда динамики за определенный период времени или на конкретную дату различают интервальные и моментные ряды. Ряды динамики также бывают с равноотстоящими и неравноотстоящими уровнями.
8.2. Для анализа рядов динамики определяют такие показатели, как абсолютный прирост, темп роста, темп прироста, и абсолютное значение одного процента прироста. Для проведения расчета этих показателей необходимо правильно выбрать базу сравнения. Если каждый уровень ряда динамики сравнивается с предшествующим уровнем, получают цепные показатели, если же каждый уровень ряда динамики сравнивается с одним и тем же уровнем (базой), получают базисные показатели. Выбор той или иной базы сравнения зависит от целей проведения анализа и использования его результатов.
Абсолютный прирост определяют:
для цепных показателей:
;
для базисных показателей:
,
где
- соответственно текущее и предыдущее
значение уровня;
- базисное значение
уровня.
Темп роста определяют:
для цепных показателей:
;
для базисных показателей:
.
Темп прироста определяют:
для цепных показателей:
;
для базисных показателей:
.
Темп прироста для цепных и базисных показателей может также быть определен по формуле:
.
Абсолютное значение одного процента прироста определяется только для цепных показателей по одной из двух формул:
либо
.
В анализе рядов динамики большое внимание следует уделить расчету средних значений показателей динамики.
Выбор формулы для определения среднего значения уровня ряда динамики зависит от его вида:
для интервального ряда с равноотстоящими уровнями среднее значение уровня определяется по формуле средней арифметической простой:
,
где - количество уровней ряда динамики.
для интервального ряда с неравноотстоящими уровнями среднее значение уровня определяется по формуле средней арифметической взвешенной:
,
где
- период
времени, в течение которого значение
уровня не изменяется.
для моментного ряда с равноотстоящими уровнями среднее значение уровня определяется по формуле средней хронологической:
.
для моментного ряда с неравноотстоящими уровнями среднее значение уровня определяется по формуле:
.
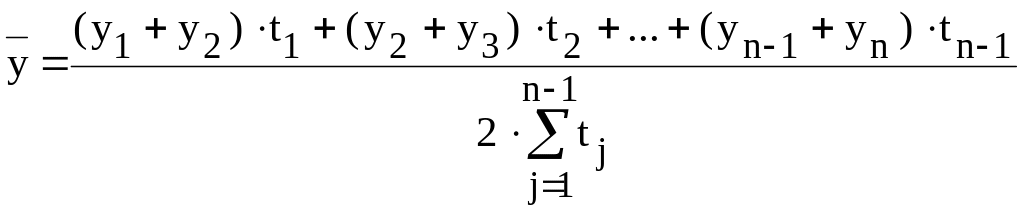Средние значения определяются только для цепных показателей.
Среднее значение абсолютного прироста определяется по одной из двух формул:
либо
,
где - число цепных абсолютных приростов.
Среднее значение темпа роста определяется либо по формуле средней геометрической:
,
где - число цепных темпов роста;
- темпа роста в
долях
либо по формуле:
.
Среднее значение темпа прироста определяется по формуле:
.
Пример 8.1. Произвести анализ динамики производства продукции на коммерческом предприятии за последние 6 лет (исходные данные в 1 и 2 столбцах таблицы). Спрогнозировать объем производства продукции на ближайшие три года, используя модель, построенную на основе среднего темпа роста.