Решение.

Полигон дискретного ряда распределения представлен на графике:

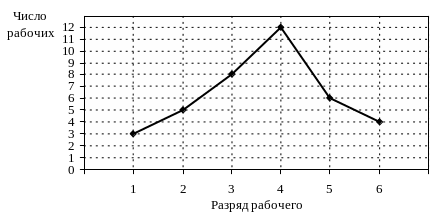
Полигон может быть построен и для интервального ряда распределения, т.е. ряда, у которого группировочный признак задан в виде интервалов. В этом случае по оси абсцисс откладываются средние значения каждого интервала.

Гистограмма − это график, в котором ряд распределения представлен в виде смежных столбцов. Гистограмма обычно используется для графического представления интервального ряда распределения.

Для построения гистограммы на плоскости вычерчивается декартова система координат, по оси абсцисс которой откладываются нижняя и верхняя границы каждого интервала, а по оси ординат − частота или частость. Затем для каждого интервала на уровне соответствующей частоты (частости) на плоскости проводятся горизонтальные отрезки. Опустив из концов отрезков на ось абсцисс перпендикуляры, получаются смежные столбцы. Такой график называется гистограммой ряда распределения.

Пример 6.4. Построить график ряда распределения по следующим данным:

Группы предприятий по среднегодовой стоимости основных средств, млрд.руб.	Число предприятий	Накопленная частота
1 - 2,2	3	3
2,2 - 3,4	9	12
3,4 - 4,6	5	17
4,6 - 5,8	3	20
5,8 - 7	4	24

Решение.

Гистограмма интервального ряда распределения представлена на графике:

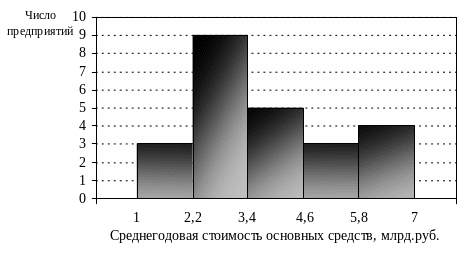
При построении гистограммы для ряда распределения с интервалами неравной длины по оси ординат откладываются значения плотности распределения интервала. Плотность распределения интервала представляет собой отношение частоты (частости) к длине соответствующего интервала:

,

где - частота (частость) интервала;

- длина интервала.

Пример 6.5. Построить график ряда распределения по следующим данным:

Группы предприятий по среднегодовой стоимости основных средств, млрд.руб.	Число предприятий	Плотность распределения
1 - 3 3 - 3,4 3,4 - 4 4 - 6 6 - 7	7 5 3 5 4	3,5 12,5 5 2,5 4

Решение.

Гистограмма интервального ряда распределения с интервалами неравной длины представлена на графике:

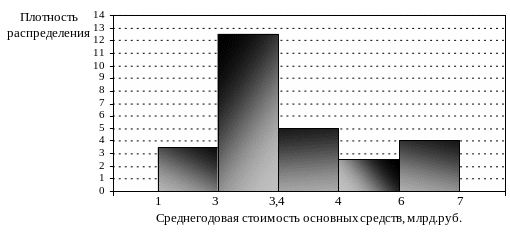
Для графического изображения ряда распределения часто используется кумулятивная кривая распределения. Кумулятивная кривая распределения (кумулята) представляет собой возрастающую ломаную линию. Для построении кумулятивной кривой распределения на плоскости вычерчивается декартова система координат, по оси абсцисс которой откладываются для дискретного ряда распределения значения группировочного признака, а для интервального ряда распределения нижняя и верхняя границы каждого интервала группировки. По оси ординат наносится накопленная частота (частость), представляющая собой суммарное значение частот (частостей) текущего дискретного значения (интервала) группировки и всех предшествующих. Затем для каждого дискретного значения группировочного признака (верхней границы интервала) на уровне соответствующей накопленной частоты (частости) на плоскость наносятся точки. При построении кумуляты интервального ряда распределения выставляется еще одна точка для нижней границы первого интервала на уровне нуля. Соединив точки отрезками, получается ломаная линия. Такой график называется кумулятивной кривой распределения.

Пример 6.6. Построить кумулятивную кривую распределения по данным из примера 6.4.