#45. Тhе apt model.
An asset pricing model based on the idea that an asset's returns can be predicted using the relationship between that same asset and many common risk factors. Created in 1976 by Stephen Ross, this theory predicts a relationship between the returns of a portfolio and the returns of a single asset through a linear combination of many independent macro-economic variables.
Risky
asset returns are said to follow a factor
structure if
they can be expressed
as:
,
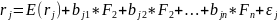where
E(rj) is the jth asset's expected return,
Fk is a systematic factor (assumed to have mean zero),
bjk is the sensitivity of the jth asset to factor k, also called factor loading,
and εj is the risky asset's idiosyncratic random shock with mean zero.