#18. What is rss, ess, tss?
In statistics, the residual sum of squares (RSS) is the sum of squares of residuals. .
In
a model with a single explanatory variable, RSS is given by
,
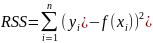where yi is
the i th value
of the variable to be predicted, xi is
the i th value
of the explanatory variable, and f(xi) is
the predicted value of yi.
In a standard linear simple regression model,
,
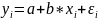where a and b are coefficients, y and x are
the regressand and
the regressor,
respectively, and ε
is the error term. The sum of squares of residuals is the sum
of squares of estimates of εi;
that is
,
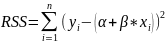where α is
the estimated value of the constant term a and β is
the estimated value of the slope coefficient b.
Note that RSS is effectively a quadratic expression in B1 and B2,
with numerical coefficients determined by the data on X and Y in the
sample.
The explained sum of squares (ESS) is the sum of the squares of the deviations of the predicted values from the mean value of a response variable, in a standard regression model — for example, yi = a + b1x1i + b2x2i + ... + εi, where yi is the i th observation of the response variable, xji is the i thobservation of the j th explanatory variable, a and bi are coefficients, i indexes the observations from 1 to n, and εi is the i th value of the error term. In general, the greater the ESS, the better the estimated model performs.
If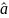 
and
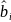are
the estimated coefficients,
then
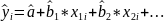is the i th predicted
value of the response variable. The ESS is the sum of the squares of
the differences of the predicted values and the mean value of the
response variable:
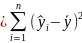. In general: total
sum of squares = explained
sum of squares + residual
sum of squares.
In statistical
data analysis the total
sum of squares (TSS)
is a quantity that appears as part of a standard way of presenting
results of such analyses. It is defined as being the sum, over all
observations, of the differences of each observation from the
overall mean.
In statistical linear
models, (particularly in standard regression
models), the TSS is
the sum of
the squares of
the difference of the dependent variable and its grand
mean:
.
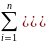For wide classes of linear models: Total sum of squares = explained
sum of squares + residual
sum of squares.
Also for all RSS, ESS, TSS there is an explanation for OLS (ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model), which is extremely big and can’t be presented within an hour.
#19. The normal equations for the regression coefficients.
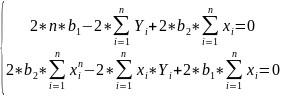
These equations are known as NORMAL EQUATIONS for the regression coefficients.
Далее следует сраный вывод на страницу.
;
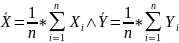
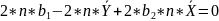
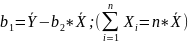
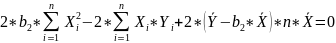
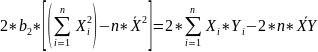
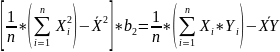
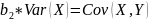
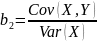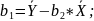
Все, хватит.
#20. Formulas for estimates b1 and b2.
The same as #19.
#21. Least Squares Regression.
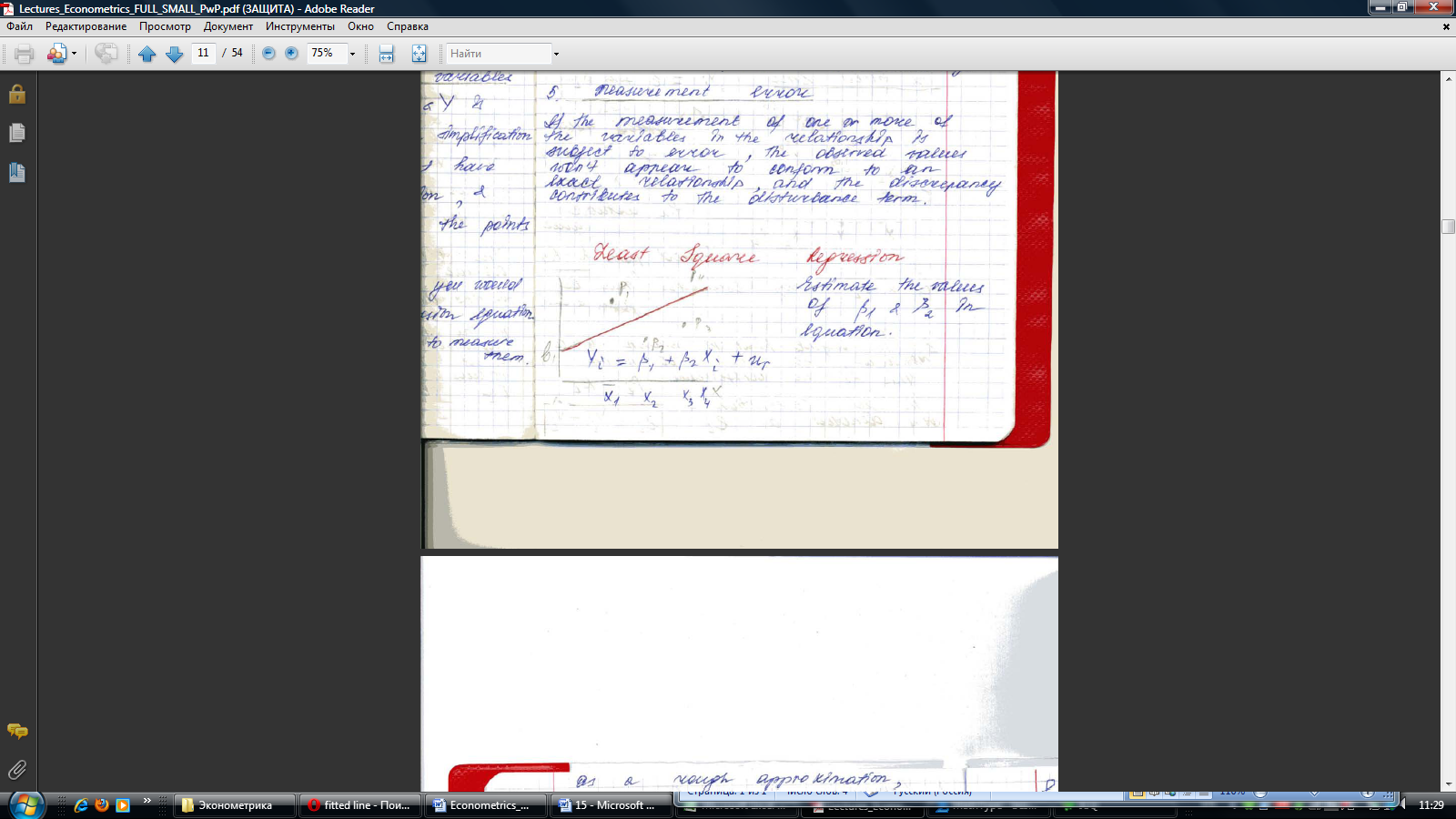
Estimate the values of ß1 and ß2 in equation. As a rough approximation, plot 4 P points and draw a line. The intersection of line with Y-axis provides an estimate of the intercept ß1, which is denoted by b1. And the slope provides an estimate of the slope coefficient ß2 which will be denoted as b2.
#22. Interpretation of a Regression Equation.
A foolproof way of interpreting the coefficients of linear regression Yi=b1+b2Xi, when X and Y are variables with straightforward natural units (not logarithms or other functions)
1. one-unit increase in X will cause a b2 ↑ in Y
2. To check what units of X and Y are, and to replace the word “unit” with the actual unit of measurement.
3. Whether the result could be expressed in a better way, without altering its substance.
4. The constant b1 gives the predicted value of Y for Y equal to 0. It may have a plausible meaning depending on the context.
#23. Goodness of Fit: R2.
Three useful results relating to OLS regression.
1)Ei=Yi-Ŷi=Yi-b1-b2Xi
ei=
Yi-nb1-b2
Xi|:n
Ē=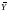
-b1-b2
=
-(
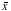-b2
)-b2
=0
B1= -b2
2)ei=Yi- Ŷi ei= Yi
3)cov(Ŷ,e)=cov(b1+b2X,
e)=
cov(b1,e)+cov(b2x,e)=b2cov(x,e)=b2cov(x,Y-b1-b2x)=b2[cov(X,Y)-cov(X,b1)-b2cov(X,X)]=b2[cov(X,Y)-b2varX]=b2[cov(X;Y)-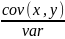
varx]=0
Split Yi in each observation in 2 components: Ŷi and ei. After running a regression Yi=Ŷi+ei
VarY=Var(Ŷ+e)=var(Ŷ)+var e+2 cov (Ŷ,e)
cov (Ŷ,e) must be equal to 0 VarY=var Ŷ +var e
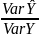is
a proportion of var explained by the regression line.
The proportion is known as the coefficients of determination of R2
R2=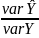
.
The max of R2
=1
This
occurs when the regression line fits the observations exactly, to
that
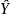i=Yi
in all observations and all the residuals are 0. Var Ŷ=Var Y, var
e=0
If there is no apparent relationship between the values of Y and X in the sample, R2 will be close to 0.
#24. The F-Test of Goodness of Fit.
Even if there is no relationship between Y and X, in any given sample of observations there may appear to be one, if only a faint one.
Only by coincidence will the sample Cov=0.
Accordingly, only by coincidence the correlation coefficient and R2 will be equal to 0.
Suppose, that the regression model is
Yi=ß1(real intercept)+ß2(slope )Xi(value)-Ui(disturbance term)
We take as our null hypothesis that there is no relationship between Y and X, that is
H0: ß2=0
The value would be exceeded by R2 by chance, 5%of time
This figure is a critical level of R2 for a 5%significance test.
If it is exceeded, we reject the null hypothesis
H1:
ß2
0
Suppose, you can decompose the variance of the dependent variable into “explained” and “unexplained” components using the formula var(Y)=varŶ+var(e)
(Yi-
)2
=
(Ŷi-
)2
+
e2i
E=0, sample mean of Ŷ= sample mean of Y
The F statistic for the goodness of fit of a regression is written as the explained sum of squares per explanatory variable, divided by the residual sum of squares per degree of freedom remaining:
F=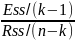
k-number of parameters
k-a-slope coefficients
F=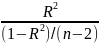
If F>Fcrit. Than the “explanation” of Y is better than is likely to have arisen by chance.
Fcrit.=FРаспобр(
;
;
)
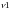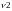=0,05, =n-k, =k