§5. Функциональные ряды. Определение. Понятие равномерной сходимости.

Функциональным называется ряд, членами которого являются функции, например одной переменной .

Общий вид:

где

Рассматривать ООФ функции можно на или .

Примеры функциональных рядов:

1) - степенной ряд

2) - пример тригонометрического ряда

3)

4)

Точка сходимости функционального ряда - это такое числовое значение , при котором числовой ряд является сходящимся.

Точка расходимости функционального ряда - это такое числовое значение , при котором числовой ряд является расходящимся.

Область сходимости функционального ряда – это множество всех его точек сходимости.

Область расходимости функционального ряда – это множество всех его точек расходимости.

Пример:

- точка сходимости, так как очевидно сходится.

- точка сходимости, так как - сходится абсолютно.

…

- область сходимости данного ряда

- область расходимости.

Сумма функционального ряда:

Рассмотрим функциональный ряд в области его сходимости:

области сходимости ряда сумма ряда

области сходимости ряда, так что области сходимости.

Пример:

, т.е. функция может быть представлена сходящимся степенным рядом.

Связь суммы функционального ряда с его частичной суммой:

Рассмотрим сходящийся функциональный ряд:

- п-я частичная сумма ряда,

- п-ый частичный остаток

области сходимости

области сходимости

с погрешностью , при этом определить количество членов ряда n придется различным способом для различных х.

Понятие о равномерной сходимости функционального ряда.

Если функциональный ряд сходится для , то для

для причем номер зависит не только от , но и, вообще говоря, зависит от

Если для некоторой части множества можно указать в этом определении номер одинаковый для всех , то говорят, что функциональный ряд при сходится равномерно к функции .

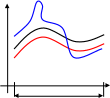
Иллюстрация к понятию равномерной сходимости

у

0 х

Х

, но для различных , т.е. равномерной сходимости нет.

у

-коридор функции ,

х

Х

X’

при , причем можно указать одинаковыми , т.е. присутствует равномерная сходимость.

Равномерно сходящиеся функциональные ряды обладают особыми свойствами, а именно только для них выполняются операции

1. Предельный переход

2. Интегрирование

3. Дифференцирование

и т.д.

Список основных свойств равномерно сходящихся рядов

Если функциональный ряд сходится к функции равномерно при , то

1. Сумма ряда является непрерывной функцией

2. Функциональный ряд можно почленно интегрировать, в результате получается ряд с суммой, равной интегралу от суммы исходного ряда

3. Если ряд сходится равномерно для , то исходный функциональный ряд можно почленно дифференцировать,т.е.

На практике для определения равномерной сходимости рядов применяется достаточный признак Вейерштрасса:

Если для функционального ряда , можно указать знакоположительный числовой сходящийся ряд , такой, что выполняется неравенство , то функциональный ряд на множестве Х сходится равномерно.

При этом числовой ряд называется мажорантой для функционального ряда , а функциональный ряд называется мажорируемым.

Краткая формулировка признака Вейерштрасса:

Если функциональный ряд является мажорируемым на некотором множестве, то он сходится равномерно на этом множестве.

Для мажорируемых рядов есть еще термин правильно сходящиеся ряды.

Пример:

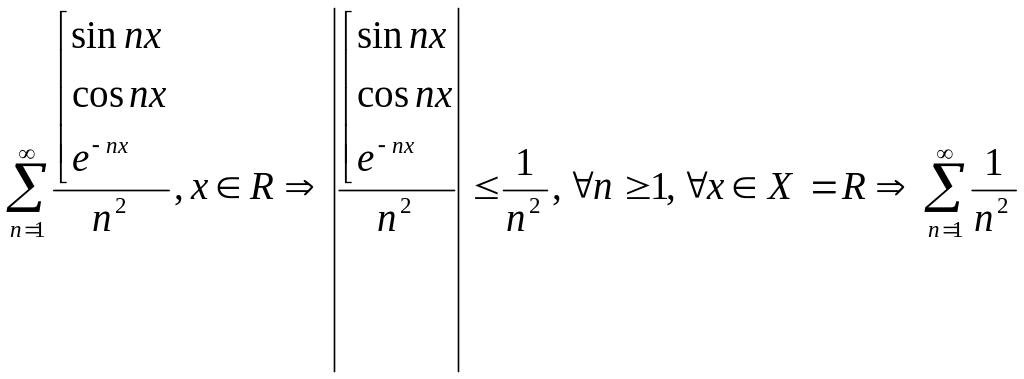является мажорантой для данных функциональных рядов данные функциональные ряды сходятся равномерно .