3. - Знакопеременный ряд;

исследуем сходимость соответствующего ряда из модулей:

этот знакоположительный ряд сходится по признаку сравнения, так как

и ряд сходящийся;

по признаку абсолютной сходимости заключаем, что исходный ряд так же является сходящимся.

На основании определения абсолютной сходимости делаем вывод, что знакопеременный ряд сходится абсолютно.

Упражнения для самостоятельной работы

Задача 1

Исследуйте на сходимость следующие знакопеременные ряды, используя достаточный признак абсолютной сходимости:

1) 2) 3) 4)

5)

Задача 2

Исследуйте на сходимость для следующих знакочередующиеся ряды по признаку Лейбница:

1) 2) 3) 4) 5)

Задача 3

Исследуйте тип сходимости (абсолютная или условная) для следующих знакопеременных рядов:

1) 2) 3)

4) 5)

Ответы к упражнениям для самостоятельной работы

Задача 1

1) и 2) – сходятся; 3),4),5) – ответ дать нельзя.

Задача 2

1), 2), 3), 4) – сходятся; 5) – ответ дать нельзя.

Задача 3

1), 2), 3) – сходятся абсолютно; 4),5) – сходятся условно.

§4. Основные свойства числовых рядов. Приближенное вычисление суммы числового ряда

Запишем основные сведения о числовых рядах:

- ₍₁₎

- это n-я частичная сумма ряда,

- это n-й частичный остаток ряда.

Числовой ряд (1)

_{Число S называется суммой сходящегося ряда, это отражается равенством}

_{Очевидно, что любой ряд можно записать сложением его частичной суммы и соответствующего остатка :}

_;

_{Поэтому для сходящегося ряда верно, что так как}

Основные свойства числовых рядов

Можно доказать справедливость следующих фактов.

1. О связи сходимости ряда со сходимостью его остатка

Если числовой ряд сходится, то сходится и любой его остаток; для расходящегося числового ряда расходится и любой его остаток.

Следствие: сходимость числового ряда не нарушается, если отбросить или добавить конечное число его первых членов.

2. Об умножении ряда на число

Сходимость ряда не нарушается, если все его члены умножить на одно и то же число, не равное нулю.

Следствие: общий множитель всех членов ряда можно выносить за знак суммы:

, то есть свойство дистрибутивности умножения относительно сложения остается справедливым и для бесконечных сумм.

3. О сложении числовых рядов

Два сходящихся ряда можно почленно складывать, при этом складываются и суммы этих рядов, т.е. если то

Замечание: если хотя бы один из складываемых рядов является расходящимся, то в результате сложения получится также расходящийся ряд.

4. О перестановке членов числового ряда

Если числовой ряд сходится абсолютно, то его члены можно переставлять произвольным образом, при этом абсолютная сходимость и сумма ряда не изменится.

Для абсолютно сходящихся рядов выполняется обратная операция деления ряда на ряд.

Если числовой ряд сходится условно, то его члены можно представить так, что его сумма станет равной любому наперед задуманному или даже равной .

Следовательно, в условно сходящихся рядах представлять слагаемые нельзя, так как в результате может измениться сумма ряда или даже ряд станет расходящимся.

Например, рассмотрим ряд Лейбница, который условно сходится:

операцию вычитания рядов выполнять нельзя, так как оба ряда расходятся.

На основании этого свойства о перестановке членов числового ряда абсолютную сходимость рядов называют сильной сходимостью, так как она обусловлена именно малостью членов ряда при больших n, а не чередованием их знаков;

При этом условную сходимость нужно назвать слабой и работать с условно сходящимися рядами нужно осторожно.

условная сходимость рядов называется слабой сходимостью (абсолютная сходимость – сильной)

работать с условно сходящимся рядами нужно очень осторожно.

5. О перемножении рядов

Абсолютно сходящиеся ряды можно перемножать аналогично конечным суммам: каждый член одного ряда умножается на каждый член другого ряда.

то есть в результате перемножения двух рядов получается двойной ряд.

Например,

Оценки остатков некоторых сходящихся рядов. Приближенное вычисление суммы ряда

Рассмотрим сходящийся числовой ряд:

Так как и то при достаточно больших номерах n значения частичных сумм становится сколь угодно близкими к сумме ряда S , а значения соответствующих частичных остатков сколь угодно близкими к нулю. На основании этго можно вычислять приближенное значение суммы ряда S:

, погрешность этого приближенного равенства равна , она уменьшается с увеличением .

Задача «Вычислить сумму сходящегося числового ряда приближенно с наперед заданной точностью означает, что сумму ряда нужно заменить такой частичной суммой , чтобы соответствующий отбрасываемый остаток удовлетворял условию :

с точностью , если (2)

Для практической работы по приближенной формуле (2) нужно иметь оценки для остатков сходящихся рядов.

Оценки остатков некоторых рядов

1)	Если знакочередующийся ряд сходится по признаку Лейбница, то модуль его остатка имеет оценку:

Для доказательства запишем знакочередующийся ряд в равернутом виде и выделим в нем частичный остаток :

запишем иначе:

так как ряд удовлетворяет условиям Лейбница, то , поэтому все внутренние скобки положительны, следовательно, при отбрасывании этих положительных скобок получим искомую оценку:

Примеры:

Вычислим приближенное значение суммы S каждого из следующих рядов с точностью :

1) - ряд Лейбница, сходится условно;

, где нужно взять таким, чтобы соответствующий остаток . Так как ряд удовлетворяет признаку сходимости Лейбница, то

нужно взять

Ответ: или

2) - знакочередующийся ряд, удовлетворяет условиям признака Лейбница.

Таким образом

Ответ: . Заметим, что ряд сходится быстрее, чем ряд , то есть для того, что бы получить приближенное значения сумм этих рядов с одинаковой точностью, у первого ряда нужно взять меньше слагаемых, чем во втором.

2)	Если знакоположительный ряд сходится по интегральному признаку Коши, то есть сходится , где , то его остаток имеет следующую оценку: .

Пример

Вычислим приближенно с точностью сумму ряда из обратных квадратов

- сходится по интегральному признаку Коши.

вычислить с точностью , при этом

нужно взять тогда с точностью

Ответ:

_{Заметим, что знакоположительный ряд из обратных квадратов сходится значительно медленнее, чем соответствующий знакочередующийся ряд} .

3333)

Если знакоположительный ряд сходится к признаку Даламбера, т.е. то его остаток имеет следующую оценку .

Пример

- геометрический ряд со знаменателем 0,7, сходится по признаку Даламбера, так как

Вычислим с точностью

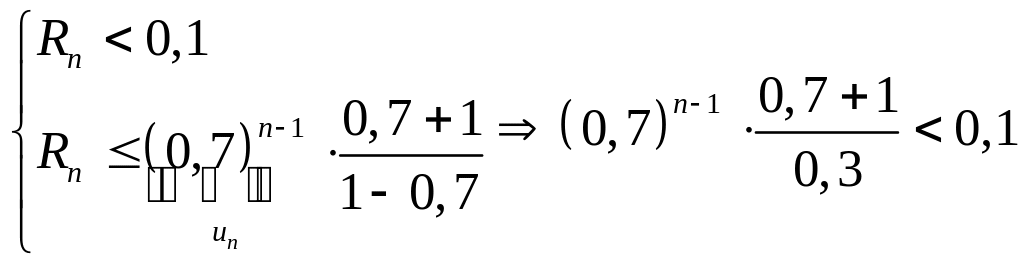
_Ответ:

_{Замечание}

1.При приближенном вычислении значения суммы ряда не нужно бояться взять лишние слагаемые в частичную сумму

2.При вычислении слагаемых в также возможны приближенные значения слагаемых; их нужно брать с большей точностью, чем вычисляется сумма ряда S (то есть нужно брать «запасные цифры после запятой»).

_{Упражнения для самостоятельной работы}

_{Задача 1}

_{Даны несколько сходящихся числовых рядов:}

1) (геометрический ряд);

2) (знакочередующийся геометрический ряд);

3) (ряд из обратных факториалов);

4) (знакочередующийся ряд из обратных факториалов);

5) (ряд Дирихле);

6) (знакочередующийся ряд Дирихле).

_{Выведите формулы для оценки остатка каждого из этих рядов.}

_{Ответы к упражнениям для самостоятельной работы}

_{Задача 1}