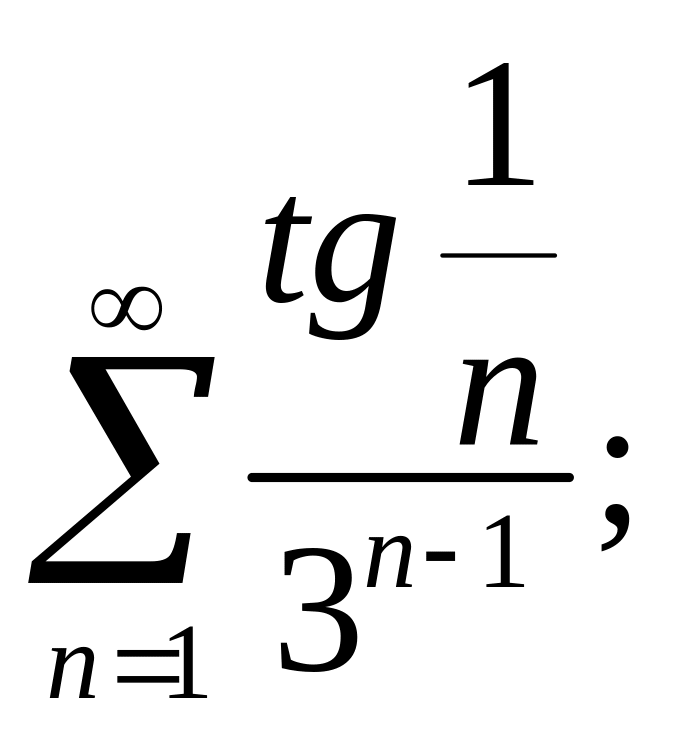1. Гармонический ряд:

Рассмотрим несобственный интеграл:

несобственный интеграл расходится, следовательно, расходится и гармонический ряд;

2. ряд из обратных квадратов:

- непрерывная и монотонно убывающая функция при

несобственный интеграл сходится, следовательно, ряд из обратных квадратов также сходится.

3. - обобщенный гармонический ряд (ряд Дирихле)

Очевидно, что при p<0 члены данного ряда монотонно возрастают, а при p=0 остаются все равными 1, поэтому при , следовательно, ряд Дирихле расходится, так как для него не выполняется необходимое условие сходимости.

Далее рассматриваем случаи , для них необходимое условие сходимости выполняется ( ), поэтому ряд может сходиться;

вводим функцию - непрерывную и монотонно убывающую при и рассматриваем от неё несобственный интеграл:

на основании интегрального признака Коши заключаем, что ряд Дирихле сходится при и расходится при .

Для ответа собираем все случаи проведенного исследования:

обобщенный гармонический ряд

_{При практическом исследовании числовых рядов на сходимость}

_{рекомендуется проводить работу по следующей схеме:}

- указать тип ряда _;

- проверить необходимое условие

если условие

- для ряда, который может сходиться, подбирать достаточное условие в соответствии с типом ряда; обычно ответ можно получить по нескольким достаточным признакам;

применять достаточное признаки можно перебором до получения ответа.

_{Примеры:}

1. - знакоположительный ряд;

необходимое условие:

ряд может сходиться.

Покажем, что сходимость данного ряда может быть получена по нескольким достаточным признакам.

Признак Даламбера:

Признак сравнения в непредельной форме:

Ряд сходится, так как это обобщенный гармонический ряд с , следовательно исходный ряд сходится по признаку сравнения в непредельной форме.

2. - ряд знакоположительный;

необходимый признак сходимости:

ряд может сходиться.

Покажем, что для данного ряда ответ о сходимости можно получить по признаку сравнения в предельной форме или по интегральному признаку Коши, а по признаку Даламбера получить ответ нельзя.

Признак сравнения в предельной форме:

выберем для сравнения гармонический ряд , расходимость которого известна, и вычислим предел отношения членов обоих рядов:

данный ряд так же расходится как и гармонический ряд.

Интегральный признак Коши:

несобственный интеграл расходится, следовательно, расходится и ряд.

Признак Даламбера:

ответ о сходимости исследуемого ряда по признаку Даламбера дать нельзя.

Упражнения для самостоятельной работы

Задача 1

Исследуйте сходимость следующих знакоположительных рядов, используя необходимый и один из достаточных признаков сходимости:

1)	2)	3)
4)	5)	6)
7)	8)	9)
10)	11)

Ответы к упражнениям для самостоятельной работы

Задача 1

1)сходится (по признакам сравнения);

2)сходится (по признаку Даламбера);

3)расходится (по признакам сравнения);

4)расходится (по признакам сравнения или по интегральному признаку Коши);

5)сходится (по признаку Даламбера);

6)сходится (по радикальному признаку Коши);

7)расходится (т.к. не выполняется необходимое условие сходимости);

8)расходится (т.к. не выполняется необходимое условие сходимости);

9)расходится (по признакам сравнения или по интегральному признаку Коши);

10)расходится (по интегральному признаку Коши);

11)сходится (по интегральному признаку Коши).