Оглавление

Тема 1. Числовые и степенные ряды. 1

§1. Числовые ряды. Определение. Сходимость. Расходимость. Необходимый признак сходимости. 1

§2. Достаточные признаки сходимости знакоположительных рядов. 8

§3. Достаточные признаки сходимости знакопеременных рядов. Абсолютная и условная сходимости 19

§4. Основные свойства числовых рядов. Приближенное вычисление суммы числового ряда 24

§5. Функциональные ряды. Определение. Понятие равномерной сходимости. 31

§6. Степенные ряды. Теорема Абеля. Область сходимости. Радиус сходимости. 35

§7. Ряды Тейлора и Маклорена. 40

§8. Основные приложения степенных рядов 46

Тема 1. Числовые и степенные ряды. §1. Числовые ряды. Определение. Сходимость. Расходимость. Необходимый признак сходимости.

Ряд – это сумма бесконечного количества слагаемых

Числовой ряд – это сумма бесконечного количества слагаемых, являющихся числами.

  (1)

- общий член ряда

Примеры:

1. 1+1+…+1+…

2. 

(геометрический ряд со знаменателем q)

3. (гармонический ряд)

4. (знакочередующийся ряд)

5. (знакопеременный ряд)

n-я частичная сумма ряда (1) – это сумма первых его n слагаемых, то есть:

последовательность частичных сумм :

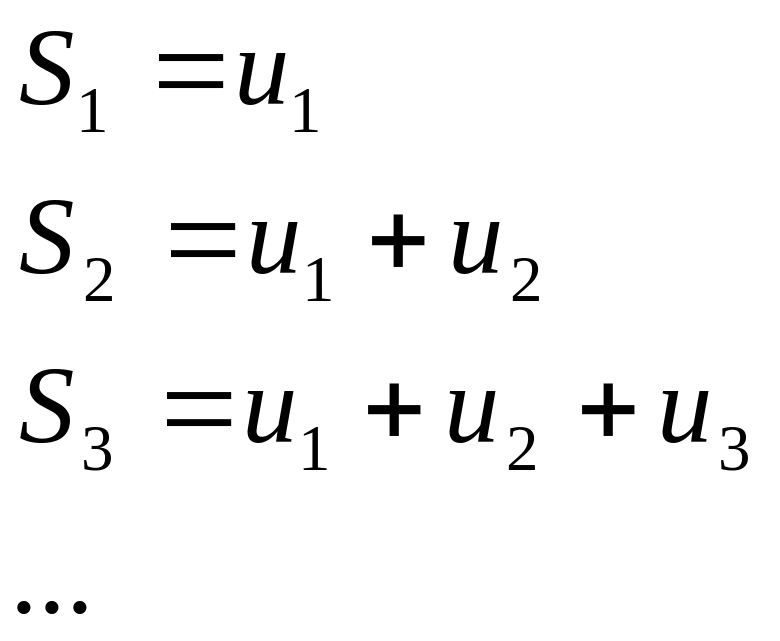
Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм; в противном случае ряд (1) называется расходящимся.

Если , то ряд является сходящимся, при этом число S называется суммой ряда.

Если , то ряд является расходящимся и суммы не имеет.

Примеры:

1. =

ряд сходится и его сумма равна 2, то есть .

Аналогично для любого геометрического ряда с :

,

2. =

расходится и суммы не имеет.

Аналогично для любого геометрического ряда с :

,

3. 

ряд расходится

4. =

ряд расходится.

5. 

можно сделать предположение, что

Докажем это предположение методом математической индукции:

1. если n=1, то

2. пусть верно, что ,

вычислим =

на основании метода математической индукции заключаем, что формула верна при _.

Вычисляем ряд сходится и его сумма равна 1.

6. 

Прежде, чем вычислять , разложим рациональную дробь на простейшие дроби:

при

_{Теперь вычисляем частичные суммы данного ряда:}

n-ый частичный остаток ряда (1) – это ряд, который получается из ряда (1) отбрасыванием первых n слагаемых, то есть:

_{Очевидно, что ряд (1) можно представить сложением его n-й частичной суммы и n-го частичного остатка:}

Если ряд сходится, то при _{, где S – это сумма ряда; при этом очевидно, что при ;}

_{поэтому} и погрешность этого равенства, равная уменьшается с увеличением n.

Отсюда следует, что сумма сходящегося ряда S может быть вычислена приближенно с любой наперед заданной точностью , для этого нужно только уметь получить оценку для остатка ряда :

с точностью , если .

Сходимость и расходимость числовых рядов устанавливается на практике с помощью необходимого и достаточных признаков.

Необходимый признак сходимости любых рядов:

Если ряд сходится, то предел его общего члена равен нулю: .

Пусть ряд сходится ; это означает, что существует конечный предел последовательности его частичных сумм, то есть существует:

, где .

Тогда очевидно, что , где , так как -это последовательность тех же частичных сумм ряда с запаздывающим индексом на единицу.

Используя частичные суммы и , можно записать общий член ряда :

, можно записать общий член ряда :

Заметим, что ряд с общим членом, не стремящимся к нулю, сходиться не может.

Потому, начиная исследовать любой числовой ряд по необходимому признаку сходимости, можем получить один из следующих двух результатов:

Примеры:

1) -ряд расходится, так как сходиться не может, потому что если предположить сходимость, то получаем противоречие с необходимым условием;

2) - ряд может сходиться, так как , то есть необходимое условие сходимости выполнено;

3) -ряд расходится, так как , то есть ряд расходится потому, что не выполняются необходимые условия сходимости.

Замечание.

Если члены ряда могут быть как положительными, так и отрицательными, то при проверке необходимого условия сходимости вычисляют предел общего члена ряда, взятого по модулю:

, так как в случае будет и .

Из доказательства необходимого признака сходимости рядов не следует, что этот признак является также и достаточным. В подтверждение его недостаточности можно привести пример гармонического ряда

,

Который расходится, хотя необходимый признак сходимости для него выполняется.

Доказательство расходимости гармонического ряда можно провести следующим образом. Напишем подробнее гармонический ряд:

(*)

Теперь составим вспомогательный ряд, который будет отличаться от гармонического ряда тем, что в каждой скобке выражения (*) все слагаемые будут заменены на меньшее из них:

(**)

Так как каждый член гармонического ряда (*) больше или равен члену с таким же номером составленного ряда (**), то для их частичных сумм и верно неравенство:

при .

Частичные суммы ряда (**) легко вычисляются при :

Таким образом показано, что частичные суммы составленного ряда (**) при достаточно больших k становятся сколь угодно большими; это обозначает, что . Но тогда , так как . Теперь на основании определения расходящегося ряда заключаем, что гармонический ряд расходится.

Упражнения для самостоятельной работы

Задача 1

Даны числовые ряды:

1)

2) ;

3) ;

Составьте выражение для n-й частичной суммы каждого ряда, вычислите и сделайте вывод о сходимости или расходимости данного ряда; в случае сходимости запишите сумму ряда.

Задача 2

Составьте общий член каждого из следующих рядов, вычислите и проведите исследование сходимости/расходимости рядов по необходимому принципу сходимости:

1) ;

2) ;

3) ;

4) ;

5) .

Ответы к упражнениям для самостоятельной работы

Задача 1

1) , , ряд сходится и его сумма S= ;

2) , , ряд расходится;

3) , , ряд сходится и его сумма S= .

Задача 2

1) , , ряд может сходиться;

2) , , ряд может сходиться;

3) , , ряд расходится;

4) , , ряд может сходиться;

5) , , ряд расходится.