Глава 2 Место точки на меридианном эллипсе

в системе прямоугольных координат

2.1 Связь прямоугольных координат с географическими

Прямоугольные координаты x и y применяются в картографии и геодезии при расчетах для построения рамок карт в различной проекции. Найдем эти координаты в зависимости от широты и параметров эллипса а и b.

Из канонического уравнения меридианного эллипса имеем:

(1.4)

После дифференцирования этого уравнения получим

и

Из рисунка (Рис.1.5) тангенс угла, составленного касательной с осью х, равен производной

, откуда = tg(90-) = - ctg и , а

Подставляя значение y в основное уравнение эллипса, получим:

= 1

После преобразования и, учитывая, что меридианный эллипс характеризуется эксцентриситетом (е) как:

, получим значение прямоугольной координаты х:

(1.5)

К

ds

dx

dy

Рис.1.5

Теперь подставив в (1) значение х после преобразования получим:

(1.6)

2.2 Главные радиусы кривизны сечения меридианного эллипса

Зная значения координат точки на меридианном эллипсе в прямоугольной системе, определим значения главных радиусов кривизны меридианного сечения М и нормального к нему сечения N. Кривизна любой кривой определяется соотношением:

М =   (1.7)

Из треугольника АВС, приведенного на Рис.1.4, имеем:

ds = - , знак (-) говорит о том, что с увеличением широты () радиус (r) уменьшается.

Тогда: М =   = , но dr = dx, тогда

М = получим, если продифференцируем значение х в прямоугольных координатах (1.5).

, после преобразования получим:

(1.8)

Здесь:  - географическая широта

а – большая полуось Эллипсоида Красовского, а = 6378245м

е² – квадрат первого эксцентриситета е² = 0,0066934

Нормальный радиус эллипса (N) зависит от координаты х как

N = , после подстановки выражения х получим:

(1.9)

и

Где М – меридианный радиус кривизны,

N- нормальный радиус кривизны,

R – средний радиус кривизны.

2.3 Длина одной минуты дуги меридиана.

Длина S одной минуты дуги меридиана может быть определена из следующего равенства:

d S = M d = (1.10),

следовательно, дуга меридиана между параллелями ₁ и ₂ будет:

S = a(1-e²)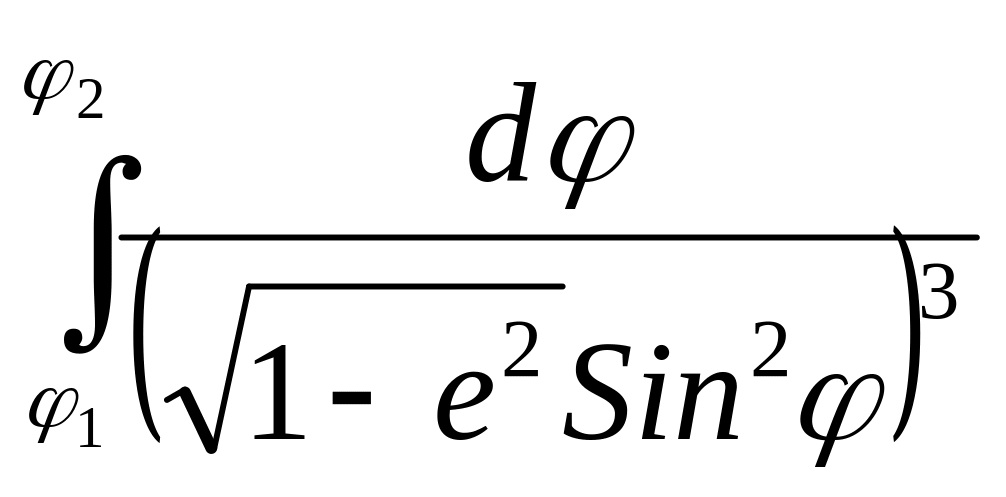 (1.11)

Этот интеграл не выражается в элементарных функциях, поэтому подынтегральное

выражение разложим в ряд, получим:

= 1 + 3/2e²Sin² + 15/8e⁴ Sin⁴ + 105/48e⁶Sin⁶ + ……..

Продолжим разложение значений Sin.

Sin² = ½ - 1/2Cos2 - …………..

Sin⁴ = 3/8 – 1/2Cos2 + 1/8 Cos4 + ………….тогда:

= A – B Cos2 + C Cos4 - Dcos6 +……, теперь находим значения коэффициентов А, В.

А = 1 + 3/4е² + 45/64е⁴ + 175/256е⁶ + …………..

В = 3/4е² + 15/16е⁴ + 525/512е⁶ + ……….Подставляя эти значения коэффициентов в знаменатель формулы (1.11) и, принимая d = arc1^ , получим следующее выражение длины одной минуты дуги меридиана:

S = a(1-e²) A arc1 - a(1-e²) B arc1 Cos2.

Подставляя значения параметров эллипсоида Красовского а и е²:

а(1-е²) А = 6 368 027,5

а(1-е²) В = 32 073 и значение d = arc1 =

получим окончательно:

S = 1852,25 – 9,31 Cos2 метры (1.12)

Как видим, длина одной минуты дуги меридиана величина переменная, зависит от удвоенной широты места исследуемой точки и меняется в пределах от 1843,0 м на экваторе и до 1861,6 м на полюсе.

В навигации принято Землю принимать за шар, у которого длина одной минуты дуги меридиана равна округленной до целого значения величины 1852 метра.

Эту величину морской мили в метрах узаконили на Международном гидрографическом бюро в Монако в 1928 году.