6.4 Аналитическое счисление

Аналитический способ счисления (его еще называют письменным счислением) применяется в тех случаях, когда графическое счисление невозможно или когда оно сопровождается значительными графическими погрешностями.

Формулы аналитического счисления являются основой алгоритмов автоматизированного счисления.

Аналитическим счислением называется вычисление приращений к исходным координатам, обусловленным движением судна, с помощью которых определяются счислимые координаты на заданный момент времени. Аналитическое счисление применяется при плавании вдали от берегов, использовании мелкомасштабных навигационных карт, расчетах счислимых широты и долготы при решении астрономических задач и, наконец, формулы аналитического счисления заложены во все автоматические счислители координат и путепрокладчики.

Судно находится в точке А с координатами (₁ ₁) и следует постоянным курсом по локсодромии в точку пришествия В с координатами (₂ ₂) (Рис.1.38а).

P_N a¹ d

b¹

РД B b)

а) d

a¹ b¹ К ds

К S

A dS A

РД Рис.1.38

Если будут известны сделанные судном разность широт (РШ) и разность долгот (РД), то координаты точки пришествия В можно получить из выражений:

₂ = ₁ + РШ и ₂ = ₁ + РД

Значения разности широт и разности долгот вычислим по элементам движения судна:

- курса (К) и

- пройденного расстояния (S).

Обратимся к элементарному треугольнику А а¹ b¹ (Рис.1.38b), считая Землю за сферу.

Здесь: А а¹ = d,

b¹ a¹ = d Cos = d

A b¹ = dS

Если принять этот треугольник за плоский, то можно записать дифференциальные уравнения:

d = dS CosK и d Cos = dSSinK

В результате интегрирования при K = Const получим:

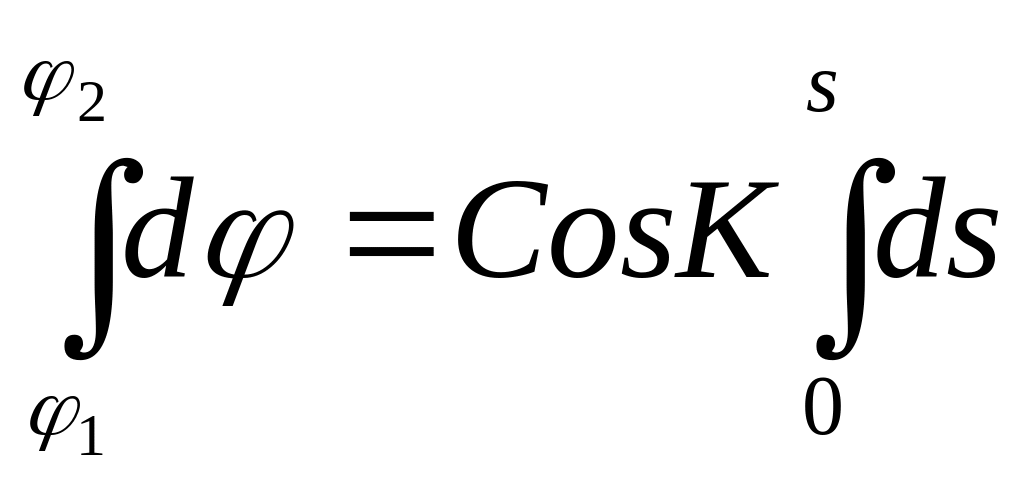₂ - ₁ = S CosK или

РШ = S CosK (1.55)

Для интегрирования dCos значение Cos относят к параллели промежуточной широты, и выносят за знак интеграла:

Cos_n

(₂ - ₁)Cos_n = S SinK или

ОТШ = S SinK (1.56)

Геометрический смысл состоит в том, что ОТШ представляет собой длину отрезка параллели некоторой промежуточной широты _n, заключенной между меридианами

(₁ ₂), а единица измерения морская миля, но не экваториальная минута.

Для вычисления РД воспользуемся соотношением, выражающим длину дуги экватора и параллели.

.

Умножим числитель и знаменатель этого выражения на d.

Теперь, исходя из свойства навигационной карты, можно записать:

, откуда

РД = РМЧ tgK, (1.57)

в тоже время

После искусственных преобразований получим:

или

Для практических задач при небольшом (коротком) пройденном пути можно принять, что Cos изменяется линейно и (в высоких широтах при   10,0 погрешность вычисления долготы будет ощутимой до 2% от ) промежуточная широта приравнивается к средней ,

отсюда окончательно получаем выражение для расчетов разности долгот:

(1.58)

Замена _n на _m дает погрешность в расчетах РД () исходя из формулы: =ОТШtg_mSec_nSin(_n-_m).

По приведенным формулам для нахождения РШ, ОТШ и РД составлены таблицы № 24, 25 в Мореходных таблицах МТ=75. Таблица 25б используется при решении задачи с учетом сфероидичности Земли. В рассчитанные РШ и РД вводят поправки f и g.

Непосредственно по формулам аналитического счисления находят поправки к начальным счислимым координатам _К = _Н +  и _К = _Н + . Вычисление поправок трудоемко, и для расчетов используют ЭВМ.

Аналитический способ расчетов координат намного точнее графического, так как позволяет применять точные формулы сферической тригонометрии и учитывать сфероидичность Земли. Этот способ используется при определении места судна по гиперболическим РНС и спутниковым СРНС.

Аналитическое счисление принято подразделять на три вида: простое, составное и сложное.

Простое аналитическое счисление

Выполняется, когда судно следует одним курсом и нужно найти координаты конечной точки или по координатам начальной и конечной точек рассчитать Курс (К) и плавание на этом курсе (S). По начальным координатам (₁ ₁ ), курсу (К) и плаванию (S) находят РШ, ОТШ и затем РД и получают значения координат конечной точки ₂ = ₁ +РШ ₂ = ₁ + РД.

Решение задачи по вычислению курса (К) и плавания (пройденного расстояния) (S) по известным координатам точек отшествия и пришествия можно выполнить по формулам:

tgK = S = РШ CosecK

Составное аналитическое счисление.

При составном счислении (Рис.1.39) вычислят координаты точки пришествия, если судно плавало несколькими курсами.

Для нахождения координат точки пришествия (Е) рассчитывают РШ и ОТШ для каждого курса, а затем вычисляют (РШ и ОТШ в этом случае называются генеральными ГенРШ и ГенОТШ):

ГенРШ = РШ_N(S) + РШ_S(N)

ГенОТШ = ОТШ_E(W) + ОТШ_W(E).

Nи

С

В ОТШ РШ

ОТШ

РШ D

РШ

А

Рис.1.39 Е

Имея суммы РШ и ОТШ, находим широту точки пришествия (₂) среднюю широту (_М):

₂ = ₁ + ГенРШ, _М = .или +

После чего вычисляем долготу точки пришествия:

РД = , ₂ = ₁ + РД

При обратной задаче, известны:

- разность широт РШ

- отшествие ОТШ

Вычисляют генеральный курс (K) (между точками АЕ) и плавание (S) отрезок АЕ.

tgK_Г = , tgK_Г = , S = ГенРШ CosecK_Г

В составном счислении можно учитывать течение и циркуляцию.

При учете течения принимают курс как направление действия течения (К_Т), а плавание - как произведение времени на скорость течения. Время воздействия течения на судно рассчитывается, исходя из конкретных условий плавания.

(S_Т = Т*V_Т).

При аналитическом счислении циркуляция учитывается по ИКср и плаванию по нему d.

Сложное счисление.

В этом методе аналитического счисления, кроме расчетов РШ и ОТШ на каждом курсе, вычисляются и координаты конечных точек.

Когда аналитическое счисление производится на вычислительных устройствах, сопряженных с указателями курса и скорости, счислимые координаты рассчитываются непрерывно.

В вычислители вводятся математические выражения, позволяющие учитывать сфероидичность Земли.

_i+1 = _I + ; _i+1 = _I +

Здесь М и N – главные радиусы кривизны меридианного эллипса, а V_N и V_E – составляющие скоростей по меридиану и параллели соответственно.

Аналитический расчет элементов сноса течением

При графической прокладке учет сноса течением ведется только графическим способом, решая прямую и обратную задачу.

Эту же графическую работу по учету течения можно выполнить аналитически. При этом рассчитывается угол сноса течением  (Рис. 1.40),

и тогда ПУ = ИК +., или ПУ = ПУ_ - .

Для решения задачи необходимо рассчитать углы и отношение скоростей для ввода в формулы. При прямой задаче используется формула:

Ctg = + Ctgq, (1.59)

где q = К_Т – ИК. Полученный аргумент называется углом течения. Если учитывается дрейф, то q = К_Т - ПУ_,

m = - отношение скорости течения V_T к относительной скорости судна V₀ (относительно воды). В МТ-2000 помещена таблица 2.18а. Для входа в таблицу служат курсовой угол течения q от 0 до 360 и коэффициент m от 0 до 1,0. Знаки у  (+) при сносе вправо и (-) при сносе влево.

При обратной задаче используется формула:

Cosec = , (1.60)

где p = (K_T – ПУ) – угол между направлением течения

Рис. 1.40

и заданной линией пути (направление течения относительно линии пути). Получив угол сноса течением , рассчитывают:

ИК = ПУ -  или ПУ_ = ПУ - .

В МТ-200 приведена таблица 2.18б, в которой по аргументам p при значениях от 0 до 180 ( без учета знака) и m, находят угол сноса течением .

Для расчетов путевой скорости (скорости относительно грунта) в МТ-2000 приведена таблица 2.18в, для входа в которую, является аргумент, рассчитываемый по формуле:

q = p +  и отношение скоростей m = . Полученный из таблицы коэффициент k, используют для расчетов относительной или путевой скоростей.

V = k V₀ или V₀ = (1.61)

Пример 1. Из точки с координатами ₁ = 1127 S, ₁ = 17634 E, следуя ИК = 56, судно совершило плавание S = 810 миль. Определить счислимые координаты в конце плавания.

Решение: РШ = 810*Cos 56 = 810*0,5592 = 452,9 = 732,9 N

ОТШ = 810*Sin 56 = 810*0,829 = 671,5.

_ср = 1127 S + 732,9/2 = 740,6

РД = 671,5/Cos 740,6 = 671,5/0,9883 = 679,4 = 1119,4 E

₂ = 1127 S + 732,9 = 354,1 N

₂ = 17634 E + 1119,4 E = 18748,4 E = (360 - 18748,4 ) = 17211,6 W

Пример 2. Из точки с координатами ₁ = 6228 N, ₁ = 17530 E судно перешло в точку с координатами ₂ = 6939,6 N, ₂ = 16723,5W. Определить ИК и плавание S между названными точками.

Решение. РШ = 6939,6 - 6228 = 711,6. РД = - 16723,5 - 17530 = - 34253,5= 1706,5 Е.

_СР = 6228 + 335,8 = 6603,8 N. ОТШ = +1026,5 Сos 6603,8 = 416,8

tg K = 416,8/431,6 = 0,9634, ИК = 44,0. S = 431,6 * Sec 44,0 = 431,6 * 1,3902 = 600

ИК = 44,0; S = 600 миль.

Пример 3. Из точки с координатами ₁ = 3000 N, ₁ = 17000E судно следовало ГКК = 143,. _ГКК = + 2,0, учитывали дрейф 3,0 пр/б и течение NE – 2 узла. Заданным ГГК судно прошло 3 часа с скоростью 16 узлов. Определить координаты точки пришествия.

Решение. Решим задачу в табличной форме. Расчет будем вести по двум курсам и плаванию по ним. ПУ_ = 142,0, S = 48 миль и К_Т = 45,0 S_T = 6,0 миль

ГКК	ГКК	ИК		ПУ	S	РШ	ОТШ
143,0	+2,0	145,0	- 3,0	142,0	48,0	-37,82	+29,55
Течение		45	-	45	6,0	+4,24	+4,24
					Ген РШ	-33,58 ОТШ	+33,79

_СР = 3000 N - 33,58/2 = 2943,2N. РД = 33,79/Cos 2943,2 = 33,79/0,8685 = 38,9

₂ = 3000 N – 033,6 = 29 26,4N; ₂ = 17000E + 033,8 = 17033,8 E

Пример №4. Следуя ИК = 256,0 и скоростью V = 14 узлов, начали учитывать течение

К_Т = 190,0 и V_T = 2,0 узла. Рассчитать аналитически угол сноса течением .

Решение: Вначале определяем q = 190 – 256 = - 66 и m = = 0,1428

Находим угол сноса течением: Ctg  = + Ctg66 = - 7,6653 + 0,4452 = - 7,2201

 = - 8,0 ПУ = 256 – 8 = 248,0

Пример №5. Судно следует по путевому углу ПУ = 123,, имея относительную скорость

V₀ = 14 узлов, начали учитывать течение К_Т = 45,0 и V_T = 2,0 узла. Определить аналитически ПУ.

Решение: p = 45 – 123 = -78,0. Аргумент m = 0,1428 из предыдущей задачи

Cosec  = = - 7,159.

 = - 8,0. ПУ = 123 – (-)8,0 = 131,0

Контрольные вопросы

1. В каких случаях применяется аналитическое (письменное) счисление?

2. Как учитывают дрейф и течение при аналитическом счислении?

3. Какие виды аналитического (письменного) счисления Вы знаете?

4. Что такое генеральный курс?

5. В каких единицах измеряется отшествие?