10.2. Методический инструментарий прогнозного анализа экономических показателей

Успешность бизнеса в любой сфере деятельности основыва­ется на эффективном планировании, которое, в свою очередь, базируется на точности прогнозного анализа. Прогнозный ана­лиз ориентирован на изучение возможных сценариев развития предприятия в определенных условиях и допущениях. Видение перспективы позволяет своевременно обнаруживать риски и уг­розы и принимать соответствующие меры для их предупрежде­ния. Выявление основных тенденций и перспектив развития, создание образа будущего предприятия, определение потенци­альных возможностей и угроз — основа научного обоснования планов и выработки стратегической и тактической политики предприятия, направленных на достижение его конечных целей.

В настоящее время насчитывается более 100 различных методов и процедур экономического прогнозирования, которые можно условно объединить в несколько групп:

а) эвристические (интуитивные) методы, базирующиеся на экспертных оценках изучаемого объекта;

б) методы, основанные на экстраполяции выявленных тен­денций;

в) эконометрические методы, основанные на исследовании и моделировании причинно-следственных связей между экономи­ческими явлениями.

Эвристические методы относятся к неформальным методам решения экономических задач. Они используются в основном для прогнозирования состояния объекта в условиях частичной или полной неопределенности, когда основным источником по­лучения необходимых сведений служит интеллектуальный по­тенциал профессионалов, работающих в определенных сферах науки и бизнеса.

Наиболее распространенным из них является метод эксперт­ных оценок — организованный сбор суждений и предложений специалистов (экспертов) по исследуемой проблеме с последу­ющей обработкой полученных ответов.

Основой данного метода является опрос специалистов, кото­рый может быть индивидуальным, коллективным, очным, заоч­ным, анонимным и так далее. Организаторы опроса определяют объект и цели экспертизы, подбирают экспертов, проверяют их компе­тентность, анализируют и обобщают результаты экспертизы.

Основные разновидности метода экспертных оценок:

а) метод «мозговой атаки» или конференции идей — поиск новых идей, их широкое обсуждение и конструктивная крити­ка, где генерирование идей происходит в процессе творческого спора и личного контакта специалистов. При этом необходимо четко сформулировать проблему, выделив в ней центральное звено; поддерживать идею любого рода, даже если она кажется сомнительной; не прекращать обсуждение и поощрять любую идею, чтобы участники не чувствовали скованности;

б) метод «мозгового штурма»: одна группа экспертов выдви­гает идеи, а другая их анализирует;

в) синектический метод предполагает использование при ге­нерировании идей аналогий из других областей знаний или фантастики;

г) метод Дельфи — анонимный опрос специалистов по заранее подготовленным вопросам с последующей статистической обработкой информации. После обобщения результатов повторно запрашивается мнение специалистов по спорным вопросам. В итоге обеспечивается переход от интуитивных форм мышления к дискуссионным формам. Для этого метода характерны, изолированность в работе и независимость суждений каждого члена экспертной группы;

д) метод «дерева целей» — использование иерархической структуры решения проблемы путем разделения общей цели на I подцели. Вершина дерева целей представляет собой цели, а «ветви» — это связи между ними. Экспертам предлагается оце­нить структуру модели системы в целом и дать предложения по ее совершенствованию. Результаты анонимного анкетирования обобщаются и доводятся до экспертов, что позволяет им кор­ректировать свои суждения на основе полученной информации;

е) метод ПАТТЕРН — помощь планированию посредством количественной оценки технических данных. Изучаемая про­блема расчленяется на ряд подпроблем, задач и элементов, ко­торые выстраиваются в «дерево решений». Оценки отдельных экспертов подвергаются открытому обсуждению, в результате чего извлекается польза от делового общения экспертов, хотя не исключаются отрицательные последствия конформизма (давле­ние авторитетов);

ж) метод сценариев — экспертная оценка возможных вариан­тов развития событий и выбор наиболее реальных и благоприят­ных. Один из эффективных средств прогнозирования. Сцена­рий — это модель будущего состояния предприятия, которая описывает возможный ход событий, рассматривает факторы, которые могут оказать влияние на ход предполагаемых событий. Обычно в качестве базового сценария рассматривается наиболее вероятный вариант, который служит базой для принятия реше­ния. Другие варианты (оптимистический, пессимистический) считаются альтернативными.

Использование сценарного прогнозирования обеспечивает более глубокое понимание сложившейся ситуации и ее развития в будущем, оценку потенциальных рисков, выявление благопри­ятных возможностей для достижения целей предприятия.

Методы экстраполяции основываются на экономико-статис­тических методах обработки данных за прошлые периоды, опре­деления тенденций развития изучаемого явления в предпрогнозном периоде и проекции найденной закономерности на буду­щее. Экстраполирование установленной закономерности за пределы динамического ряда основано на предположении, что начавшееся изменение переменной будет продолжаться такими же темпами и в будущем. Необходимыми предпосылками полу­чения надежных результатов экстраполяции являются стабиль­ность экономических условий, достаточное количество и досто­верность информации о прошлом.

Наиболее простым методом прогнозирования является при­менение среднего абсолютного прироста и среднего темпа роста динамического ряда. Прогнозируемое значение переменной для любой даты прогнозного периода можно определить по форму­лам:

или

где — начальный уровень ряда;

— средний абсолютный прирост изучаемого показателя, рассчитанный по средней арифметической;

— порядковый номер даты (года, квартала, месяца);

— средний темп роста исследуемого показателя, опреде­ляемый по средней геометрической:

где Y_t — уровень последнего периода;

У₁ — уровень первого периода;

t — число уровней.

На основании полученных данных (табл. 10.1) рассчитаем про­гнозную величину капитала на следующий, одиннадцатый год:

• на базе среднего абсолютного прироста:

• на базе среднего темпа роста:

Таблица 10.1 Исходная информация для расчета среднего абсолютного прироста и темпа роста собственного капитала предприятия

Номер года	1	2	3	4	5	6	7	8	9	10	Сред ний
Капитал, млн руб.	50	52	54,6	55,7	57,4	58	60,3	61,5	63	65,3
Абсолютный прирост капи­тала		+2	+2,6	+1,1	+1,7	+0,6	+2,3	+1,2	+1,5	+2,3	+1,7
Индекс роста (цепной)	—	1,04	1,05	1,02	1,03	1,01	1,04	1,02	1,025	1,036	1,03

Аналогично определяется прогнозный уровень исследуемого показателя и на более отдаленную перспективу.

Рассмотренные методы анализа динамических рядов, позво­ляющие выявить скорость и интенсивность развития исследу­емого явления, — довольно распространенные и легко осуще­ствимые способы прогнозирования, поскольку просты в приме­нении и требуют минимума информации для расчета.

Более точный прогноз развития экономических явлений по­лучают на основе трендовых моделей, которые отражают основ­ную тенденцию динамического ряда, свободную от краткосрочной флуктуации, вызванной разными случайными факторами. Основная тенденция развития обычно выявляется следующими механическими методами: укрупнение интервалов, скользящая средняя и аналитическое выравнивание. Скользящие средние позволяют сгладить как случайные, так и сезонные колебания и выявить основную тенденцию временного ряда.

Наиболее эффективным способом выявления тренда, выража­ющего основную тенденцию временного ряда, является аналити-­

ческое выравнивание динамического ряда с помощью регрессионно­го анализа, которое может производиться по прямой, параболе, гиперболе, экспоненте. Суть его состоит в подборе линии регрес­сии по данным наблюдений таким образом, чтобы квадраты их отклонений от линии регрессии были минимальными:

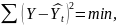
где Y— фактические уровни временного ряда;

Y_t — выравненные уровни временного ряда.

Рассмотрим технику аналитического выравнивания приве­денного динамического ряда по прямой

где а и b — параметры оценки;

t — номер периода.

Параметры прямой, удовлетворяющие методу наименьших квадратов, находятся с помощью следующей системы уравнений:

где у — фактические уровни;

n — число членов ряда динамики.

Подставим полученные суммы (табл. 11.2) в вышеприведен­ную систему уравнений:

Умножая первое уравнение на 5,5, а затем вычитая его из второго уравнения, находим значение Ь:

82,5b=131,8;

b=1,6.

Расчет сумм методом наименьших квадратов

t	У	ty	t2	Yt
1	50,0	50,0	1	50,6
2	52,0	104,0	4	52,2
3	54,6	163,8	9	53,8
4	55,7	222,8	16	55,4
5	57,4	287,0	25	57,0
6	58,0	348,0	36	58,6
7	60,3	422,1	49	60,2
8	61,5	492,0	64	61,8
9	63,0	567,0	81	63,4
10	65,3	653,0	100	65,0
£55	£577,8	£3309,7	£385	£578

Подставляя b в первое уравнение, находим значение а:

Уравнение прямой будет иметь вид

Y_t = 49 + 1,6/.

Прогноз на 11-й год составит

Y_t = 49 + 1,6 * 11 = 66,6 млн руб.

Данный пример показывает, что метод наименьших квадра­тов — довольно удобный способ расчета линии тренда. Резуль­таты прогнозов обычно достаточно точны для краткосрочного прогнозирования. Расчет доверительного интервала предсказан­ных значений существенно повышает качество прогноза.

Вместе с тем механические методы обработки временных ря­дов имеют достаточно много ограничений:

1) не могут быть использованы, если не накоплена ретроспек­тивная информация в необходимом объеме об изучаемом яв­лении (например, для нового изделия, нового вида оборудо­вания);

2) прогнозы, основанные на экстраполировании тренда, пред­полагают продолжение, а не изменение тенденции развития, т.е. не учитывают поворотные точки, которые очень важны в практическом менеджменте;

3) прогнозирование развития на основании изучения одного динамического ряда имеет ограниченное применение и в силу того, что здесь не учитывается взаимосвязь изучаемого явления с другими. Комплексный подход предполагает ис­следование причинно-следственной связи между многими переменными и измерение ее тесноты, что достигается с по­мощью эконометрики. С помощью математических моделей, количественно отража­ющих связь между многими переменными, эконометрика объяс­няет причины изменения экономических явлений в прошлом и дает прогнозы поведения их в будущем.

В АХД наиболее широкое применение получили регрессион­ные и дискриминантные модели.

Пример расчета, оценки и практического использования ре­грессионной модели для прогнозирования уровня результатив­ного показателя показаны в главе 6. Напомним, что коэффи­циенты уравнения множественной регрессии (b₁, Ь₂,…, b_п) при соответствующих факторных признаках {х₁, х₂,…-, х_п) показы­вают, на сколько единиц изменяется величина результативно­го признака с изменением факторного на единицу его измере­ния:

Если в полученное уравнение связи подставить прогнозный уровень факторных показателей, то можно получить прогнози­руемое значение моделируемого показателя.

Дискриминантные модели получили широкое применение для оценки и прогнозирования кредитоспособности и риска банк­ротства предприятия — это известные модели Альтмана, Лиса, Таффлера, Тишоу и других западных экономистов.

Для их разработки требуется достаточно большая выборка данных, желательно по предприятиям одной отрасли, посколь­ку многие показатели могут быть несопоставимы из-за разной структуры капитала и скорости его оборачиваемости в различ­ных отраслях экономики. Затем все множество объектов разби­вается, как правило, на три группы: к первой группе относятся финансово устойчивые предприятия, ко второй — проблемные или обанкротившиеся предприятия, к третьей— остальные. В качестве обучающих выборок используют первую и вторую группы предприятий. Признаки, которые используются для рас­познавания подмножеств, называются дискриминантными пе­ременными. Количество дискриминантных переменных не ог­раничено, но их число должно быть меньше числа объектов на­блюдения. В процессе дискриминантного анализа производится пошаговый отбор переменных, обеспечивающий наилучшее разичие групп. После этого рассчитываются коэффициенты диск­риминацией функции и константы дискриминации.

Основываясь на данной методике и используя компьютерную программу, нами разработана дискриминантная функция для диагностики риска банкротства сельскохозяйственных предпри­ятий:

Z = 0,111 x₁ + 13,239 х₂ + 1,676 x₃ + 0,515х₄ + 3,80х₅,

где х₁ — доля собственного оборотного капитала в формировании оборотных активов, коэффициент;

х₂ — приходится оборотного капитала на рубль основного, руб.;

х₃ — коэффициент оборачиваемости совокупного капитала;

х₄ — рентабельность активов предприятия, %;

х₅ — коэффициент финансовой независимости (доля собствен­ного капитала в общей валюте баланса).

Константа дискриминации для приведенной модели — 8.

Подставляя в данное уравнение фактический или прогноз­ный уровень факторных показателей, можно довольно быстро провести экспресс-анализ финансового состояния сельскохозяй­ственных предприятий и достаточно точно оценить степень ве­роятности их банкротства.

Если величина Z-счета для тестируемого предприятия боль­ше 8, то риск банкротства отсутствует. При значении Z-счета меньше 8 риск банкротства присутствует: от 8 до 5 — неболь­шой, от 5 до 3 — средний, ниже 3 — большой, ниже 1 — 100%-ная несостоятельность.