6.2. Использование способа парной корреляции для изучения стохастических зависимостей
В анализе используются парная и множественная корреляции.
Парная корреляция – это корреляционная зависимость между двумя признаками.
Простейшим уравнением, которое характеризует прямолинейную зависимость между двумя признаками, является уравнение прямой линии
где
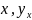– соответственно
независимый и зависимый признаки
уравнения;
– параметры
уравнения регрессии.
Количество наблюдений при прямолинейной зависимости должно быть не менее шести (годы, предприятия или цехи).
В качестве примера прямолинейной зависимости используются данные об изменении фондовооруженности и производительности труда работающих, приведенные в табл. 8.1.
Таблица 8.1 Исходные данные и вспомогательные расчеты для определения зависимости между фондовооруженностью и производительностью труда работающих
Годы, месяцы |
Производительность труда работающих у, тыс. р. |
Фондовооруженность работающих х, тыс. р. |
ху |
х2 |
у2 |
1 |
6,2 |
1,6 |
9,9 |
2,6 |
38,4 |
2 |
6,6 |
1,8 |
11,9 |
3,2 |
43,6 |
3 |
6,9 |
2,0 |
13,8 |
4,0 |
47,6 |
4 |
6,8 |
2,0 |
13,6 |
4,0 |
46,2 |
5 |
7,3 |
2,3 |
16,8 |
5,3 |
53,3 |
6 |
7,6 |
2,4 |
18,2 |
5,8 |
57,8 |
7 |
8,6 |
2,5 |
21,5 |
6,3 |
74,0 |
8 |
9,1 |
2,6 |
23,7 |
6,8 |
82,8 |
9 |
10,6 |
2,6 |
27,6 |
6,8 |
112,4 |
10 |
11,2 |
2,8 |
31,4 |
7,8 |
125,4 |
Итого |
0 |
0 |
0 |
0 |
0 |
При планировании роста производительности труда важно определить ее повышение в зависимости от увеличения фондовооруженности.
Связь между производительностью и фондовооруженностью труда можно выразить в виде уравнения прямой линии
где
– постоянная
величина, не связанная с изменением
данного фактора.
Для выяснения связи рассчитаем коэффициент корреляции по формуле
Коэффициент корреляции 0,88 выражает связь между фондовооруженностью и производительностью труда и по абсолютной величине может принимать значения в пределах от нуля до единицы. Если никакой связи между двумя изучаемыми показателями нет, то он будет равен нулю. Если же между исследуемыми признаками существует тесная связь, то коэффициент корреляции близок к единице.
Если коэффициент корреляции равен единице, значит, результативный признак полностью зависит от признака-фактора, т.е., по существу, корреляционная зависимость совпадает с функциональной. Следовательно, чем ближе коэффициент корреляции к единице, тем теснее связь между изучаемыми явлениями и наоборот.
Для нахождения неизвестных параметров а в решаем систему так называемых нормальных уравнений:
.
Величина
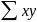определяется умножением значений
и
и последующим суммированием полученного
произведения. Для исчисления величины
следует значения
возвести в квадрат и полученные результаты
суммировать.
Числовые
значения
рассчитываются на основании фактических
исходных данных, представленных в табл.
8.1.
В результате подстановки данных табл. 8.1. в систему уравнений получаем:
Из данной системы уравнений получаем:
Уравнение, отражающее связь между фондовооруженностью и производительностью работающих, имеет следующий вид:
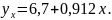
Следовательно, увеличение фондовооруженности труда работающих на 1000 р. приводит к росту производительности труда на 912 р. Эти данные учитываются при перспективном и текущем планировании повышения производительности труда.