Тема 2.2. Исследование функции с помощью производной.

Студент должен:

знать:

• определение точки перегиба;

• определение асимптот графика функций;

• общую схему исследования функции.

уметь:

• применять вторую производную для нахождения точек перегиба функции;

• устанавливать направление выпуклости графика функции;

• находить асимптоты графика функции;

• исследовать функцию по общей схеме и строить ее график.

Признак монотонности, необходимые и достаточные условия экстремумов. Промежутки выпуклости и вогнутости, точки перегиба. Вертикальные и наклонные асимптоты. Общая схема исследования функции одной переменной.

Вопросы для самоконтроля:

1. Каковы признаки возрастания и убывания функции?

2. Приведите пример, показывающий, что обращение производной в нуль не является достаточным условием экстремума функции.

3. Как находятся интервалы выпуклости и вогнутости и точки перегиба?

Раздел 3. Интегральное исчисление

Тема 3.1. Неопределенный интеграл

Студент должен:

знать:

• символику и определение неопределенного интеграла;

• свойства неопределенного интеграла;

• методы интегрирования (непосредственное интегрирование, по частям, введение новой переменной);

уметь:

• вычислять неопределенные интегралы.

Первообразная и неопределенный интеграл. Основные свойства. Таблица основных интегралов.

Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.

Вопросы для самоконтроля:

1. Сформулируйте определение первообразной функции.

2. Каковы основные методы интегрирования функций?

Тема 3.2. Определенный интеграл

Студент должен:

знать:

• символику и определение определенного интеграла;

• свойства определенного интеграла;

• методы вычисления определенного интеграла.

уметь:

• вычислять определенные интегралы;

• решать несложные задачи на применение определенного интеграла.

Определенный интеграл. Определение, геометрический смысл, свойства. Формула Ньютона-Лейбница.

Замена переменной и интегрирование по частям в определенном интеграле. Приближенное вычисление определенных интегралов.

Вычисление геометрических, механических, физических величин с помощью определенного интеграла.

Вопросы для самоконтроля:

1. Что называется определенным интегралом данной функции 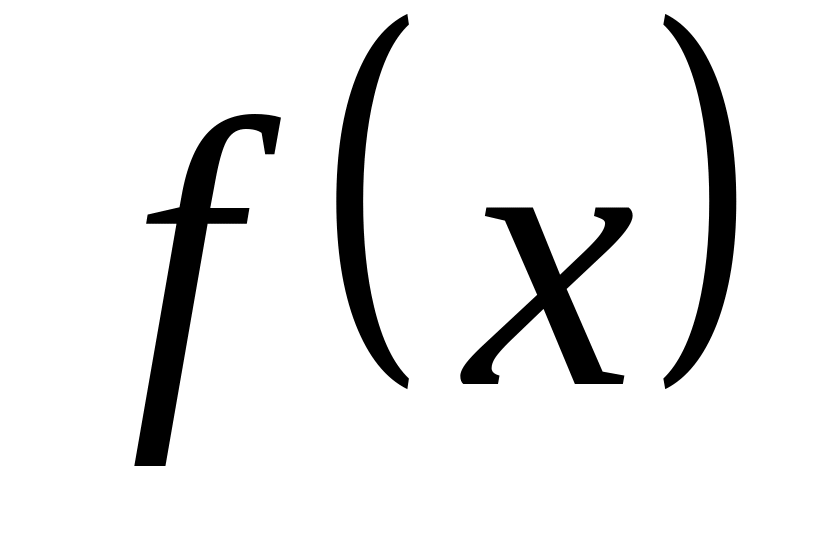на данном отрезке 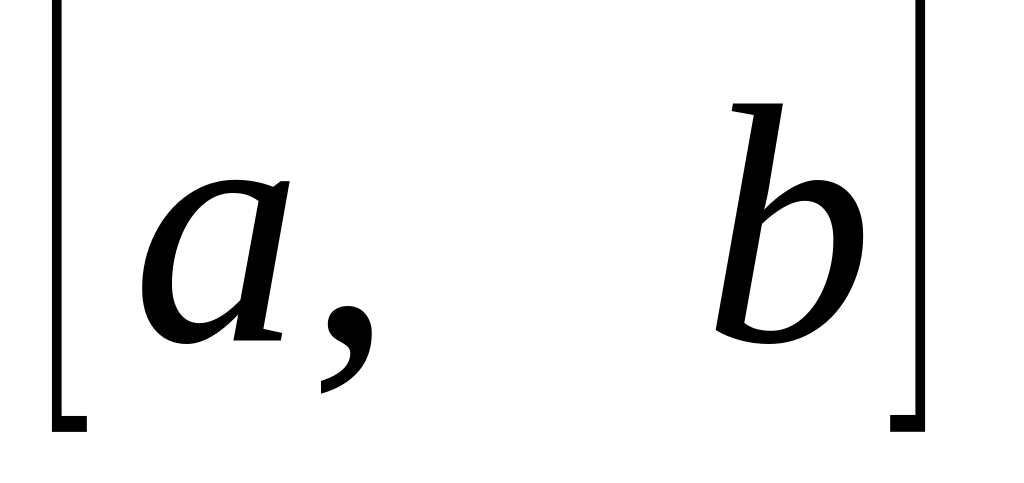? Каковы его основные свойства и геометрический смысл?

2. Напишите формулу Ньютона-Лейбница.

3. В чем состоит способ замены переменной и интегрирования по частям для определенного интеграла?

2. Инструкция по выполнению контрольной работы

1. В процессе изучения предмета студент должен выполнить контрольную работу, главная цель которой – оказать студенту помощь в изучении предмета. Рецензия на эту работу позволяет студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы, на желательное направление дальнейшей работы.

2. Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по материалу, соответствующему этому заданию.

3. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная контрольная работа не дает возможности преподавателю указать студенту на недостатки в его работе, в усвоении им учебного материала, в результате чего студент не приобретает необходимых знаний и может оказаться неподготовленным к зачету.