3.3. Предел числовой последовательности

Определение1. Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число , то говорят, что задана числовая последовательность {a_n}:

Другими словами, числовая последовательность – это функция натурального аргумента:

Числа называются членами последовательности, а число - общим или n-м членом данной последовательности.

Пример 5. Пусть . Вычислить первые пять членов этой последовательности.

Решение. Вычисляем по формуле общего члена последовательности:

и т.д. Эта последовательность имеет вид:

Рассмотрим последовательность

Легко видеть, что , и, следовательно, с возрастанием номера n приближается к 8. Поставим перед собой задачу придать этому утверждению точную математическую формулировку. С этой целью сначала ответим на следующий вопрос: каким должно быть n, чтобы модуль разности был меньше 0,001? Так как

,

то неравенство выполняется для любого n>1000. Для произвольного положительного числа неравенство

равносильно неравенству . В этом случае говорят, что предел последовательности равен 8, и пишут:

Определение 2. Число а называется пределом числовой последовательности {a_n}, если для каждого заданного числа >0 найдется такое натуральное число N, что для всех членов последовательности с номерами n>N выполняется неравенство

.

В этом случае пишут:

и говорят: «Последовательность {a_n} имеет пределом число а» или «Последовательность {a_n} сходится к числу а».

Определение 3. Последовательность, имеющая предел, называется сходящейся, а не имеющая предела – расходящейся.

Выясним геометрический смысл предела числовой последовательности.

Расположим члены последовательности на числовой прямой. Неравенство равносильно двойному неравенству , соответствующему попаданию членов последовательности в -окрестность точки а.

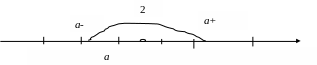
Итак, число а есть предел числовой последовательности {a_n}, если для любого найдется номер N, начиная с которого (при n>N) все члены последовательности будут заключены в -окрестности точки а, какой бы малой она ни была. Вне этой -окрестности может быть лишь конечное число членов данной последовательности.

3.4. Предел функции

С понятием предела числовой последовательности тесно связано понятие предела функции в бесконечности. Если в первом случае переменная n, возрастая, принимает лишь целые значения, то во втором случае переменная х, изменяясь принимает любые значения.

Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а.

Определение 4. Число В называется пределом функции f(x) при х, стремящемся к а (или в точке а), если для любой последовательности допустимых значений аргумента х_n, , , сходящейся к а (т.е. ), последовательность соответствующих значений функции f(x_n), сходится к числу В. В этом случае пишут:

.

Смысл определения предела функции f(x) в точке а состоит в том, что для всех значений х достаточно близких к а, значения функции f(x) как угодно мало отличаются от числа В (по абсолютной величине).

Замечание 1. Определение предела не требует существования функции в самой точке а, т.к. рассматривает значения в некоторой окрестности точки а. Другими словами, рассматривая , мы предполагаем, что х стремится к а, но не достигает значения а. Поэтому наличие или отсутствие предела при определяется поведением функции в окрестности точки а, но не связано со значением функции )или его отсутствием) в самой точке а.

Замечание 2. Если при стремлении х к а переменная х принимает лишь значения, меньшие а, или наоборот, лишь значения, большие а, и при этом функция f(x) стремится к некоторому числу , то говорят об односторонних пределах функции f(x) соответственно слева и справа . Очевидно, что определение этих пределов будет аналогично рассмотренному выше.

Разумеется, если = =В, то =В.