Глава 3. Введение в анализ. Пределы

3.1. Понятие функции. График функции

Применение математики к изучению законов природы и к использованию их в различных областях человеческой де6ятльности заставило ввести в математику понятие пере6менной величины и, в противоположность ей, понятие постоянной величины. Переменной величиной называется всякая величина, принимающая в условиях данного процесса различные числовые значения. Постоянная величина в рассматриваемом процессе принимает одно и то же значение.

Величина у называется функцией переменной величины х, (аргумента), если каждому значению переменной х из указанной области ее изменения Х по некоторому закону соответствует вполне определенное значение у, т.е.

Множество Х называют областью определения (существования), а У – областью изменения функции. Символ f называют характеристикой функции, он может обозначать не только математические операции и последовательность их выполнения, а и правило, сформулированное любым способом (словами, таблицей, графиком и т.д), по которому каждому значению х можно найти соответствующее значение у.

Из сформулированного определения следует, что функция считается заданной, если указаны ее область определения Х и закон соответствия f.

Пример 1. Пусть функция задана на отрезке . Тогда область ее определения есть этот отрезок [0; 1]. Вне его функция не определена.

Если функция задана аналитически (формулой) и область ее определения не указана (не задана), то под областью определения функции понимают множество тех значений аргумента, при которых функция имеет смысл, т.е. принимает вполне определенные вещественные значения.

Пример 2. Найти область определения функции

Решение.

Графиком функции называется множество точек плоскости ХОУ, абсциссами которых являются значения аргумента х, а ординатами – значения .

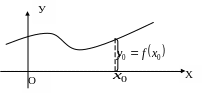
Значение функции , соответствующее значению аргумента х₀, называют ее частным значением.

Пример 3.

Если у есть функция от u, т.е. y=f(u), а и является, в свою очередь, функцией от х: u=(x), то функция называется функцией от функции или сложной функцией от х. При этом: u – промежуточный аргумент; х – независимый аргумент. f(u) называется внешней функцией, и(х) – внутренней. Вид сложной функции определяется внешней функцией (последней операцией над аргументом при вычислении частного значения функции).

Пример 4. Написать формулу, выражающую у как функцию от х, если u=х-6.

Решение.

3.2. Элементарные функции и их графики

Основными элементарными функциями являются следующие:

Степенная функция: где а) n – четное натуральное б) n – нечетное натуральное

число, число.

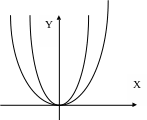
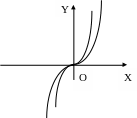
в) n – целое нечетное отрицательное г) n – целое четное.

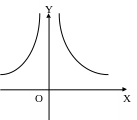число отрицательное число,

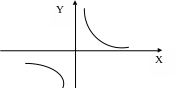
2. Показательная функция - (a>0; a 1).

1. Логарифмическая функция -

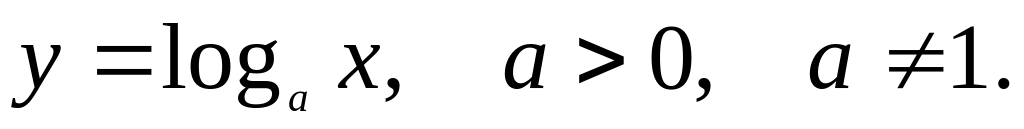
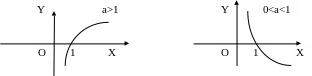
4)Тригонометрические функции

у=sinx, y=cosx, y=tgx, y=ctgx.

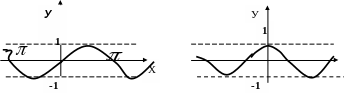
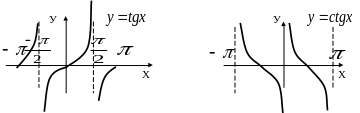
Для наглядности сведем в одну таблицу рассмотренные элементарные функции. При этом заметим, что мы не давали определения таких понятий, как монотонность, ограниченность, четность, нечетность и периодичность, которые определяются и рассматриваются в школьном курсе математики.

Функция	Область определения	Множество значений	Ограниченность	Четность, нечетность			Монотонность	Периодичность
Постоянная функция
у=С,		С	да	четная			нет	да Т-любой
Степенная функция
1. n - нечетно			нет	нечетная			возрастает	нет
2. n - четно			нет	четная			нет	нет
3. n - нечетно			нет	нечетная			убывает	нет
4. n - четно			нет	четная			нет	нет
Показательная функция
			нет	общего вида			нет	нет
Логарифмическая функция
			нет	общего вида			возрастает, a>1, убывает, 0<a<1	нет
Тригонометрические функции
			да		нечетная	нет		да
			да		четная	нет		да
	,		нет		нечетная	возрастает		да
	,		нет		нечетная	убывает		да

Обратные тригонометрические функции
			да	нечетная	возрастает	нет
			да	общего вида	убывает	нет
			да	нечетная	возрастает	нет
			да	общего вида	убывает	нет