2.9. Решение задач
Задача 1.
Построить
на прямой точки А(3), В(-2), С(0), D(
),
Е(-3,5).
Решение.
Задача 2.
Определить
расстояние
между точками A, B,
C, D, E
из задачи 1.
Решение.
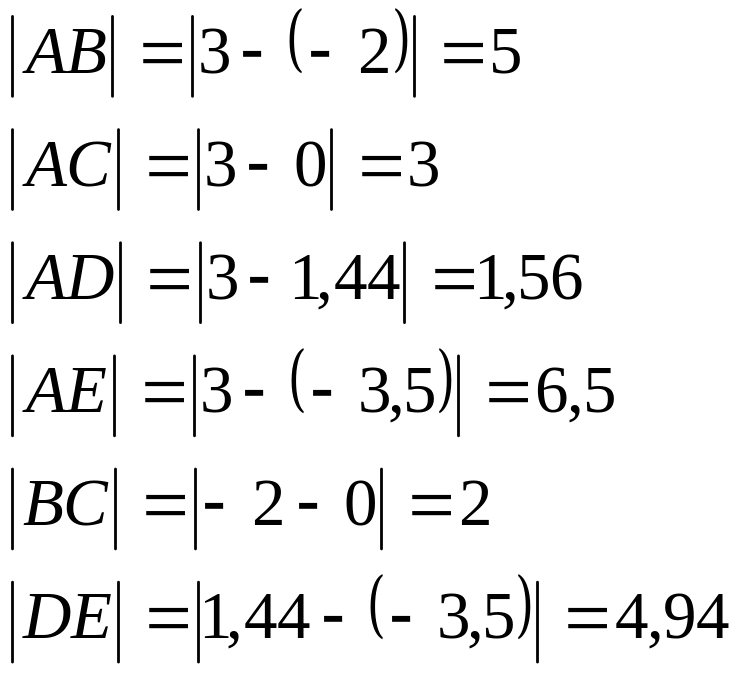
Задача 3.
Отрезок АВ четырьмя точками разделен на 5 равных частей. Определить координату ближайшей к А точке деления, если А(-3), В(7).
Решение.
Пусть
С(х) – искомая точка, тогда
Используя формулу деления отрезка в
данном отношении, находим
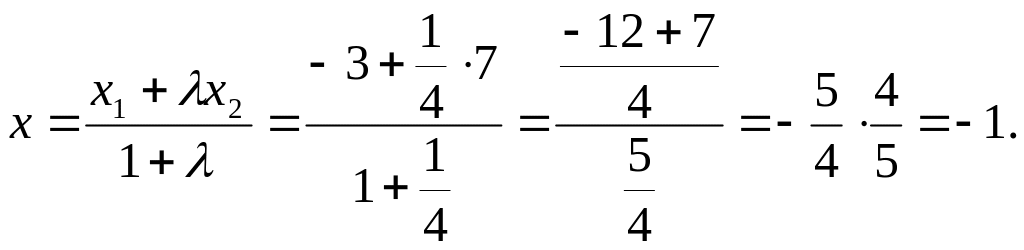
Ответ: С(-1).
Задача 4.
Даны концы отрезка АВ: точки А(1), В(5). Вне отрезка АВ расположена точка С, причем ее расстояние от точки А в три раза больше расстояния от точки В. Определить координату точки С.
Решение.
A
B C(x)
0
1 5 X
Определим
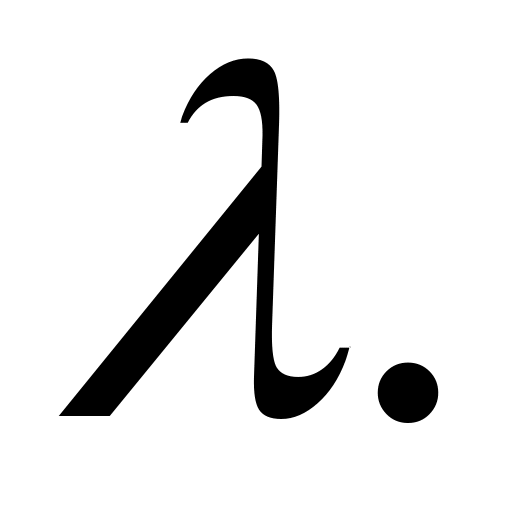
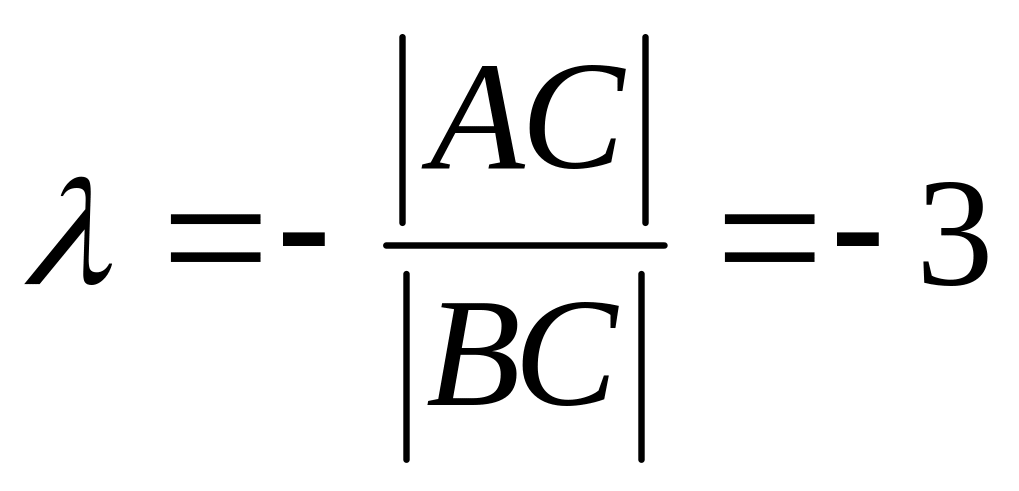
Определим координату (.)С по формуле деления отрезка в данном отношении
Ответ: С(7).
Задача 5.
Даны
точки А(-7), В(-3). Вне отрезка АВ расположены
точки С и D, причем СА=ВD=
.
Определить координаты точек С и D.
Решение.
Найдем координату (.)С аналитически используя формулу деления отрезка в данном отношении. Точка С расположена вне отрезка АВ, т.е.
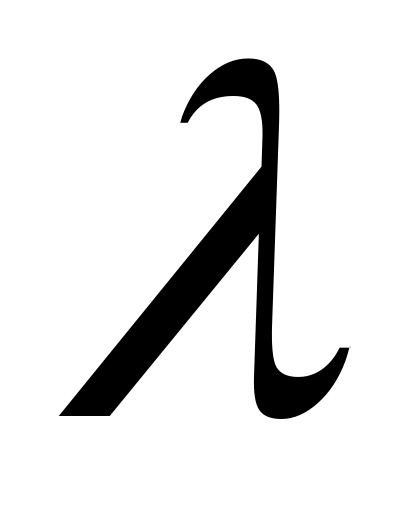- отрицательное число.
Из
условия
т.е.
Откуда
Пусть
или А(-7), В(-3), тогда
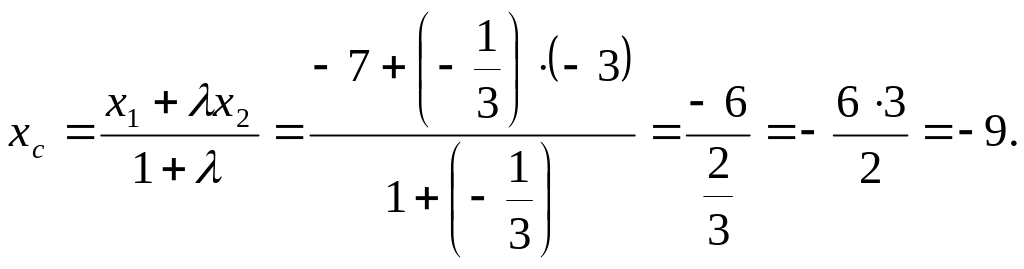
Т.е. С(-9).
Найдем координату точки D. Из условия (.)D лежит вне отрезка
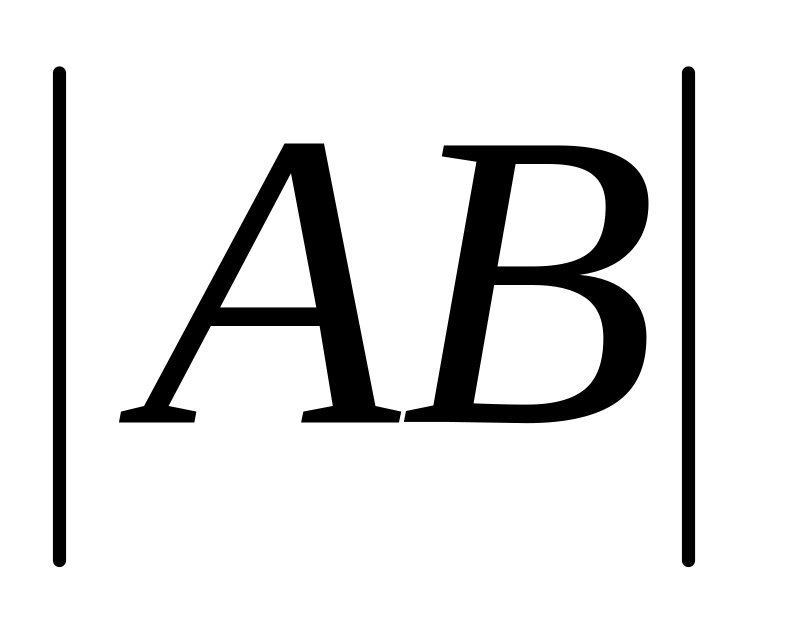и
.
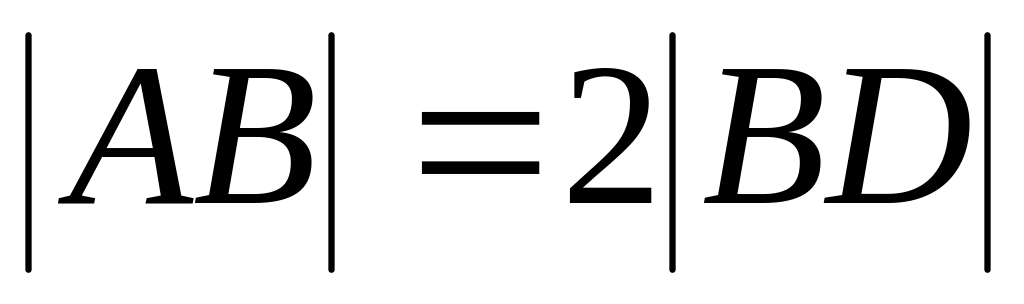Откуда
.
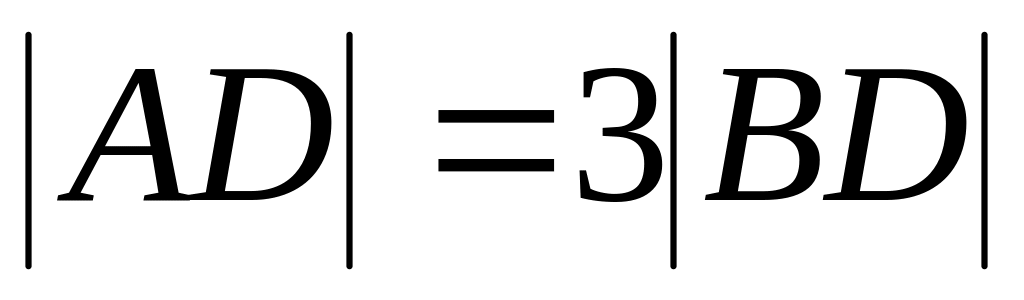Пусть
или В(-3), А(-7). Найдем координату (.)D.
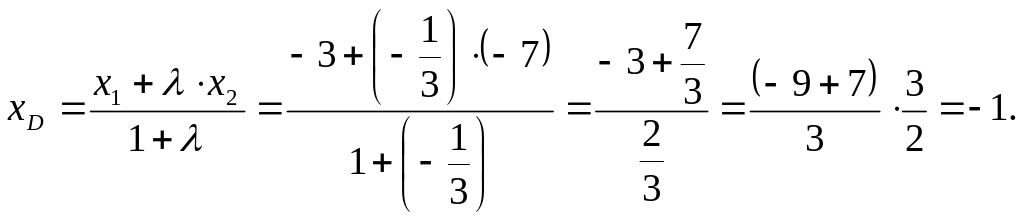
Т.е. D(-1).
Ответ: С(-9); D(-1).
Задача 6.
Построить на координатной плоскости точки А(3;8), В(-5;!4), С(5;-2), D(-4;-3), E(-6;0), F(0;4).
Задача 7.
Определить
расстояние
между точками А(3;8), В(-5;14).
Решение.
Задача 8.
Показать, что треугольник с вершинами А(-3;-3), В(-1;3), С(11;-1) – прямоугольный.
Решение.
Найдем стороны треугольника
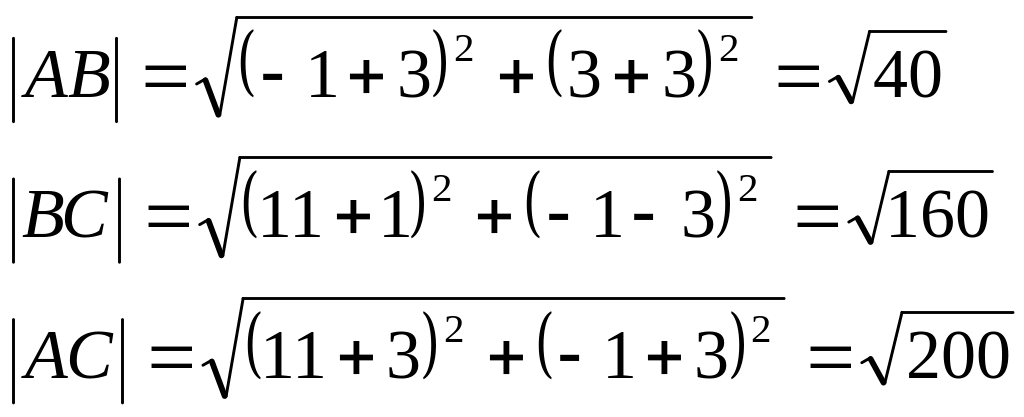
Т.к.
то
Известно, что в прямоугольном треугольнике
сумма квадратов двух сторон равна
квадрату третьей стороны. Отсюда
заключаем, что треугольник АВС –
прямоугольный, а АС – гипотенуза.
Задача 9.
Даны точки А(-2;5), В(4;17) – концы отрезка АВ. На этом отрезке находится точка С, расстояние которой от А в два раза больше расстояния от В. Определить координаты (.)С.
Решение.
Т.к.
,
то
Даны
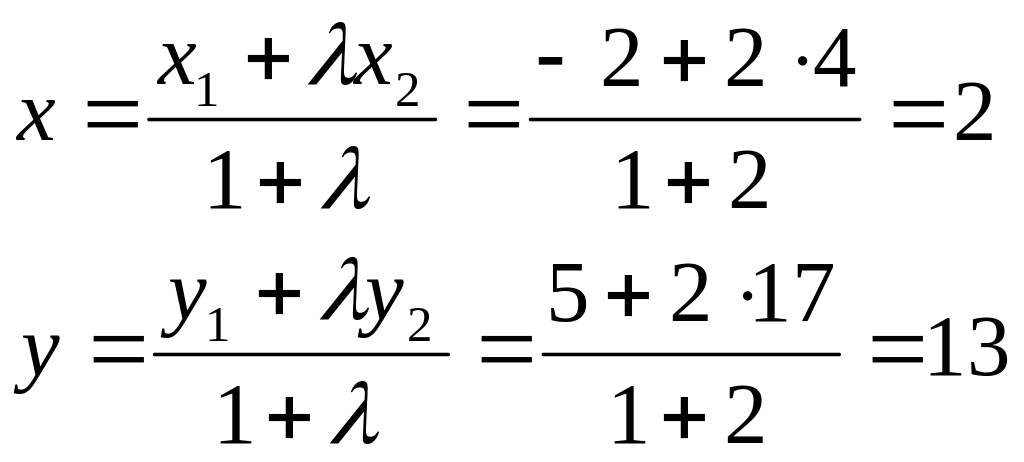
Т.е. С(2;13).
Задача 10.
Показать, что треугольник с вершинами А(2;-1), В(4;2), С(5;1) – равнобедренный.
Задача 11.
Даны вершины треугольника А(-1;-1), В(0;-6), С(-10;-2). Найти длину медианы, проведенной из вершины А. Отв:5.
Задача 12.
Точки А(-5;-3), В(-1;4), С(-1;-7) – три вершины параллелограмма, причем А и С являются противоположными. Найти координаты четвертой вершины.
Решение.
Сделаем схематический чертеж.
A(-5;-3)
B(-1;4)
VvM
Диагонали параллелограмма в точке пересечения М делятся пополам. Значит можно определить координаты точки М по формулам:
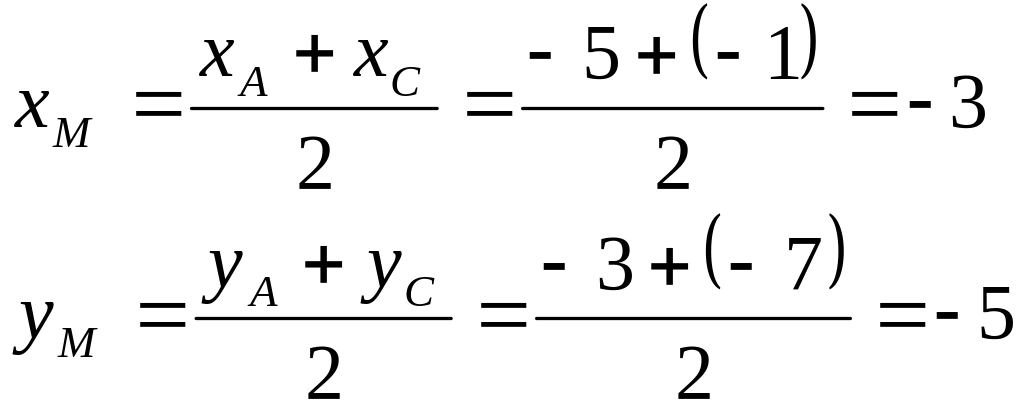
Теперь
можно найти координаты точки D,
применяя те же формулы к отрезку
.
Ответ: D(-5;-14) – искомая вершина.
Задача 13.
Построить прямую 3х-2у-6=0.
Решение.
Прямая 3х-2у-6=0 задана общим уравнением. Для построения прямой найдем точки ее пересечения с осями координат. Сначала ищем точку пересечения с осью Ох. Ордината любой точки, лежащей на оси Ох, равна 0. Поэтому в уравнении прямой положим у=0. Получим 3х-6=0. Отсюда находим х=2.
А(2,0) – точка пересечения прямой с осью Ох.
Аналогично ищем точку пересечения с осью Оу. Если х=0, то –2у-6=0, откуда у=-3, и значит,
В(0,-3) – точка пересечения прямой с осью Оу.
Построив на координатных осях точки А(2,0) и В(0,-3), проведем через них прямую.
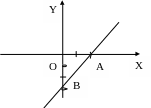
Задача 14.
Построить
прямую
Решение.
П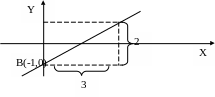
рямая
задана в виде уравнения прямой с угловым
коэффициентом. Здесь b=-1;
k=tg=
На оси ординат откладываем отрезок b=-1
и получаем точку В(0,-1). Через эту точку
проводим прямую, наклоненную к
положительному направлению оси Ох под
углом, тангенс которого равен
Построить прямую 2х-5=0.
Решение.
Запишем уравнение иначе:
Это уравнение прямой, параллельной оси Оу и отсекающей на оси Ох отрезок 2,5.
Примечание: для различных точек у может принимать любое значение, но для каждой из них абсцисса х=2,5.
Задача 16.
Определить параметры k и b для каждой из прямых:
а) 2х-3у=6; б) 2х+3у=0; в) у=-3.
Решение.
а)
Приведем исходное уравнение к виду
уравнения с угловым коэффициентом
y=kx+b:
2х-3у=6;
-3у=-2х+6;
т.е.
;
b=-2.
б)
2х+3у=0;
3у=-2х;
у=
т.е.
;
b=0.
в) у=-3; т.е. у=0х-3; k=0; b=-3.
Задача 17.
Написать уравнение прямой, проходящей через точку А(2,3) и образующей с осью Ох угол 45°.
Решение.
Воспользуемся уравнением y=kx+b.
k=tg45°=1, поэтому уравнение можно записать так: у=х+b. Прямая проходит через точку А(2,3). Это значит, что координаты этой точки удовлетворяют уравнению прямой, т.е. 3=2+b, откуда b=1.
Итак, у=х+1 – искомое уравнение.
Задача 18.
Даны прямые:
Представить их уравнения в общем виде.
Ответ: 2х+5у=0; 2х-3у+9=0.
Задача 19.
Уравнения прямых: а) 3х-2у+4=0; б) 2х-у-1=0 привести к виду уравнения в отрезках.
Решение.
а)
Перенесем свободный член в правую часть
равенства и разделим на него все члены
уравнения:
3х-2у+4=0;
3х-2у=-4;
здесь
б)
2х-у-1=0;
2х-у=1;
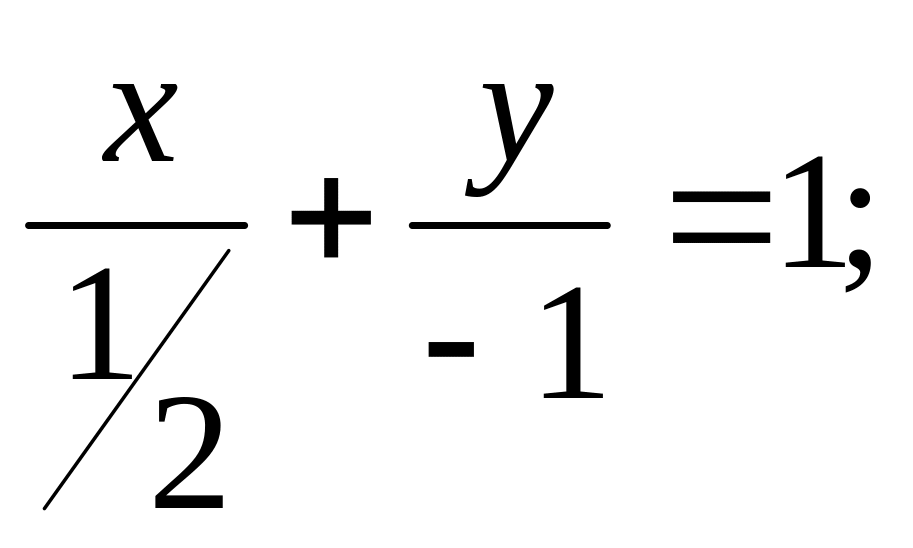здесь
Задача 20.
Уравнения прямых
4х+3у=12;
3х-2у+6=0;
х-2у-1=0
привести к виду уравнений прямых в отрезках. Построить эти прямые.
Ответ:
1)
2)
3)
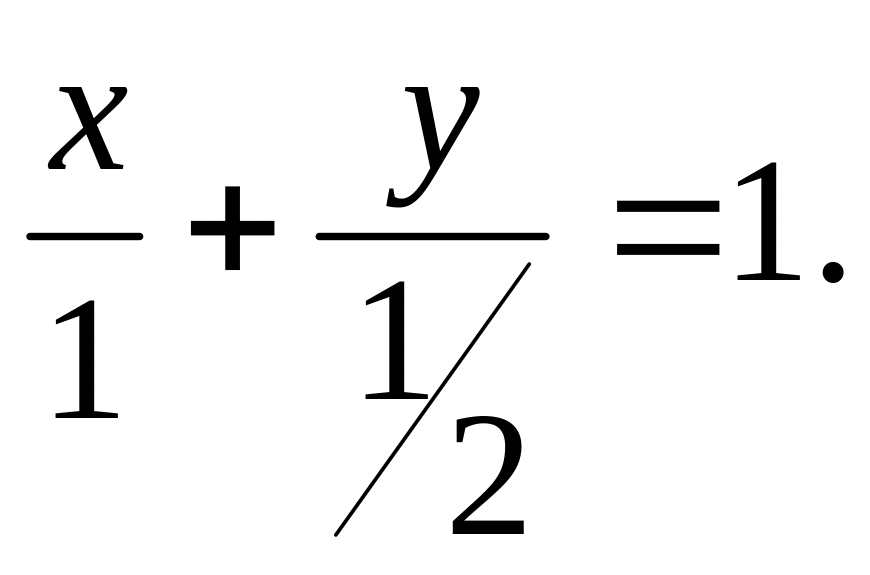
Задача 21.
Определить
длину отрезка прямой
заключенного между точками пересечения
прямой с осями координат.
Ответ: d=10.
Задача 22.
Написать уравнение прямой, проходящей через точки А(3,-1) и В(-5,4). Лежат ли на этой прямой точки D(1,4) и С(-3;2,75)?
Ответ: 5х+8у-7=0; С – лежит; D – не лежит.
Задача 23.
В треугольнике АВС А(-3,0), В(1,6), С(1,0). Написать уравнения его сторон.
Решение.
Построим чертеж.
Уравнение АВ найдем по формуле уравнения прямой, проходящей через две заданные точки.
6(х+3)=4у;
4у-6х-18=0;
2у-3х-9=0;
3х-2у+9=0 – уравнение стороны АВ.
Уравнение стороны ВС: у точек В(1,6) и С(1,0) одинаковая абсцисса. Следовательно х=1 – уравнение стороны ВС.
Точки А и С лежат на оси Ох, следовательно у=0 – уравнение стороны АС.
Задача 24.
В треугольнике АВС А(1,-1), В(3,-5), С(-7,11). Составить уравнение его сторон и уравнение прямой, проходящей через середины сторон АВ и ВС.
Ответ: 3х-у-4=0, 3х+5у-34=0, 3х+2у-1=0, 3х+2у=10.
Задача 25.
Вершины треугольника расположены в точках с координатами А(1,2), В(3,4), С(5,-6). Определить длину высоты, опущенной из вершины А.
Решение.
Составим уравнение стороны треугольника, проходящей через точки А(1,2) и С(5,-6).
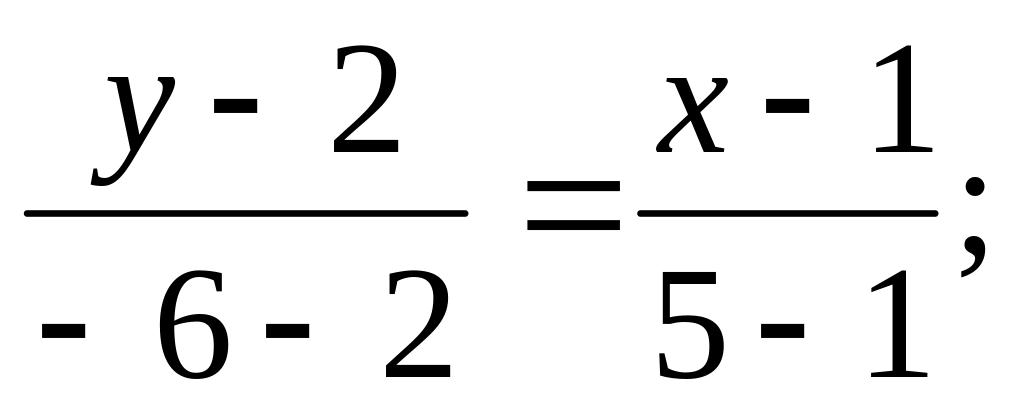2х+у-4=0
– уравнение АС.Определим длину перпендикуляра, опущенного из (.)В на АС.
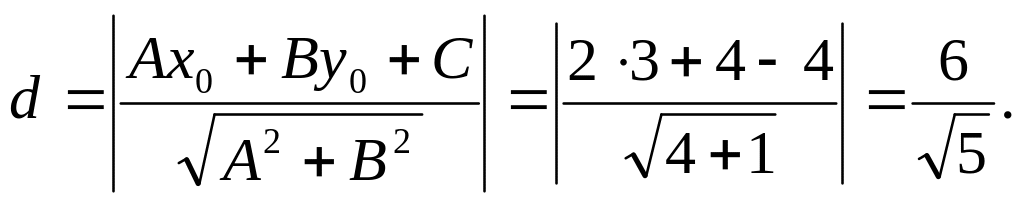
Задача 26.
Найти
точку пересечения
прямых 2х+3у-12=0 и х-у-1=0.
Решение.
Находим решение системы уравнений:
Ответ: М(3,2).
Задача 27.
Даны уравнения сторон треугольника:
х+2у-2=0; 2х+у-13=0; х-2у+6=0.
Показать, что этот треугольник прямоугольный. Найти координаты его вершин.
Решение.
Найдем угловые коэффициенты сторон.
АВ:
х+2у-2=0;
BC:
2x+y-13=0;
AC:
x-2y+6=0;
Условие
перпендикулярности состоит в том, что
угловые коэффициенты сторон
В нашем случае
т.е. стороны АС и ВС перпендикулярны.
Значит треугольник АВС – прямоугольный.
Теперь найдем координаты вершин.
А:
В:
С:
Задача 28.
Дан треугольник АВС с вершинами А(-5,-1), В(-1,4), С(3,2). Через вершину А проведена прямая, параллельная ВС. Через вершину В – прямая, перпендикулярная ВС. Найти точку пересечения проведенных прямых.
Ответ: (-3,8;-1,6).
Задача 29.
Найти
координаты центра и радиус окружности
Ответ:
Задача 30.
Построить
окружность
и прямую 2х-у=0. Найти их точки
пересечения.
Решение.
Для построения окружности найдем ее радиус и координаты центра. Для этого приведем уравнение окружности к виду нормального уравнения, т.е. к виду
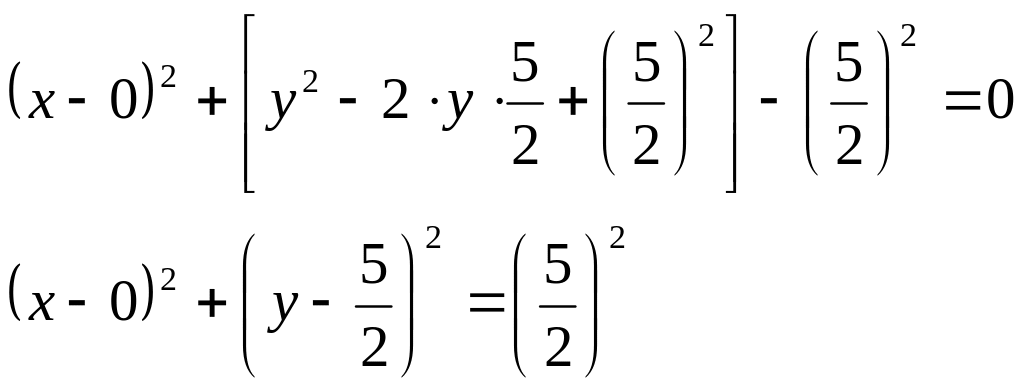
Следовательно
Уравнение линии АВ:
2х-у=0
у=2х
а) х=0; у=0 (.)О;
б) х=2; у=4 (.)В.
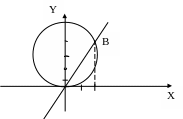
Точки пересечения найдем, решая систему уравнений:
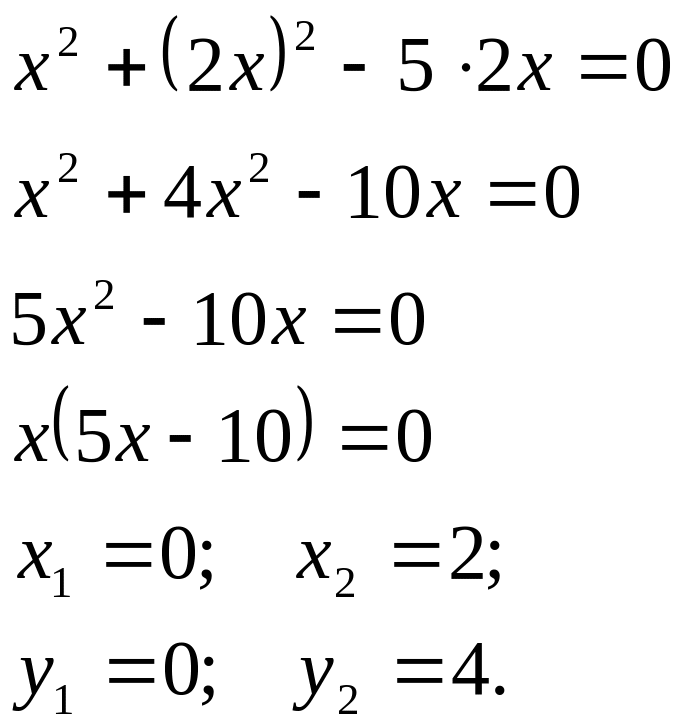
Где О(0;0) и В(2;4) – искомые точки.
Задача 31.
Найти
координаты фокусов и эксцентриситет
эллипса
Решение.
Приведем исходное уравнение к каноническому виду.
Отсюда
Т.к.
а>b, то
Фокусы
и
,
таким образом
Эксцентриситет равен:
Задача 32.
У
гиперболы
найти координаты вершин, фокусов,
эксцентриситет. Сделать чертеж.
Ответ:
Задача 33.
Построить параболы:
Написать координаты их фокусов.
Задача 34.
Написать
уравнение параболы, проходящей через
точки О(0;0) и
и симметричной относительно оси Ох.
Задача 35.
Найти
расстояние между левым фокусом гиперболы
и точкой А, лежащей на асимптоте. Ордината
точки равна 3. Асимптота образует с осью
Ох острый угол.
Решение.
Вычислим координаты фокуса:
a=4;
b=3;
Координаты фокуса: левый фокус F(-5;0).
Асимптота
образует с осью ОХ острый угол.
Следовательно ее уравнение
Точка А имеет ординату 3, найдем абсциссу.
Итак, А(4;3).
Вычислим
расстояние между А(4;3) и
(-5;0):
Задача 36.
Написать
уравнение эллипса, имеющего общие фокусы
с гиперболой
и эксцентриситет
.
Решение.
Найдем фокусы гиперболы:
Найдем полуфокусное расстояние:
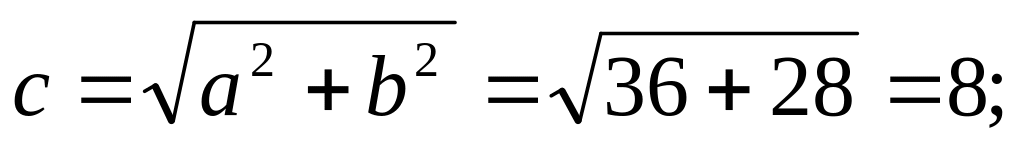
- общие фокусы гиперболы и эллипса.Найдем полуоси эллипса:
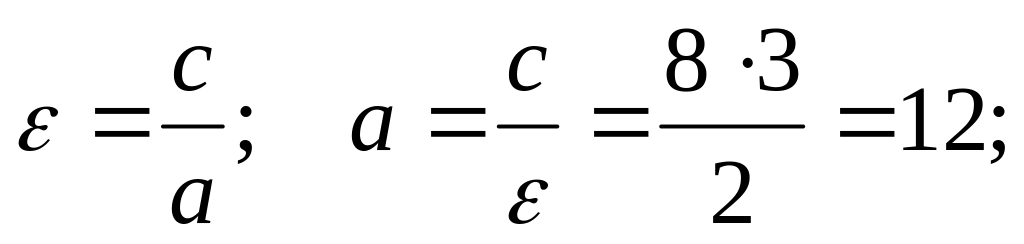
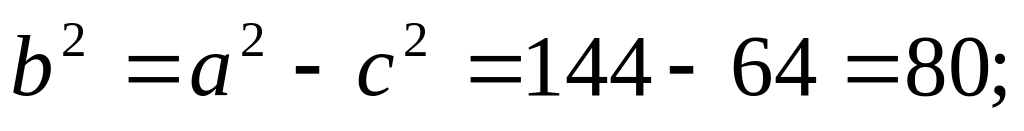
Уравнение эллипса:
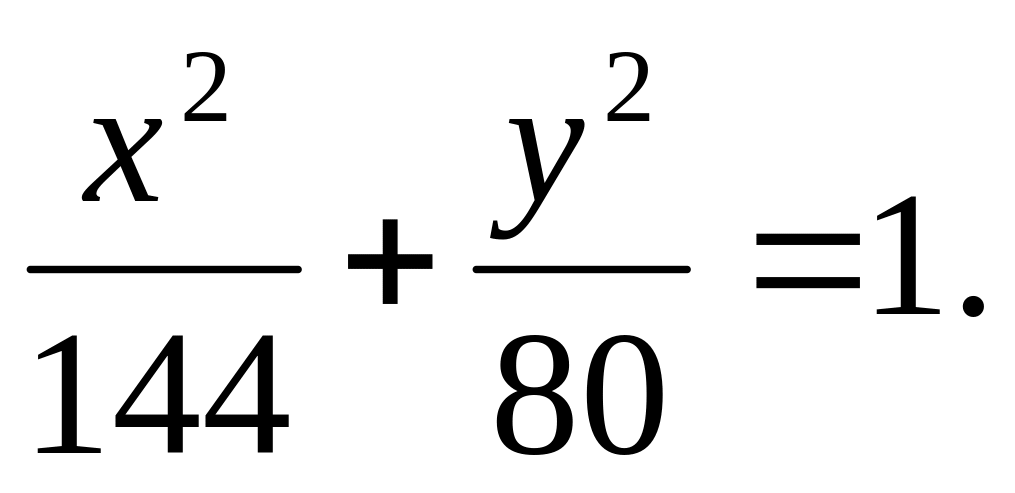
Задача 37.
Найти
точки пересечения эллипса
и прямой х-2у+4=0.
Ответ: (2;3), (-6;-1).
Задача 38.
На
параболе
взята точка А, абсцисса которой равна
–6. Составить уравнение перпендикуляра,
восстановленного к отрезку AF
в его середине. F(0;1) –
координаты фокуса параболы.
Решение.
Найдем координаты (.)А:
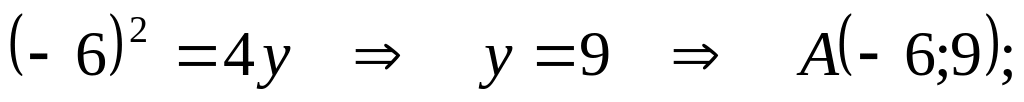
середина отрезка AF точка
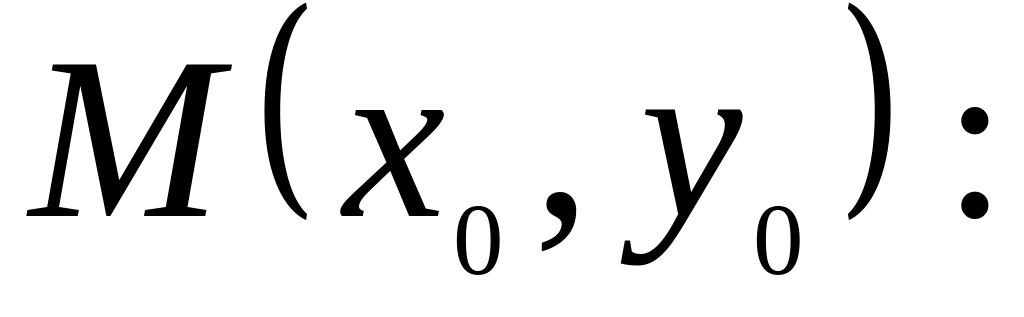
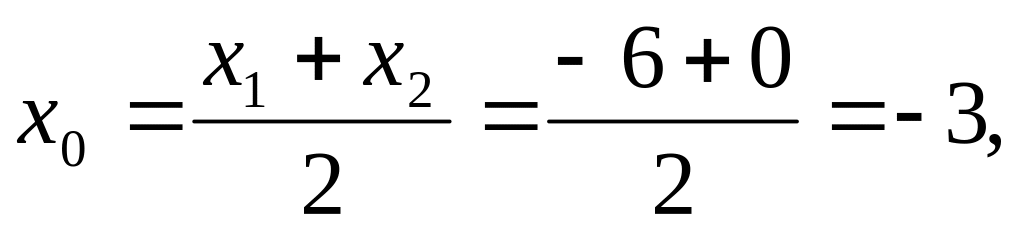
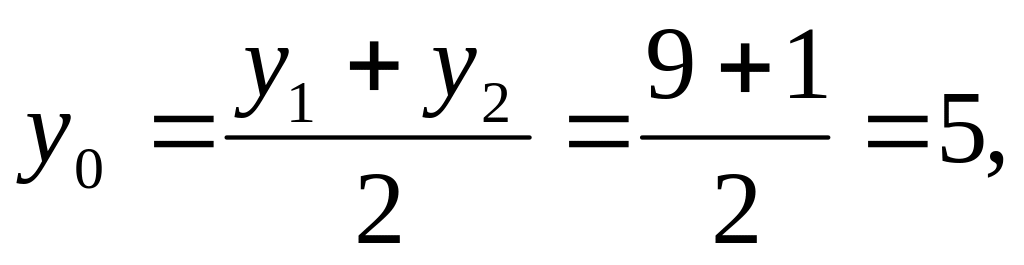координаты
М(-3,5);угловой коэффициент прямой AF:
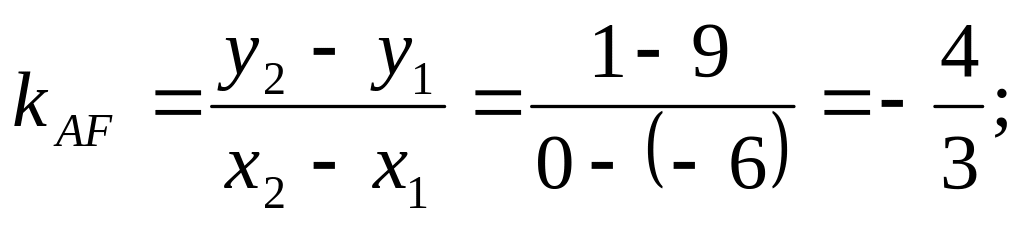
угловой коэффициент перпендикуляра к AF равен:
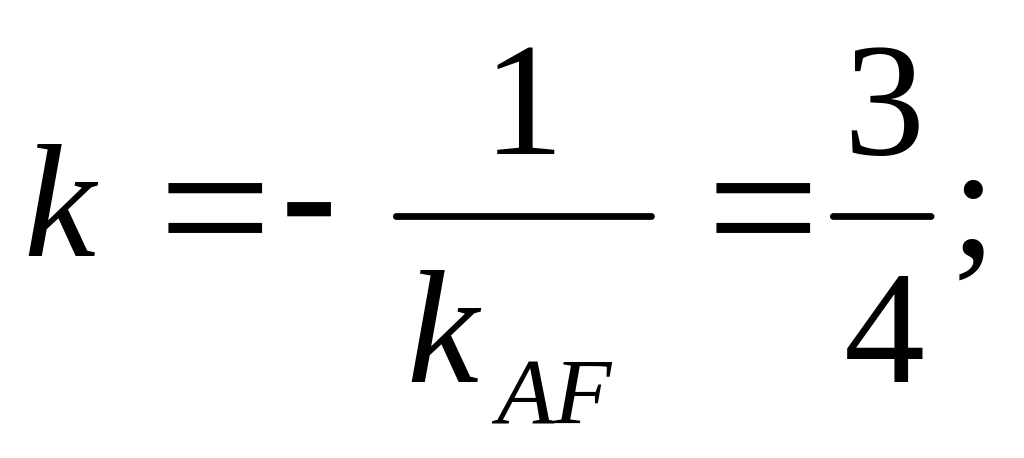
по формуле
составим уравнение искомого перпендикуляра,
проходящего через точку М(-3,5):
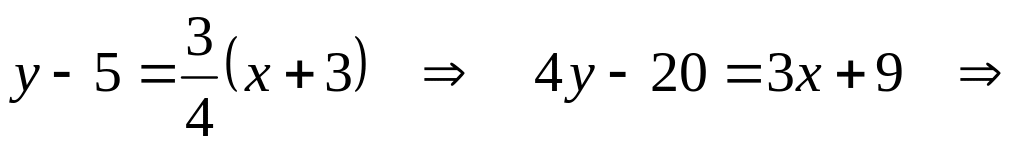3х-4у+29=0.
Задача 39.
Построить
параболу
Задача 40.
Построить параболы:
Найти координаты их фокусов.